STL容器：set、multiset的简介与使用

最新推荐文章于 2024-10-19 11:35:01 发布
最新推荐文章于 2024-10-19 11:35:01 发布
阅读量493 收藏 2
点赞数 1
分类专栏： STL 文章标签： STL C++
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/weixin_43690795/article/details/107339309
版权
本文深入探讨了C++标准模板库(STL)中set和multiset容器的特性和使用方法。从数据结构原理到具体应用，包括红黑树实现、元素插入查找、迭代器操作等，为读者提供了全面的指导。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

set的介绍

  1. set是按照一定次序存储元素的容器
  2. 在set中，元素的value也标识它(value就是key，类型为T)，并且每个value必须是唯一的。set中的元素不能在容器中修改(元素总是const)，但是可以从容器中插入或删除它们
  3. 在内部，set中的元素总是按照其内部比较对象(类型比较)所指示的特定严格弱排序准则进行排序
  4. set容器通过key访问单个元素的速度通常比unordered_set容器慢，但它们允许根据顺序对子集进行直接迭代
  5. set在底层是用平衡搜索树(红黑树)实现的
  6. 使用set时必须加上头文件#include<set>和using namespace std;

注意：

  1. 与map/multimap不同，map/multimap中存储的是真正的键值对<key, value>，set中只放value，但在底层实际存放的是由<value, value>构成的键值对
  2. set中插入元素时，只需要插入value即可，不需要构造键值对
  3. set中的元素不可以重复(因此可以使用set进行去重)
  4. 使用set的迭代器遍历set中的元素，可以得到有序序列
  5. set中的元素默认按照小于来比较
  6. set中查找某个元素，时间复杂度为：O(log2N)
  7. set中的元素不允许修改
  8. set中的底层使用红黑树来实现

set的使用

1.set的模板参数列表
在这里插入图片描述
T: set中存放元素的类型，实际在底层存储<value, value>的键值对
Compare：set中元素默认按照小于来比较
Alloc：set中元素空间的管理方式，使用STL提供的空间配置器管理

2.set的构造

函数声明功能介绍
set (const Compare& comp = Compare(), const Allocator& = Allocator() );构造空的set
set (InputIterator first, InputIterator last, const Compare& comp = Compare(), const Allocator& = Allocator() );用[first, last)区间中的元素构造set
set ( const set<Key,Compare,Allocator>& x);set的拷贝构造

3.常见的set的迭代器

函数声明功能介绍
iterator begin()返回set中起始位置元素的迭代器
iterator end()返回set中最后一个元素后面的迭代器
const_iterator cbegin() const返回set中起始位置元素的const迭代器
const_iterator cend() const返回set中最后一个元素后面的const迭代器
reverse_iterator rbegin()返回指向容器中最后一个元素的反向迭代器
reverse_iterator rend()返回一个反向迭代器，该反向迭代器指向set容器中第一个元素之前的理论元素

4.set的容量

函数声明功能介绍
bool empty ( ) const检测set是否为空，空返回true，否则返回true
size_type size() const返回set中有效元素的个数

5.set的修改操作

函数声明功能介绍
pair<iterator,bool> insert (const value_type& val);在set中插入元素x，实际插入的是<x, x>构成的键值对，如果插入成功，返回<该元素在set中的位置，true>,如果插入失败，说明x在set中已经存在，返回<x在set中的位置，false>
void erase (iterator position)删除set中position位置上的元素
size_type erase ( const key_type& x )删除set中值为x的元素，返回删除的元素的个数
void erase ( iterator first, iterator last )删除set中[first, last)区间中的元素
void swap (set<Key, Compare, Allocator>& st );交换set中的元素
void clear ( )将set中的元素清空
iterator find (const key_type& x) const返回set中值为x的元素的位置
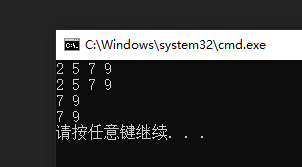
void Test()
{
	//排序+去重
	set<int> s;
	s.insert(9);
	s.insert(5);
	s.insert(2);
	s.insert(7);
	s.insert(5);
	for (auto e : s)
	{
		cout << e << " ";
	}
	cout << endl;

	set<int>::iterator it = s.begin();
	while (it != s.end())
	{
		cout << *it << " ";
		++it;
	}
	cout << endl;

	auto pos = s.find(5);
	if (pos != s.end())
	{
		s.erase(pos);
	}
	s.erase(2);
	for (auto e : s)
	{
		cout << e << " ";
	}
	cout << endl;

	set<int> copy(s);
	for (auto e : copy)
	{
		cout << e << " ";
	}
	cout << endl;
}

在这里插入图片描述

multiset的介绍

  1. multiset是按照特定顺序存储元素的容器，其中元素是可以重复的。
  2. 在multiset中，元素的value也会识别它(因为multiset中本身存储的就是<value, value>组成的键值对，因此value本身就是key，key就是value，类型为T). multiset元素的值不能在容器中进行修改(因为元素总是const的)，但可以从容器中插入或删除。
  3. 在内部，multiset中的元素总是按照其内部比较规则(类型比较)所指示的特定严格弱排序准则进行排序。
  4. multiset容器通过key访问单个元素的速度通常比unordered_multiset容器慢，但当使用迭代器遍历时会得到一个有序序列。
  5. multiset底层结构为平衡搜索树(红黑树)。

注意：

  1. multiset中在底层中存储的是<value, value>的键值对
  2. mtltiset的插入接口中只需要插入即可
  3. 与set的区别是，multiset中的元素可以重复，set是中value是唯一的
  4. 使用迭代器对multiset中的元素进行遍历，可以得到有序的序列
  5. multiset中的元素不能修改
  6. 在multiset中找某个元素，时间复杂度为O(log2N)
  7. multiset的作用：可以对元素进行排序
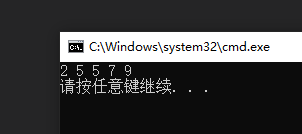
void Test()
{
	multiset<int> ms;
	ms.insert(9);
	ms.insert(5);
	ms.insert(5);
	ms.insert(2);
	ms.insert(7);
	for (auto& e : ms)
	{
		cout << e << " ";
	}
	cout << endl;
}

在这里插入图片描述

set的模拟实现（红黑树实现）

#pragma once
#include <iostream>
using namespace std;

//节点的颜色
enum Color
{
	RED,
	BLACK
};

template<class T>
struct RBTreeNode
{
	RBTreeNode<T>* _left;  //左孩子
	RBTreeNode<T>* _right; //右孩子
	RBTreeNode<T>* _parent;//双亲
	T _data;
	Color _col; //红黑颜色限制, 新插入节点默认为红色
	RBTreeNode(const T& data, Color col = RED)
		: _left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		, _data(data)
		, _col(col)
	{}
};

template<class T, class Ref, class Ptr>
struct RBTreeIterator
{
	typedef RBTreeIterator<T, Ref, Ptr> Self;
	typedef RBTreeNode<T> Node;
	Node* _node;
	RBTreeIterator(Node* node)
		: _node(node)
	{}

	Ref operator*()
	{
		return _node->_data;
	}

	Ptr operator->()
	{
		return &_node->_data;
	}

	Self& operator++()
	{
		if (_node->_right)
		{
			Node* subLeft = _node->_right;
			while (subLeft->_left)
			{
				subLeft = subLeft->_left;
			}
			_node = subLeft;
		}
		else
		{
			Node* cur = _node;
			Node* parent = cur->_parent;
			while (parent && cur == parent->_right)
			{
				cur = cur->_parent;
				parent = cur->_parent;
			}
			_node = parent;
		}
		return *this;
	}

	bool operator!=(const Self& s)
	{
		return _node != s._node;
	}
};


template<class K, class T, class KOfT>
class RBTree
{
	typedef RBTreeNode<T> Node;
public:
	typedef RBTreeIterator<T, T&, T*> iterator;
	typedef RBTreeIterator<T, const T&, const T*> const_iterator;

	iterator begin()
	{
		Node* cur = _root;
		while (cur && cur->_left)
		{
			cur = cur->_left;
		}
		return iterator(cur);
	}

	iterator end()
	{
		return nullptr;
	}
public:
	pair<iterator, bool> Insert(const T& data)
	{
		if (_root == nullptr)
		{
			_root = new Node(data);
			_root->_col = BLACK;
			return make_pair(iterator(_root), true);
		}

		KOfT koft;
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (koft(data) > koft(cur->_data))
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (koft(data) < koft(cur->_data))
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				return make_pair(iterator(cur), false);
			}
		}

		cur = new Node(data);
		Node* newNode = cur;
		cur->_col = RED;
		if (koft(data) > koft(parent->_data))
		{
			parent->_right = cur;
			cur->_parent = parent;
		}
		else
		{
			parent->_left = cur;
			cur->_parent = parent;
		}

		//检测红黑树的性质
		while (parent && parent->_col == RED)
		{
			Node* grandfather = parent->_parent;
			if (parent == grandfather->_left)
			{
				Node* uncle = grandfather->_right;
				//情况一：uncle存在且为红
				if (uncle && uncle->_col == RED)
				{
					parent->_col = uncle->_col = BLACK;
					grandfather->_col = RED;

					//继续向上调整
					cur = grandfather;
					parent = cur->_parent;
				}
				else //情况二/三：uncle不存在或uncle存在且为黑
				{
					//情况三双旋后变单旋，成为情况二
					if (cur == parent->_right)
					{
						RotateL(parent);
						//交换的是节点的指针，不是节点
						swap(cur, parent);
					}

					//处理情况二
					RotateR(grandfather);
					grandfather->_col = RED;
					parent->_col = BLACK;

					//调整结束
					break;
				}
			}
			else //parent == grandfather->_right
			{
				Node* uncle = grandfather->_left;
				if (uncle && uncle->_col == RED)
				{
					parent->_col = uncle->_col = BLACK;
					grandfather->_col = RED;

					cur = grandfather;
					parent = cur->_parent;
				}
				else
				{
					if (cur == parent->_left)
					{
						RotateR(parent);
						swap(cur, parent);
					}

					RotateL(grandfather);
					grandfather->_col = RED;
					parent->_col = BLACK;

					break;
				}
			}
		}
		_root->_col = BLACK;
		return make_pair(iterator(newNode), true);;
	}

	iterator Find(const K& key)
	{
		KOfT koft;
		Node* cur = _root;
		while (cur)
		{
			if (key > koft(cur->_data))
			{
				cur = cur->_right;
			}
			else if (key < koft(cur->_data))
			{
				cur = cur->_left;
			}
			else
			{
				return iterator(cur);
			}
		}
		return iterator(nullptr);
	}
private:
	//左单旋
	void RotateL(Node* parent)
	{
		Node* pParent = parent->_parent;
		Node* subR = parent->_right;
		Node* subRL = subR->_left;

		parent->_right = subRL;
		if (subRL)
		{
			subRL->_parent = parent;
		}

		subR->_left = parent;
		parent->_parent = subR;

		if (_root == parent)
		{
			_root = subR;
			subR->_parent = nullptr;
		}
		else
		{
			if (parent == pParent->_left)
			{
				pParent->_left = subR;
			}
			else
			{
				pParent->_right = subR;
			}
			subR->_parent = pParent;
		}
	}

	//右单旋
	void RotateR(Node* parent)
	{
		Node* pParent = parent->_parent;
		Node* subL = parent->_left;
		Node* subLR = subL->_right;

		parent->_left = subLR;
		if (subLR)
		{
			subLR->_parent = parent;
		}

		subL->_right = parent;
		parent->_parent = subL;

		if (_root == parent)
		{
			_root = subL;
			subL->_parent = nullptr;
		}
		else
		{
			if (parent == pParent->_left)
			{
				pParent->_left = subL;
			}
			else
			{
				pParent->_right = subL;
			}
			subL->_parent = pParent;
		}
	}
private:
	Node* _root = nullptr;
};

namespace Set
{
	template<class K>
	class set
	{
		struct SetKeyOfT
		{
			const K& operator()(const K& key)
			{
				return key;
			}
		};
	public:
		typedef typename RBTree<K, K, SetKeyOfT>::iterator iterator;

		iterator begin()
		{
			return _t.begin();
		}

		iterator end()
		{
			return _t.end();
		}
	public:
		pair<iterator, bool> Insert(const K& key)
		{
			return _t.Insert(key);
		}

		iterator Find(const K& key)
		{
			return _t.Find(key);
		}
	private:
		RBTree<K, K, SetKeyOfT> _t;
	};

	void TestSet()
	{
		set<int> s;
		s.Insert(3);
		s.Insert(4);
		s.Insert(1);
		s.Insert(2);
		s.Insert(5);

		set<int>::iterator it = s.begin();
		while (it != s.end())
		{
			cout << *it << " ";
			++it;
		}
		cout << endl;

		for (auto e : s)
		{
			cout << e << " ";
		}
		cout << endl;

		set<int>::iterator pos = s.Find(3);
		if (pos != s.end())
		{
			cout << *pos << endl;
		}
	}
}
一篇搞懂C++ STL 关联容器std::multiset
m0_62599305的博客
08-30 1305
在C++标准模板库（STL）中，是一种重要的关联容器，用于存储有序的元素，并允许重复元素的存在。它适用于需要维护元素顺序且需要存储重复元素的场景。和std::set都基于红黑树（通常的实现方式）来存储元素，确保元素的有序性以及高效的查找、插入和删除操作。理解这两者的区别和用途对选择合适的容器至关重要。是一个有序的关联容器，它能够存储多个具有相同键值的元素。与std::set不同，允许在集合中存在重复的元素。每个元素都被自动排序，保证了容器的有序性。元素有序：元素会根据指定的比较函数进行排序，默认是升序。
std::set与std::multiset使用总结
大山喵写博客的地方
11-04 5938
Set和Multiset Set和Multiset的能力 Set和Multiset的操作函数 创建、复制和析构函数 非更易型操作(Nonmodifying Operating) 特殊的查找函数 赋值(Assignment) 迭代器函数(Iterator Function) 插入和移除(Inserting and Removing) 异常处理 　　 ...
STL之multiset简介
weixin_33915554的博客
09-27 322
2019独角兽企业重金招聘Python工程师标准>>> ...
multiset
03-26 167
使用multiset，和set一样可以自动排序，不同点在于multiset中可以有重复的元素 a.find(elem) 返回元素值为elem的第一个元素的迭代器，如果没有返回end() a.erase(pos) 移除迭代器pos所指位置元素，无返回值 (a.erase(elem) 删除与elem相等的所有元素，返回被移除的元素个数) a.begin() 返回一个迭代器，...
STL之Multiset
CillyB的博客
06-28 474
Multiset的中文名是多重集合，其实就是集合的扩展版。唯一的不同是集合中一个值只能出现一次，而多重集合中一个值可以出现多次。   　　粗略看了看MSDN，在STL中，multiset和set的成员函数声明也是基本一样的，一些需要注意的地方是： set::insert(key)的返回值是一个pair，其中pair中的bool成员表明了key被插入之前，set中是否已存在相同
STLset容器大小和交换
码云仓库地址：https://gitee.com/lance-gyq
03-10 227
STLset容器大小和交换 功能描述： 统计set容器大小以及交换set容器 函数原型： size(); //返回容器中元素的数目 empty(); //判断容器是否为空 swap(st); //交换两个集合容器 代码示例： #include<iostream> #include<set> using namespace std; void printSet(set<int>&s) { for (set<int
STL：set与multiset容器详解及应用
本篇内容主要介绍了C++标准模板库（Standard Template Library，简称STL）中的两种容器：集合（set）和多元集合（multiset）。STL是C++中最核心的部分之一，它提供了丰富的数据结构、算法、迭代器、函数对象和内存...
【C++中STL】set/multiset容器
qq_50563459的博客
01-26 596
在使用仿函数排序时，需要加const不可修改，不然会报错，set的排序规则下定义是需要设置好，默认是升序。查找key是否存在，若存在，返回该键的元素的迭代器，若不存在，返回set.end()set不允许容器中有重复的元素，multiset允许容器中有重复的元素。删除迭代器从beg到end之间的元素，返回下一个数据的位置。2、set插入数据的同时会返回插入结果，表示插入成功。1、set不可以插入重复数据，multiset可以。删除pos位置的元素，返回下一个数据的位置。返回容器中元素的个数。
C++ STL系列容器（六）：树形结构的关联式容器（map、set、multimap、multiset）
rab1211764820的博客
04-07 1417
树形结构的关联式容器（map、set、multimap、multiset） 关联式容器 键值对 map、set的相关OJ：两个数组的交集、前k个高频单词、单词识别
C++：map与set简析
qq_62718027的博客
08-05 2230
举例：我插入1-5,7,9.然后用lower_bound找3和6,3可以直接找到，但是6没有，所以返回>=6最近的元素7.set 翻译为集合，是一个内部自动有序且不含重复元素的容器，加入 set 之后可以实现自动排序。如果我们判断了，没有这个数再进行删除，那么就不会报错了，所以说判断是很重要的不能省略。此时虽然队列中有3，但是upper是返回比3更大值的最近的一个，所以返回了4。算法中的find是暴力查找，是遍历整个区间，所以时间复杂度是O（N）；map是STL的一个关联容器，它提供一对一的hash。...
multiset的介绍及使用
gp1330782530的博客
05-28 1万+
multiset的介绍及使用 1、multiset的介绍 1、multiset是按照特定顺序存储元素的容器，其中元素是可以重复的 2、在multiset在，元素的value也会识别它组成的键值对，multiset元素的值不能在容器中进行修改，但可以插入和删除 3、在内部，multiset按照特定的严格弱排序准则进行排序 4、multiset容器通过key访问单个元素比unordered_multiset容器慢，但当使用迭代器遍历的时候，会得到一个有序序列 5、multiset的底层是二叉搜索树（红黑树）
【C++】map、set，multiset和multimap的使用及底层原理【完整版】
m0_74044018的博客
09-30 1080
c++中map、set，multiset和multimap的使用及其底层原理，附一道利用map和multimap求解的OJ题
【C++】Set/Multiset和Map/Multimap的了解使用
最新发布
2301_81577798的博客
10-19 1068
初识set和map
【转】C++ STL中常见容器的时间复杂度
weixin_30751947的博客
09-21 2048
map, set, multimap, and multiset 上述四种容器采用红黑树实现，红黑树是平衡二叉树的一种。不同操作的时间复杂度近似为: 插入: O(logN) 查看:O(logN) 删除:O(logN) hash_map, hash_set, hash_multimap, and hash_multiset 上述四种容器采用哈希表实现，不同操作的时间复杂度为：...
C++ STL中常见容器的时间复杂度
wusecaiyun的专栏
07-02 4万+
map, set, multimap, and multiset 上述四种容器采用红黑树实现，红黑树是平衡二叉树的一种。不同操作的时间复杂度近似为: 插入: O(logN) 查看:O(logN) 删除:O(logN) hash_map, hash_set, hash_multimap, and hash_multiset 上述四种容器采用哈希表实现，不同操作的时间复杂度为：
multiset用法总结
热门推荐
二喵君的博客
12-04 12万+
       c++语言中，multiset是&lt;set&gt;库中一个非常有用的类型，它可以看成一个序列，插入一个数，删除一个数都能够在O(logn)的时间内完成，而且他能时刻保证序列中的数是有序的，而且序列中可以存在重复的数。 简单应用： 通过一个程序来看如何使用multiset： #include &lt;string&gt; #include &lt;iostream&gt; ...
STL学习笔记— —容器set和multiset
Sin_Geek成长の迹
04-08 3721
简介在头文件<setr> 中定义namespace std { template <typename T, typename Compare = less<T>, typename Allocator = allocator<T> > class set; template <typename T,
滑动窗口 单调队列或者multiset
lt的博客
05-06 284
题目链接 https://www.acwing.com/problem/content/156/ 题目 给定一个大小为n≤10^6的数组。 有一个大小为k的滑动窗口，它从数组的最左边移动到最右边。 您只能在窗口中看到k个数字。 每次滑动窗口向右移动一个位置。 以下是一个例子： 该数组为[1 3 -1 -3 5 3 6 7]，k为3。 窗口位置 最小值 最大值 [1...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值