计算机视觉：2.3.1、梯度下降法优化权重矩阵

二、优化方法和正则方法

“Nearly all of deep learning is powered by one import algorithm :Stochastic Gradient Descent(SGD)” —Goodfellow et al.

·几乎所有深度学习都是被一种重要的算法所驱动的：随机梯度下降算法。

​ 我们现在已经知道，想要得到一个高准确率的分类器，主要取决于找到一系列的权重W和b，只有这样我们的样本点才能被正确的分类。

​ 但是问题就在于：我们如何能够找到能使分类器准确分类的 W和 b呢？

​ 首先我们会想到：暴力破解。

​ 对于计算机来说，我们可以通过不断生成随机数，然后评估此次分类的准确率，重复此步骤，直到找到我们满意的结果为止。

​ 但是，就现代而言，稍微复杂一点的模型中包含的参数就可能有百万甚至千万个，如果我们只是靠碰运气，很可能几个月甚至几年也很难达到我们想要的结果。

​

​ 所以我们应该定义一种优化算法，能够让我们逐步地、实实在在地提升分类器的效果，也就是找到比上一次更好的W和b, 于是人们提出了梯度下降算法：

​ 总的来说，不管是梯度下降算法还是其变体，其中心思想都可以总结为：

​ 迭代地评估参数，计算损失，然后朝着能够减小损失地方向前进一小步

​ 梯度计算公式：
$$\frac{df(x)}{dx}=li{m}_{x->0}\frac{f(x+h)-f(x)}{h}$$
​ 当维度大于1时，梯度变成了偏导数地向量。这个等式存在如下问题：

1. 是导数地近似值。

2. 计算起来很慢

   实际上，我们通过 分析梯度 来代替之，这种方法又快又准确。

​ 上面所讲， 我们是将问题简化为凸曲面问题来就行计算了，比如说我们将随机参数地取值范围看作是一个碗上面地的所有点，我们刚开始的时候随机站在碗的一处，我们将梯度方向作为我们前进的方向，最终我们将到达我们的目的地—碗底，也就是问题中 损失最小的参数点。

​ 但在实际的问题中，我们所面临的并非是如此理想化的场景，我们需要面对的不是一个规则的凸曲面，而是一个坑坑洼洼，时而尖峰时而低谷甚至还有可能出现断裂的不规则曲线，那么我们还能够这样处理问题吗？

​ 答案是肯定的，因为它足够简单。

​ 在这里我们再次引用Goodfellow的一句话：

“[An] optimization algotrithm may not be guaranteed to arrive at even a local minimum in a reasonable amount of time ,but it often finds a very low value of the [loss] quickly enough to be useful ”

​ 即，虽然这个优化算法甚至都无法保证在合理时间内达到一个局部最小值，但它通常能极快的找到一个有用的低损失值

简而言之：性价比极高，且效果够用！

小技巧：将b向量（截距项）隐藏在W矩阵（权重）矩阵中进行学习

我们只需要在输入数据的每一行后加一项：1，然后初始化权重矩阵W的时候，多加一行即可，可以自己试试看，运算结果是完全相同的。

这样我们就将截距项藏于权重矩阵治之中，不用再单独进行管理了。

代码实现：

from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
import numpy as np


def sigmoid_activation(x):
    return 1.0 / (1 + np.exp(-x))


def predict(X, W):
    preds = sigmoid_activation(X.dot(W))
    preds[preds <= 0.5] = 0
    preds[preds > 0] = 1
    return preds


(X, y) = make_blobs(n_samples=1000, n_features=2, centers=2, cluster_std=1.5, random_state=1)
y = y.reshape((y.shape[0], 1))

X = np.c_[X, np.ones((X.shape[0]))]

(trainX, testX, trainY, testY) = train_test_split(X, y, test_size=0.5, random_state=42)

print("[INFO] training....")
W = np.random.randn(X.shape[1], 1)
losses = []

for epoch in np.arange(0, 100):
    preds = sigmoid_activation(trainX.dot(W))
    error = preds - trainY
    loss = np.sum(error ** 2)
    losses.append(loss)

    gradient = trainX.T.dot(error)

    W += -0.01 * gradient

    if epoch == 0 or (epoch + 1) % 5 == 0:
        print("[INFO] epoch={}, loss={:.7f}".format(int(epoch + 1), loss))

print("[INFO] evaluating....")

preds = predict(testX, W)
print(classification_report(testY, preds))

plt.style.use("ggplot")
plt.figure()
plt.title("Data")
plt.scatter(testX[:, 0], testX[:, 1], marker="o", c=testY, s=30)

plt.style.use("ggplot")
plt.figure()
plt.plot(np.arange(0, 100), losses)
plt.title("Training Loss")
plt.xlabel("Epoch")
plt.ylabel("Loss")
plt.show()

上述的代码首先从make_blobs中制造了数据集，这个数据集中又两类数据，每类数据有1000个样本点，每个样本点有2个特征，我们将其按照1：1的比例划分为训练集和测试集，然后通过梯度下降算法对模型的权重矩阵W进行优化，并对测试集进行分类，将最终的分类结果输出。

代码运行结果：

E:\DLstudy\Scripts\python.exe E:/PycharmProjects/DLstudy/run/gradient_descent.py
[INFO] training....
[INFO] epoch=1, loss=234.7830329
[INFO] epoch=5, loss=3.1560888
[INFO] epoch=10, loss=1.3547706
[INFO] epoch=15, loss=0.6473488
[INFO] epoch=20, loss=0.3511611
[INFO] epoch=25, loss=0.2398222
[INFO] epoch=30, loss=0.1882352
[INFO] epoch=35, loss=0.1586320
[INFO] epoch=40, loss=0.1389283
[INFO] epoch=45, loss=0.1244876
[INFO] epoch=50, loss=0.1132147
[INFO] epoch=55, loss=0.1040314
[INFO] epoch=60, loss=0.0963231
[INFO] epoch=65, loss=0.0897106
[INFO] epoch=70, loss=0.0839443
[INFO] epoch=75, loss=0.0788517
[INFO] epoch=80, loss=0.0743083
[INFO] epoch=85, loss=0.0702213
[INFO] epoch=90, loss=0.0665198
[INFO] epoch=95, loss=0.0631480
[INFO] epoch=100, loss=0.0600613
[INFO] evaluating....
              precision    recall  f1-score   support

           0       1.00      0.99      1.00       250
           1       0.99      1.00      1.00       250

    accuracy                           1.00       500
   macro avg       1.00      1.00      1.00       500
weighted avg       1.00      1.00      1.00       500

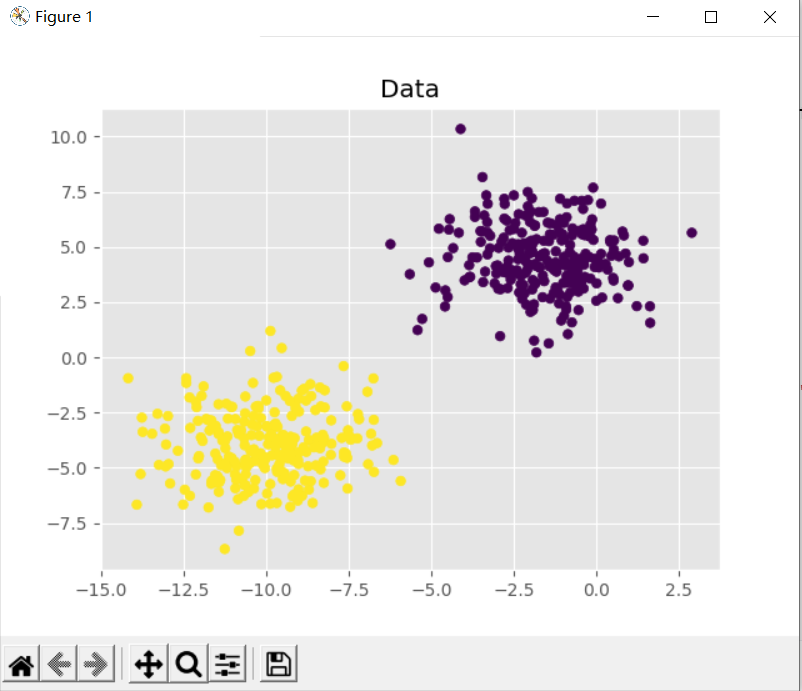
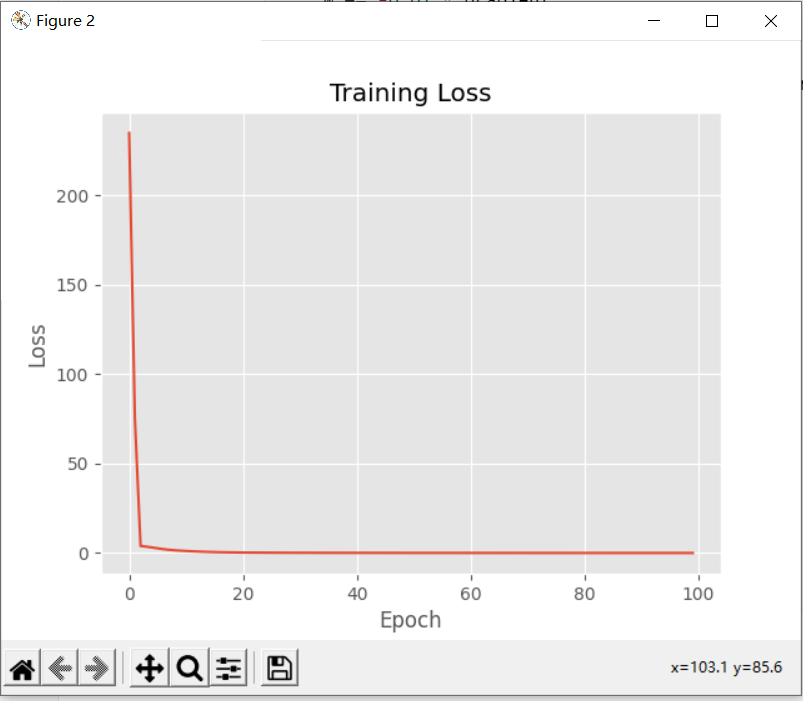
​ 从结果可以看出，类别0的分类100%正确，但是类别1的正确率却只有99%，造成这种差异的原因重要在于经典梯度下降算法每个epoch只更新一次权重矩阵W，在上述代码的100个epoch中，也就只更新了100次W，所以很有可能还没有学习到能将两类样本点分开的直线，算法就停止了。