数据结构

最新推荐文章于 2024-09-02 21:43:34 发布

梦想阳光早晨

最新推荐文章于 2024-09-02 21:43:34 发布

阅读量549

点赞数

CC 4.0 BY-SA版权

本文链接：https://blog.youkuaiyun.com/weixin_43614024/article/details/104126095

在进行函数实现的时候，主要考虑 函数类型 (是否为常量函数)、 返回值类型 和 参数类型(传值参数、引用参数、常量引用参数)。

16-单链表小结

23-栈和队列

1. 栈(stack)

是 线性表 的一种具体形式，在线性表的基础上加了一些限制。

栈：先进后出；
只在表尾进行删除(pop)和插入(push)操作；
表尾称为栈顶(top)，表头称为栈底(bottom)；

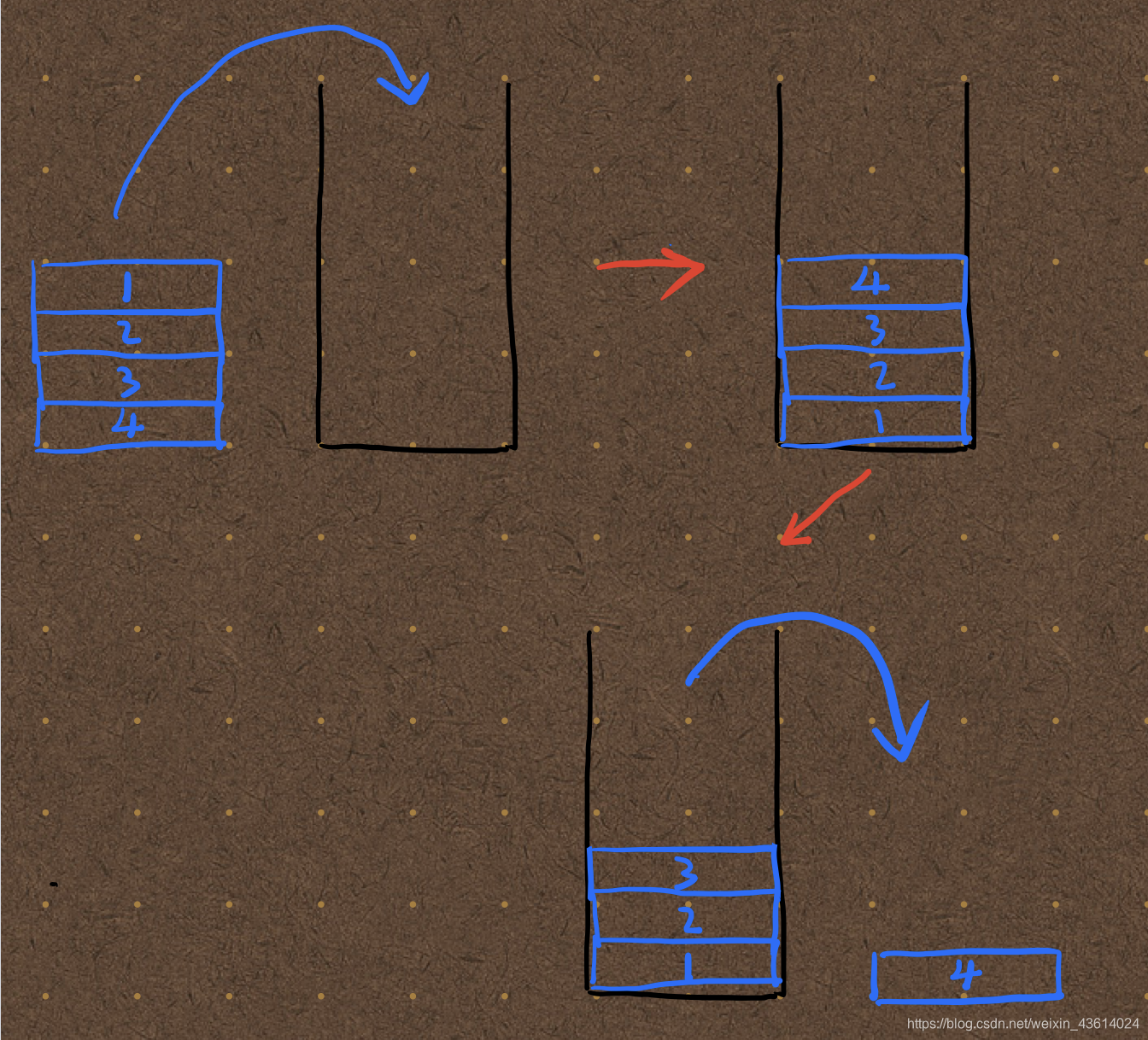
如下图所示，1、2、3、4四个木块依次放入桶中，首先放入的1号木块会位于桶底，最后放入的4号木块会位于最上面，取出时，后放入的木块会先取出。
在这里插入图片描述
栈的一些使用实例，例如浏览器的网页“回退”功能，从最后打开的网页依次退出；Word等软件的撤销功能等。

2. 队列(queue)

与栈一样，也是 线性表 的一种具体形式，在线性表的基础上加了一些限制。

队列：先进先出；
只允许在一端进行删除操作，而在另一端进行插入操作；

3. 递归

递归效率比较低，除非没有办法，一般用迭代代替(已知迭代次数)

4. 分治

5. 汉诺塔问题

汉诺塔(Tower of Hanoi)源于印度传说中，大梵天创造世界时造了三根金钢石柱子，
其中一根柱子自底向上叠着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始
按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，
在三根柱子之间一次只能移动一个圆盘。

汉诺塔问题的巧妙之处在于最大的圆盘可以视若无睹，因为它的存在不影响其它圆盘的移动，
谁都可以放它上面，所以64个圆盘的移动可以首先完成63个圆盘的移动，63个圆盘的移动可
以首先完成62个圆盘的移动，以此类推，3个圆盘的移动可以先实现2个圆盘的移动。
我们来计算一下需要多少步：
将64个圆盘完全移动到另一根柱子上，可以分三部分，第一部分先将63个圆盘移动到柱2，再
将第64个圆盘移动到柱3，再将63个圆盘移动到第64个圆盘上，
64个圆盘移动的次数记为 count(64)，根据分析可得：
count(64)=count(63)*2+1;
count(63)=count(62)*2+1;
count(62)=count(61)*2+1;
……
count(2)=count(1)*2+1;
count(1)=1;

我们计算了汉诺塔的移动次数，但我们实际上是要编程实现怎么移动的，(哭脸)，
1、仅输出移动的步骤，而不关心每次移动后每根柱子上的圆盘状态，简单的递归就可以实现

转载C语言实现汉诺塔

那么程序是怎么来的呢？
我们可以自己手动解决一个简单的汉诺塔问题，在推导过程中结合之前计算步骤时的分析便
可发现这样的规律：

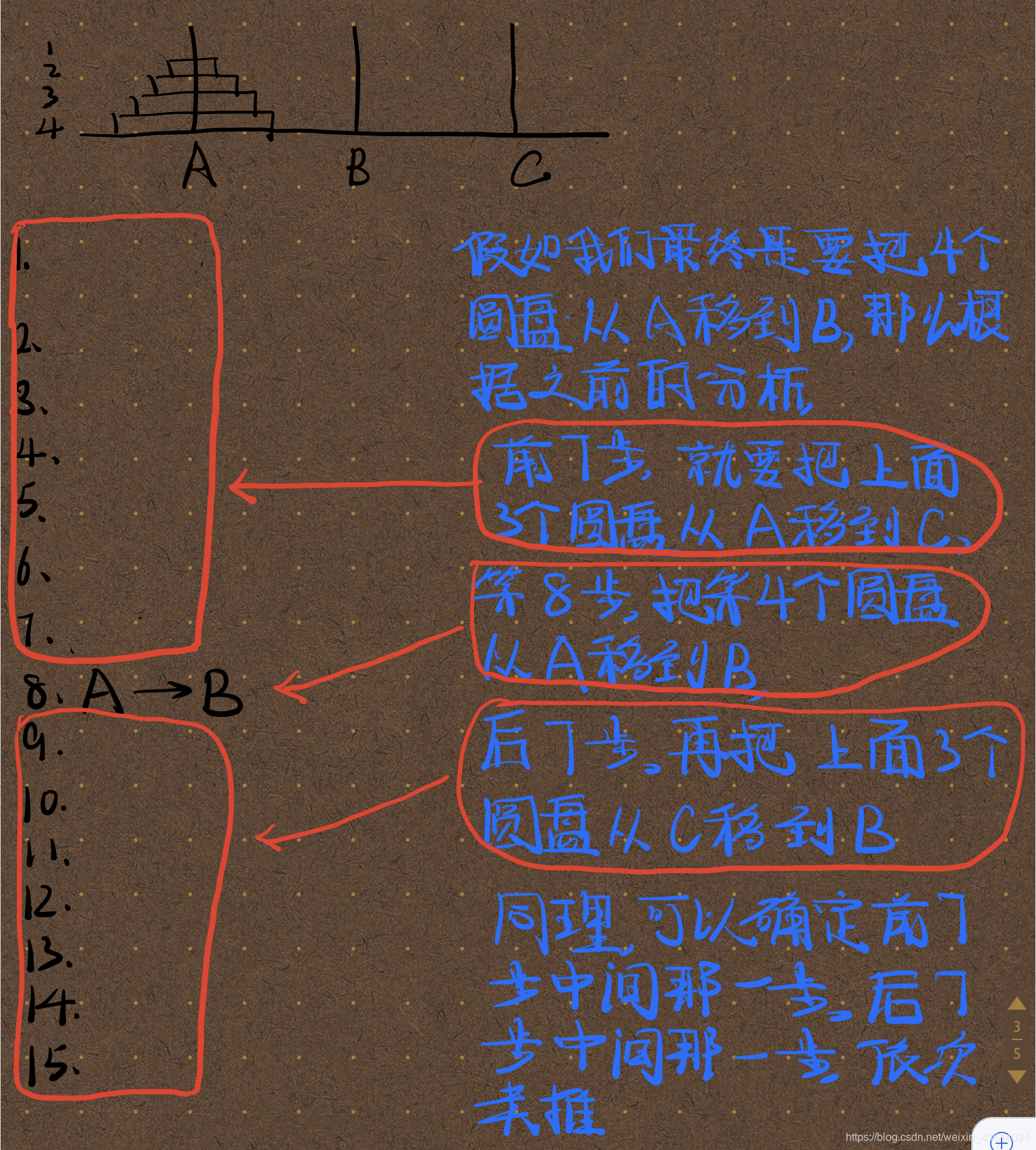
在这里插入图片描述

每次确定中间那一步，依次回溯，我们可以不用图解，就可以直接写出给定数量圆盘的所有步
骤，我们还是以4个圆盘为例，
///第一次分析
hannuo(4,A,B,C) //表示把4个圆盘从A移动到B,分为3步
hannuo(3,A,C,B) //第一步，把3个圆盘从A移动到C
move(A,B)           //第二步，把第四个圆盘从A移动到B
hannuo(3,C,B,A) //第三步，把3个圆盘从C移动到B

///第二次分析
hannuo(3,A,C,B) //把3个圆盘从A移动到C，也分为3步
hannuo(2,A,B,C) //第一步，把2个圆盘从A移动到B
move(A,C)           //第二步，把第3个圆盘从A移动到C
hannuo(3,B,C,A) //第三步，把2个圆盘从B移动到C

发现规律了吧，这样就可以递归啦
hannuo(n,one,two,three)  //移动n个圆盘从one到two，当然也可以到three，这里以two为例
{
	hannuo(n-1,one,three,two);
	move(one,two);
	hannuo(n-1,three,two,one);
}

最后别忘了加上递归的终止条件
hannuo(n,one,two,three)  //移动n个圆盘从one到two，当然也可以到three，这里以two为例
{
        if(n==1){
           move(one,two);
        }
 	hannuo(n-1,one,three,two);
 	move(one,two);
 	hannuo(n-1,three,two,one);
}

2、不仅输出移动的步骤，而且关心每次移动后每根柱子上的圆盘状态
这个就可以用栈啦，每个柱子就是一个栈，
move(A,B) 就是取出A栈的栈顶元素放入B栈中

6. 八皇后问题

八皇后问题，是一个古老而著名的问题，是回溯算法的典型案例。该问题是国际西洋棋棋手马
克斯·贝瑟尔于1848年提出：在8×8格的国际象棋上摆放八个皇后，使其不能互相攻击，即任
意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。 高斯认为有76种方
案。1854年在柏林的象棋杂志上不同的作者发表了40种不同的解，后来有人用图论的方法解
出92种结果。

八皇后问题的算法实现与我们手解的思路相同，只不过计算机加速了这个过程
1. 从棋盘的第一行第一个位置开始，依次判断当前位置是否能够放置皇后，可以就放置，
不可以的话接着检验下一个位置
3. 如果某行所有位置都不符合要求，则回溯到前一行，改变皇后的位置，继续尝试
4. 直到尝试到最后一行，求解完毕。

递归在八皇后问题中的使用，是因为每行的处理相同，处理完一行调用后再次调用函数处理
下一行

#include <stdio.h>
int count=0;

int notDanger(int row,int j,int (*chess)[8]){
    //判断列方向有没有危险
    for(int i=0;i<8;i++){
        if(*(*(chess+i)+j)!=0){
            return 0;
        }
    }
    //判断左上方有没有危险
    for(int i=row,k=j; i>=0 && k>=0;i--,k--){
        if(*(*(chess+i)+k)!=0){
            return 0;
        }
    }
    //判断左下方有没有危险
    for(int i=row,k=j; i<8 && k>=0;i++,k--){
        if(*(*(chess+i)+k)!=0){
            return 0;
        }
    }
    //判断右上方有没有危险
    for(int i=row,k=j; i>=0 && k<8;i--,k++){
        if(*(*(chess+i)+k)!=0){
            return 0;
        }
    }
    //判断右下方有没有危险
    for(int i=row,k=j; i<8 && k<8;i++,k++){
        if(*(*(chess+i)+k)!=0){
            return 0;
        }
    }
    return 1;
}

void EightQueen(int row, int n, int (*chess)[8] )
{
    ///进行每一行的判断前，使用的得是当前棋盘
    int chess2[8][8];
    for(int i=0;i<8;i++){
        for(int j=0;j<8;j++){
            chess2[i][j] = chess[i][j];
        }
    }
    //行数的编号是0-7
    if(row == 8){
        printf("第 %d 种\n", count+1);
        for(int i=0;i<8;i++){
            for(int j=0; j < 8; j++ ){
                printf("%d ", *(*(chess2+i)+j));
            }
            printf("\n");
        }
        printf("\n");
        count++;
    }else{
        for(int j=0;j<n;j++){
            if(notDanger(row,j,chess2)) // 判断是否危险
            {
                //给该行赋0的操作要有，因为可能处理过其他情况，该行的其他位置已经放置了棋子
                for(int i=0;i<8;i++){
                    *(*(chess2+row)+i) = 0;
                }
                *(*(chess2+row)+j) = 1;
                EightQueen(row+1,n,chess2);
            }
        }
    }
}


int main()
{
    ///棋盘初始化
    int chess[8][8]; //定义棋盘数组
    for(int i=0;i<8;i++){
        for(int j=0;j<8;j++){
            chess[i][j]=0; //初始化为0，表示各个位置都未放置棋子
        }
    }
    ///调用八皇后函数
    EightQueen(0,8,chess);
    printf("共有%d种方法\n\n",count);


    return 0;
}

36-字符串

数值工作–>非数值工作，诞生了字符串
子串与主串，例如，"lie"是”believe“的子串
字符串比较时，比较的是每个字符的ASCII码的大小
字符串的存储结构：顺序存储与链式存储
BF算法

BF算法，即暴力(Brute Force)算法，是普通的模式匹配算法，BF算法的目的是在主串S中找
到子串T。BF算法的思想就是将目标串S的第一个字符与模式串T的第一个字符进行匹配，若
相等，则继续比较S的第二个字符和 T的第二个字符；若不相等，则比较S的第二个字符和T
的第一个字符，依次比较下去，直到得出最后的匹配结果。

KMP算法

根据子串T的特征避免不必要的回溯，详细解释见 "小甲鱼数据结构与算法37集"

41-树

基本概念

结点：树是n个结点的有限集（n>=0）
根：非空树有且仅有一个根节点
子树：当n>1时，除根结点以外的其余结点可分为互不相交的有限集，其中每一个集合本身又是一棵树，称为根的子树
度：结点拥有的子树数称为结点的度，树的度取树内结点度的最大值
叶结点：度为0的结点称为叶节点，、
分支结点：度不为0的结点
内部结点：除根节点和叶结点外的其它结点
孩子，双亲，兄弟，祖先
深度：树的层数（根为第一层）
有序树，无序树
森林
树的存储结构(42集)：三种表示法，双亲表示法、孩子表示法、孩子兄弟表示法
双亲表示法： 双亲作为索引关键词。每个结点除了知道自己是谁，还知道双亲结点在哪里。所以找双亲很容易，但要找某个结点的孩子是谁，就要遍历整个树结构了。
**双亲表示法改进：**每个结点除了知道自己是谁，还知道双亲结点在哪里，自己的孩子在哪里。同理还可以添加左右兄弟关系。
**孩子表示法方案一：**根据树的度，声明足够的空间存放子树结点的指针。但十分浪费空间。
**孩子表示法方案二：**根据每个结点的度分配存放子树结点的指针。初始化和维护困难大。
**双亲孩子表示法：**每个结点都作为一个链表的头节点。依次链接他的孩子。并开辟一个空间指向他的双亲。

二叉树

左子树、右子树
满二叉树：所有分支结点都存在左子树和右子树，并且所有的叶子都在同一层上的二叉树
完全二叉树：对一棵具有n个结点的完全二叉树按层序编号，编号为 i 的结点与同样深度的满二叉树中编号为 i 的结点位置完全相同
二叉树的性质
二叉树的存储结构
顺序存储结构： 由于完全二叉树的结构特征，用一维数组存储二叉树中的各个结点，结点的存储位置能体现结点之间的逻辑关系。如果是一般的二叉树，可以增加不存在的结点改为完全二叉树。但对于右斜树，就比较浪费空间了。
链式存储结构： 因为二叉树最多有两个孩子，设计为一个数据域与两个指针域是比较自然的想法。这样的链表称为二叉链表。
二叉树的遍历：从根结点出发访问所有结点，每个结点仅且被访问一次。
根据根结点被访问的顺序，分为：
前序遍历： 先访问根结点，然后前序遍历左子树，再前序遍历右子树
中序遍历：
后序遍历：
层序遍历：
线索二叉树：定义为空的指针可以用来存储指向前驱后继的指针。但不是所有的结点都有两个空的指针域，所以增加两个标志，来说明究竟指向的是前驱后继，还是自己的孩子。