ResNet论文精读：翻译+学习笔记+Pytorch代码复现

智算学术

已于 2025-03-28 14:40:00 修改

阅读量1.3k

点赞数 17

CC 4.0 BY-SA版权

分类专栏：深度学习图像分类篇文章标签：深度学习卷积神经网络论文笔记机器学习神经网络人工智能 python

于 2025-03-13 15:49:51 首次发布

本文链接：https://blog.youkuaiyun.com/weixin_43576022/article/details/146232493

深度学习图像分类篇专栏收录该内容

14 篇文章

订阅专栏

前言

上一篇文章详细解读了论文GoogLeNet网络结构，现在给大家介绍何凯明大神在2016年发表在CVPR的best paper，<Deep Residual Learning for Image Recognition> 开创了深度残差网络的先河，解决了超深层网络训练问题，研究人员不再需要担心随着层数增加而带来的梯度问题，ResNet在2015年ImageNet的图像分类任务中，获得了第一名，并且在top-5错误率上达到了3.57%，大大超过了其他参赛模型。

论文原文：https://arxiv.org/abs/1512.03385

领取100G深度学习资料,500多篇经典论文,论文辅导等请关注作者公众号: 智算学术 回复:资料领取

前景回顾

LeNet 论文精读 | 深度解析+PyTorch代码复现(上)_yann lecun卷积网络的奠定文章-优快云博客

LeNet 论文精读 | 深度解析+PyTorch代码复现(下)_lenet搭建与mnist训练-优快云博客

AlexNet 论文精读 | 深度解析+PyTorch代码复现 (上)-优快云博客

AlexNet 论文精读 | 深度解析+PyTorch代码复现 (下)-优快云博客

VGG论文精读 | 深度解析+PyTorch代码复现_dense convnet evaluation-优快云博客

GoogleNet论文精读 | 深度解析+PyTorch代码复现-优快云博客

三、Deep Residual Learning—深度残差学习

3.1. Residual Learning-残差学习

3.2. Identity Mapping by Shortcuts-通过快捷方式进行身份映射

3.3. Network Architectures-网络架构

3.4. Implementation-实现

四、Experiments--实验

4.1. ImageNet Classification

Identity vs. Projection Shortcuts—恒等 vs 映射 Shortcuts

Deeper Bottleneck Architectures

4.2. CIFAR-10 and Analysis

4.3. Object Detection on PASCAL and MS COCO—PASCAL和MS COCO上的对象检测

Abstract—摘要

翻译

深度神经网络更难训练。我们提出了一种残差学习框架，以简化比以往更深的网络的训练。我们明确地将每一层重新表述为学习相对于层输入的残差函数，而不是学习无参照的函数。我们提供了大量的实验证据，表明这些残差网络更容易优化，并且可以通过显著增加网络深度来提升准确性。在ImageNet数据集上，我们评估了深度达到152层的残差网络——比VGG网络深8倍，但其复杂度仍然较低。一个这些残差网络的集成在ImageNet测试集上取得了3.57%的错误率。这个结果赢得了2015年ILSVRC图像分类任务的第一名。我们还对CIFAR-10数据集上的100层和1000层网络进行了分析。表示的深度对于许多视觉识别任务至关重要。仅仅因为我们具有极深的表示，我们在COCO物体检测数据集上获得了28%的相对提升。深度残差网络是我们提交到ILSVRC和COCO 2015竞赛的基础，在这些竞赛中，我们还赢得了ImageNet检测、ImageNet定位、COCO检测和COCO分割任务的第一名。

精读

为了解决什么问题 深度神经网络在增加层数时面临训练困难，特别是梯度消失和退化问题，导致更深的网络难以有效优化和训练。

做了什么开创性工作 提出了残差学习框架，通过将每一层转换为学习相对于输入的残差函数，而非直接学习映射函数，极大地简化了深层网络的训练过程。该框架允许网络通过“跳跃连接”来传递信息，避免了梯度消失问题。

有什么效果 通过引入残差学习，深度网络的训练变得更加高效。实验结果表明，ResNet能够训练深达152层的网络，取得了3.57%的错误率，在2015年ILSVRC图像分类任务中获得了第一名。此外，残差网络还在COCO数据集上的物体检测任务中提升了28%的相对准确性，并在多个ILSVRC和COCO竞赛任务中赢得了第一名。

如何理解残差函数？

假设你在做一项任务，任务是将一个箱子从一个地方搬到另一个地方。你知道搬家这个任务有很多步骤，比如搬箱子、整理、清理等等。如果你每次都要记住整个搬家的过程，那么你得花费很多时间，记住所有的细节。而如果你只需要记住你在每个步骤中需要做的“改进”或者“变化”，那样是不是会容易一些？这就像**残差网络**的工作方式。传统的神经网络就像是你需要一步步学习整个搬家过程（也就是整个映射），而**残差网络**则不直接去学习整个过程，而是去学习每一步中需要改变或者“改善”的部分（也就是残差）

说的比较形象就是：老大和小弟要去一个陌生的地方，但是呢？每到一个地方，老大不想走路去探路，让小弟去，小弟探好路回来报告给老大，老大直接按照小弟的指路继续前进！

一、Introduction—介绍

翻译

深度卷积神经网络（DCNN）已经为图像分类等任务带来了一系列突破。深度网络自然地将低、中、高层特征与分类器结合成端到端的多层结构，随着层数的增加（网络深度），特征的“层次”得到了丰富。最近的研究表明，网络深度是非常重要的，许多在挑战性数据集ImageNet上的领先结果都使用了“非常深”的模型，深度从16层到30层不等。其他许多复杂的视觉识别任务也从非常深的模型中受益。

随着深度的重要性被逐渐认识，一个问题随之而来：学习更好的网络是否仅仅通过堆叠更多层就能解决？答案并不简单，因为深度网络存在着梯度消失/梯度爆炸的问题，这些问题会从一开始就妨碍网络的收敛。然而，使用归一化初始化和中间归一化层等方法，已经能有效地解决这个问题，使得数十层的网络可以在反向传播算法（SGD）下开始收敛。

当更深的网络开始收敛时，暴露出一个退化问题：随着网络深度的增加，准确率会逐渐饱和（这可能不奇怪），然后迅速下降。令人意外的是，这种退化并不是由过拟合引起的，增加更多层的深度模型反而会导致更高的训练误差。图1显示了一个典型的例子。

训练准确率的退化表明，并非所有的系统都容易优化。假设我们考虑一个较浅的网络架构和它的深层版本，通过添加更多层来扩展它。实际上可以通过构造解决这个问题：添加的层是恒等映射，其余层是从已训练的浅层模型复制过来的。这个构造解的存在表明，较深的网络不应该比浅层网络产生更高的训练误差。但实验结果显示，现有的求解器在找到比构造解更好的解时往往失败，或者在合理的时间内无法完成。因此，本文提出了一种深度残差学习框架来解决退化问题。

在残差网络中，我们不再希望每个堆叠的几层直接拟合一个目标映射，而是让这些层拟合一个残差映射。形式上，设目标映射为 H(x)H(x)H(x)，我们让堆叠的非线性层拟合另一个映射 F(x):=H(x)−xF(x) := H(x) - xF(x):=H(x)−x，即原始映射转化为 F(x)+xF(x) + xF(x)+x。我们假设优化残差映射比直接优化原始的未参考映射更容易。极端情况下，如果恒等映射是最优的，那么将残差推向零比通过一堆非线性层拟合恒等映射要容易。

这种 F(x)+xF(x) + xF(x)+x 的形式可以通过带有快捷连接（shortcut connections）的前馈神经网络来实现。快捷连接是指跳过一层或多层，在我们的网络中，快捷连接执行的是恒等映射，并将其输出加到堆叠层的输出上。恒等快捷连接不会增加额外的参数或计算复杂度。整个网络仍然可以通过反向传播算法使用SGD进行端到端的训练，并且可以使用常见的深度学习库（如Caffe）轻松实现，而无需修改求解器。

我们在ImageNet数据集上进行了全面的实验，展示了退化问题，并评估了我们的方法。实验结果表明：

我们的极深残差网络更容易优化，而相应的“普通”网络（直接堆叠层）随着深度增加，训练误差更高；
我们的深度残差网络可以从大幅增加的深度中获益，准确率大幅提升，超越了以前的网络。

在CIFAR-10数据集上也观察到了类似的现象，表明我们的优化方法和效果不仅仅适用于特定的数据集。我们成功训练了超过100层的模型，并探索了超过1000层的模型。在ImageNet分类数据集上，我们的152层残差网络是目前在该数据集上提出的最深网络，且其复杂度低于VGG网络。我们的集成模型在ImageNet测试集上的Top-5错误率为3.57%，并赢得了2015年ILSVRC图像分类比赛的第一名。极深的表示还在其他识别任务中表现优异，帮助我们在ILSVRC和COCO 2015竞赛中获得了ImageNet检测、ImageNet定位、COCO检测和COCO分割任务的第一名。

这些强有力的证据表明，残差学习原理具有普适性，我们预计它不仅适用于视觉问题，也适用于其他非视觉问题。

精读

1. 传统的神经网络遇到了什么问题

传统的深度神经网络面临以下几个问题：

梯度消失/爆炸问题：随着网络层数的增加，梯度在反向传播时容易消失或爆炸，这会导致训练过程中的收敛困难，特别是在深层网络中。
退化问题：尽管网络深度的增加理论上应该提高网络的表达能力，但实际上，随着网络深度的增加，训练准确率反而会先饱和然后迅速下降。这并不是由于过拟合引起的，而是由于深度增加后，优化变得更加困难，导致模型无法有效训练。
训练误差增加：在网络层数增加时，传统神经网络的训练误差并没有减少，反而有所增加，说明现有的优化方法难以有效处理深层网络。

2. 怎么解决的

为了应对上述问题，本文提出了残差学习框架，通过以下方式解决：

残差学习：通过将每层的目标从学习原始映射转换为学习“残差”映射，网络不再直接拟合目标映射，而是拟合输入与目标之间的差异（残差）。这种方法简化了优化过程，使得训练更加容易。
恒等映射（Shortcut Connections）：残差网络使用快捷连接（shortcut connections），这些连接将输入直接加到输出上，避免了传统网络中每一层都必须学习复杂映射的问题。恒等快捷连接不会增加额外的参数或计算复杂度，从而使得网络可以更深而不至于出现退化问题。
深度残差网络：通过这些设计，网络的深度得以大幅增加，且能保持或提高训练准确度。实验结果表明，深度残差网络不仅解决了退化问题，而且比传统网络能在更大深度下获得更好的性能。

二、Related Work—相关工作

翻译

残差表示：在图像识别中，VLAD（Vector of Locally Aggregated Descriptors）[18]是一种通过与字典的残差向量编码的表示方法，而Fisher向量[30]可以被表述为VLAD的概率版本[18]。它们都是强大的浅层表示，用于图像检索和分类[4, 48]。对于向量量化，编码残差向量[17]被证明比编码原始向量更有效。在低层次视觉和计算机图形学中，为了解决偏微分方程（PDE），广泛使用的多重网格方法[3]将系统重新构造为多个尺度下的子问题，每个子问题负责处理粗尺度和细尺度之间的残差解。多重网格的替代方法是分层基预处理[45, 46]，它依赖于表示两个尺度之间残差向量的变量。已有研究表明[3, 45, 46]，这些求解器的收敛速度远快于标准求解器，后者未能考虑到解的残差特性。这些方法表明，良好的重构或预处理可以简化优化过程。

快捷链接：早期的实践和理论研究表明，快捷连接[2, 34, 49]已经被研究了很长时间。多层感知机（MLP）训练的一个早期实践是增加一个从网络输入到输出的线性层连接[34, 49]。在[44, 24]中，一些中间层直接连接到辅助分类器，以解决梯度消失/爆炸问题。[39, 38, 31, 47]的论文提出了通过快捷连接来对层响应、梯度和传播误差进行中心化的方法。在[44]中，一个“inception”层由一个快捷分支和几个更深的分支组成。与我们工作同时进行的“highway networks”[42, 43]提出了带有门控函数[15]的快捷连接。与我们使用的恒等快捷连接不同，这些门控是数据依赖的并且有参数。当门控快捷连接“关闭”时（接近零），highway网络中的层表示非残差函数。与此相反，我们的公式始终学习残差函数；我们的恒等快捷连接从不关闭，所有信息始终被传递，并且额外的残差函数会被学习。此外，highway网络在极深层次（例如，超过100层）时并未表现出准确度的提升。

精读

残差表示：（大白话式理解）在处理图像时，使用“残差”来表示数据比直接使用原始数据更有效。就像做数学题时，把一个复杂问题拆成多个小问题来解决，速度更快。类似地，一些图像处理方法也通过拆解问题，提高了效率。

快捷连接：（大白话式理解）快捷连接就是直接把输入信息跳过某些层，直接传递到后面的层。这就像是有人给你传递消息时，直接绕过中间的复杂步骤，节省时间。我们的方法是一直让信息传递，不关闭这些跳过的连接，而有些其他方法（如highway网络）则会根据情况来关闭这些连接。但对于非常深的网络（比如超过100层），其他方法没能提高准确率，而我们的做法在这种情况下效果更好。

三、Deep Residual Learning—深度残差学习

3.1. Residual Learning-残差学习

翻译

我们考虑将 H(x)作为一个需要通过几层堆叠的层来拟合的基础映射（不一定是整个网络），其中 x是这些层的输入。如果假设多个非线性层能够渐近地逼近复杂的函数，那么它也等价于假设它们能够渐近地逼近残差函数，即 H(x)−x（假设输入和输出的维度相同）。因此，与其期望堆叠的层直接拟合 H(x)，我们显式地让这些层拟合一个残差函数 F(x):=H(x)−x。原始的函数因此变成了 F(x)+x。尽管这两种形式在渐近上应该都能逼近所期望的函数（如假设所述），但学习的难易程度可能不同。这种重构的动机来自于有关退化问题的反直觉现象（图1左）。正如我们在引言中讨论的，如果新增的层可以构建为恒等映射，则更深的模型应该具有不大于其浅层对比模型的训练误差。退化问题表明，求解器可能在通过多个非线性层来逼近恒等映射时遇到困难。通过残差学习的重构，如果恒等映射是最优的，求解器可以简单地将多个非线性层的权重驱动到零，以接近恒等映射。在实际情况下，恒等映射不太可能是最优的，但我们的重构可能有助于对问题进行预处理。如果最优函数更接近恒等映射而非零映射，那么求解器应该更容易找到以恒等映射为参考的扰动，而不是将函数学习为一个全新的函数。通过实验（图7），我们表明学习到的残差函数通常响应较小，这表明恒等映射为预处理提供了合理的基础。

精读

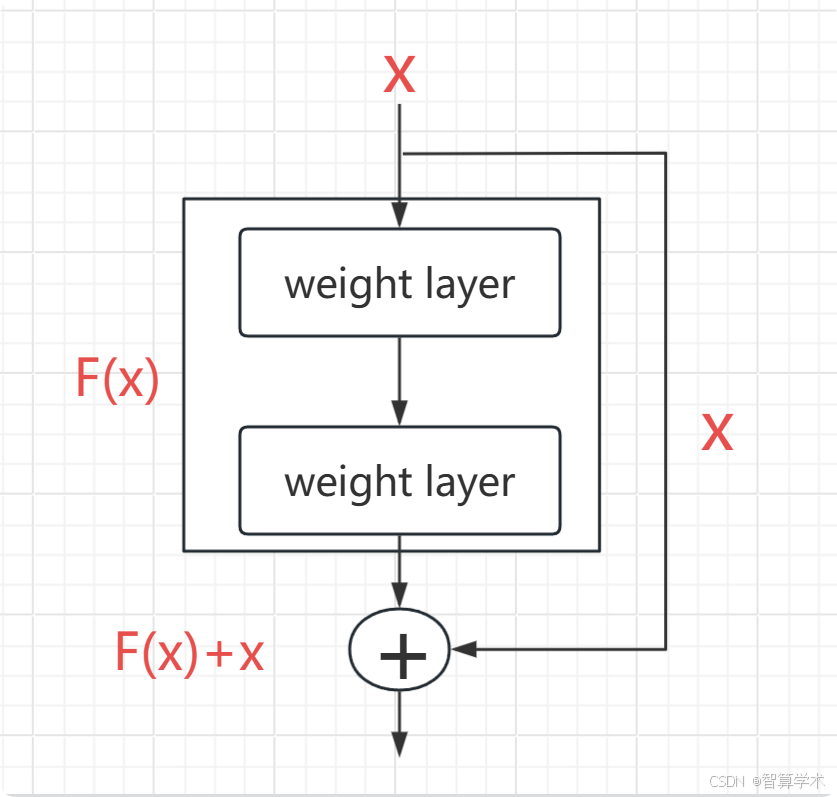
如何理解残差函数？

X 是输入特征矩阵也就是原始矩阵，在传统的神经网络结构中，直接F(x)+x 进行训练，但是在残差网络中，我另外接了一根线，也就是说原始矩阵x，它有了选择权，当F（x）训练的参数是垃圾参数或者说是对我们最终的结果起反作用时，原始矩阵x可以选择跳过F(x)，这样的话就能保证最起码特征矩阵带的信息不会因为F(x)的垃圾参数的原因丢失信息，也就是说经过变换的特征矩阵接近于恒等于最原始的矩阵，保证了不会因为超深的神经网络因为太深的结构而导致信息丢失

3.2. Identity Mapping by Shortcuts-通过快捷方式进行身份映射

翻译

我们在每几个堆叠的层上采用残差学习。一个基本的残差块如图 2 所示。形式上，在本文中，我们将基本残差块定义为：y = F(x, {Wi}) + x，其中，x 和 y 分别是所考虑层的输入和输出向量。函数 F(x, {Wi}) 代表需要学习的残差映射。例如，在图 2 所示的两层结构中，残差映射为：F = W2σ(W1x)，其中，σ 表示 ReLU 激活函数 [29]，为了简化符号省略了偏置项。运算 F + x 通过一个快捷连接（shortcut connection）和逐元素加法（element-wise addition）来实现。我们在加法后应用第二个非线性变换（即 σ(y)，见图 2）。在公式 (1) 中的快捷连接不会引入额外的参数或计算复杂度。这不仅在实际应用中很有吸引力，而且在对比普通网络和残差网络时尤为重要。这样，我们可以在相同的参数量、深度、宽度和计算成本（除了可以忽略的逐元素加法）下，公平地比较普通网络和残差网络。

在公式 (1) 中，x 和 F 的维度必须相等。如果不相等（例如在改变输入/输出通道数时），我们可以通过快捷连接使用线性投影 Ws 来匹配维度：y = F(x, {Wi}) + Ws x，在公式 (1) 中，我们也可以使用方阵 Ws。但我们通过实验表明，恒等映射（identity mapping）已经足够解决退化问题，并且更具计算经济性，因此 Ws 仅用于匹配维度。

残差函数 F 的形式是灵活的。在本文的实验中，F 包含两层或三层（见图 5），但也可以使用更多层。然而，如果 F 只有一层，公式 (1) 变为：y = W1 x + x，在这种情况下，我们并未观察到性能上的优势。此外，尽管上述符号是针对全连接层的，但同样适用于卷积层。函数 F(x, {Wi}) 可以表示多个卷积层，并且逐元素加法是在两个特征图上按通道进行的。

精读

残差块是怎么设计的？

一个 残差块（Residual Block） 就是多个神经网络层的组合，并且有一个「快捷连接（Shortcut Connection）」直接把输入 x 传递到输出 y，公式如下：y = F(x, {Wi}) + x

其中：

F(x, {Wi}) 代表要学习的残差映射，通常由几层神经网络组成（比如 W2σ(W1x)，即两层带 ReLU 的全连接层）。
F + x 通过「快捷连接」进行逐元素加法（element-wise addition）。
计算完 y 之后，还会再加一个非线性激活函数（比如 ReLU）

如果输入和输出的维度不匹配怎么办？ 可以用一个 线性投影（Ws） 来调整维度，比如：y = F(x, {Wi}) + Ws X ,就是调整一下 x 的输入维度，来和F（x）的尺寸适配后，好做加和计算

3.3. Network Architectures-网络架构

翻译

我们测试了多种普通网络（plain nets）和残差网络（residual nets），并观察到了一些一致的现象。为了便于讨论，我们描述了两个在 ImageNet 上的模型如下。

普通网络：我们的普通网络基线（图 3 中间）主要受到 VGG 网络 [41]（图 3 左侧）设计理念的启发。卷积层主要采用 3×3 的卷积核，并遵循以下两个简单的设计规则：

对于相同的输出特征图尺寸，使用相同数量的滤波器（filters）。
当特征图尺寸减半时，滤波器数量加倍，以保持每层的计算复杂度不变。

为了进行下采样（downsampling），我们直接使用步长（stride）为 2 的卷积层。网络的最后一层是全局平均池化层（Global Average Pooling），接着是一个 1000 维全连接层（Fully Connected Layer）和 Softmax 层。

该网络的总权重层数为 34 层（见图 3 中间）。值得注意的是，相比 VGG 网络（图 3 左），我们的模型使用更少的滤波器，计算复杂度更低。我们的 34 层普通网络计算量为 3.6G FLOPs（乘加运算次数），仅为 VGG-19（19.6G FLOPs）的 18%。

残差网络：基于上述普通网络，我们加入了快捷连接（Shortcut Connections）（见图 3 右侧），将其转换为残差网络。

当输入和输出维度相同时（图 3 中的实线快捷连接），我们可以直接使用恒等映射（Identity Mapping），即公式（1）：y = F(x, {Wi}) + x，当维度发生变化时（图 3 中的虚线快捷连接），我们考虑以下两种方案：

方案 A：仍然使用恒等映射，但用额外的零填充（zero-padding）来匹配更高的维度。这种方法不会引入额外的参数。
方案 B：使用公式（2）中的投影映射（Projection Shortcut），通过 1×1 卷积来匹配维度：y = F(x, {Wi}) + Ws x，对于以上两种方案，当快捷连接跨越不同尺寸的特征图时，我们采用步长（stride）= 2 进行计算。

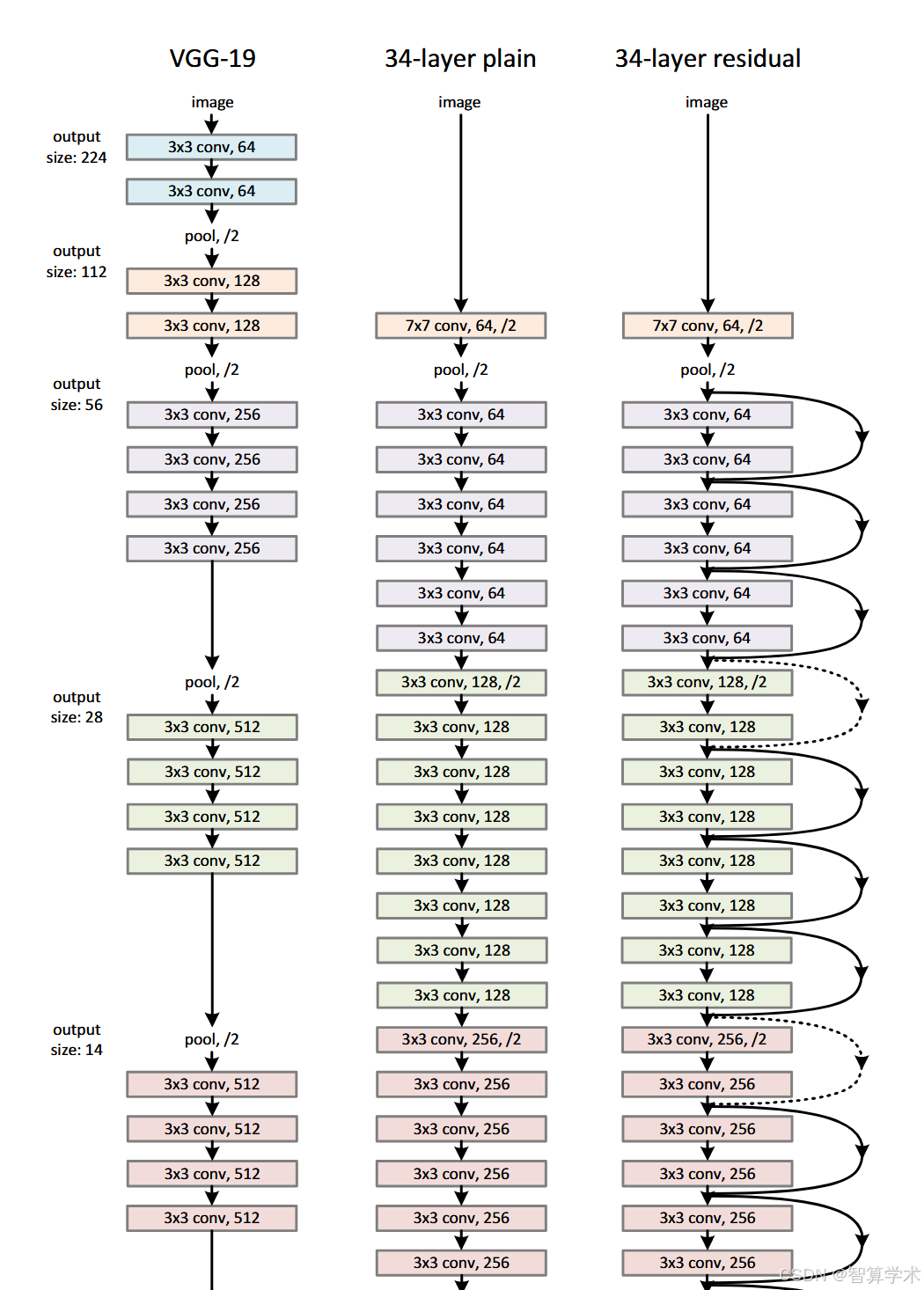
精读

普通网络（Plain Network）
- 这个网络的设计灵感来源于VGG网络，采用的卷积核大多数是3x3的，设计上有两个简单的规则：
  1. 如果输出的特征图尺寸相同，网络的每一层卷积的滤波器（卷积核）的数量也相同。
  2. 如果特征图的尺寸减半，那卷积的滤波器数量就会翻倍，保持每一层计算量差不多。
- 通过卷积层进行下采样（图像尺寸缩小），最后加一个全局平均池化层和一个1000类的全连接层进行分类。
- 和VGG网络相比，这个普通网络的滤波器数量更少，复杂度更低。
残差网络（Residual Network）
- 在普通网络的基础上，增加了shortcut连接，形成了残差网络。
- 输入和输出维度相同时，可以直接使用恒等映射（就是直接把输入加到输出上，不做其他改动），这种连接方式没有增加额外的参数。
- 当维度增加时，有两种处理方式：
  - 方式A：依然使用恒等映射，只是通过填充零来调整维度，避免了新增参数。
  - 方式B：使用投影shortcut，利用1x1的卷积来调整维度。
- 对于不同尺寸的特征图，shortcut连接会以步幅2来进行处理。

总结： ResNet的核心思想就是通过shortcut连接（也叫残差连接）来解决深层网络训练时的“退化问题”。也就是说，深层网络的表现可能因为层数过多而变得不如浅层网络，但残差连接可以让每一层网络学习到一个“残差”，而不是直接去学习一个完整的输出。这样，网络不仅能加深，而且还能保持或者提高性能，同时减少计算复杂度。

3.4. Implementation-实现

翻译

我们的ImageNet实现遵循了[21, 41]中的做法。图像会根据较短边随机调整尺寸，范围在[256, 480]之间，以进行尺度增强[41]。然后从图像中随机裁剪出224×224的区域，或者进行水平翻转，并减去每个像素的均值[21]。我们使用了[21]中的标准颜色增强方法。在每个卷积层后和激活函数前，我们都采用批量归一化（BN）[16]。我们按[13]中的方法初始化权重，并从头开始训练所有的plain/residual网络。我们使用小批量大小为256的SGD。学习率从0.1开始，当误差停滞时，学习率除以10，模型训练最多进行60 × 10^4次迭代。我们使用0.0001的权重衰减和0.9的动量。我们不使用dropout[14]，遵循[16]中的做法。在测试时，为了进行比较研究，我们采用标准的10裁剪测试[21]。为了获得最佳结果，我们采用了[41, 13]中的全卷积形式，并在多个尺度下平均得分（图像的短边调整为{224, 256, 384, 480, 640}中的某个值）。

精读

数据增强：
- 图像的短边会被随机调整大小，范围在256到480之间，用于尺度增强。
- 从调整后的图像中随机裁剪出224×224的区域，或者进行水平翻转。
- 在每个像素上减去其均值，以进行标准化处理。
批量归一化（Batch Normalization）：
- 在每个卷积层后面加上批量归一化，归一化操作在激活函数前进行，以加速训练和提高稳定性。
权重初始化：
- 所有的权重初始化方法遵循特定的规则（参考文献中提到的方法）。
训练策略：
- 使用SGD（随机梯度下降）优化器，批量大小为256。
- 初始学习率为0.1，当误差不再下降时，学习率会降低10倍。
- 模型训练总共进行60万次迭代。
- 使用权重衰减（0.0001）和动量（0.9）来防止过拟合。
未使用Dropout：
- 根据参考文献中的方法，没有使用dropout。
测试时的标准方法：
- 使用标准的10裁剪方法进行测试，确保多个裁剪结果能够反映模型的准确性。
多尺度测试：
- 为了获得最佳结果，采用了多尺度方法：将图像调整为不同尺寸（224、256、384、480、640），并对多个尺度的结果进行平均。

总结来说，模型训练通过数据增强、批量归一化、权重初始化、适当的优化策略、以及多尺度测试等手段来确保更好的训练效果和预测性能。

四、Experiments--实验

4.1. ImageNet Classification

翻译

我们在ImageNet 2012分类数据集[36]上评估了我们的方法，该数据集包含1000个类别。模型在128万张训练图像上进行训练，在5万张验证图像上进行评估。最终结果是在10万张测试图像上得出的，由测试服务器报告。我们评估了top-1和top-5错误率。

Plain网络 我们首先评估了18层和34层的plain网络。34层的plain网络如图3（中）所示，18层的plain网络与其结构类似。具体架构详见表1。表2的结果显示，深层的34层plain网络的验证错误率高于较浅的18层plain网络。为了揭示原因，在图4（左）中，我们比较了它们在训练过程中的训练/验证误差。我们观察到了退化问题——即使18层plain网络的解空间是34层plain网络的子空间，34层plain网络在整个训练过程中训练误差始终较高。我们认为，这种优化困难不太可能是由于梯度消失导致的。这些plain网络是使用BN[16]训练的，BN确保了前向传播的信号具有非零方差。我们还验证了反向传播的梯度也有健康的范数，说明前向和反向信号都没有消失。事实上，34层plain网络仍然能够达到具有竞争力的准确率（表3），表明求解器在某种程度上是有效的。我们推测，深层plain网络可能有非常低的收敛速度，这影响了训练误差的减少。我们将在未来研究这种优化困难的原因。

Residual网络 接下来，我们评估了18层和34层的Residual网络（ResNet）。基础架构与上述plain网络相同，只是在每对3×3卷积层中添加了shortcut连接，如图3（右）所示。在第一次比较中（表2和图4右），我们对所有shortcut使用了身份映射，并对维度增加进行了零填充（选项A）。因此，它们与plain网络相比没有额外的参数。

从表2和图4中我们得出三个主要观察结果。首先，使用残差学习的情况有所逆转——34层ResNet比18层ResNet表现更好（提高了2.8%）。更重要的是，34层ResNet展示了显著较低的训练误差，并且能够更好地推广到验证数据。这表明，退化问题在这种设置下得到了有效解决，我们通过增加深度获得了准确度的提升。其次，与plain网络相比，34层ResNet将top-1错误率减少了3.5%（表2），这得益于训练误差的成功减少（图4右 vs. 左）。这个比较验证了残差学习在极深网络中的有效性。最后，我们还注意到，18层的plain/residual网络在准确性上相当接近（表2），但18层ResNet收敛速度更快（图4右 vs. 左）。当网络不是“过深”时（此处是18层），当前的SGD求解器仍然能够为plain网络找到好的解。在这种情况下，ResNet通过提供更快的收敛速度，在训练的早期阶段缓解了优化问题。

精读

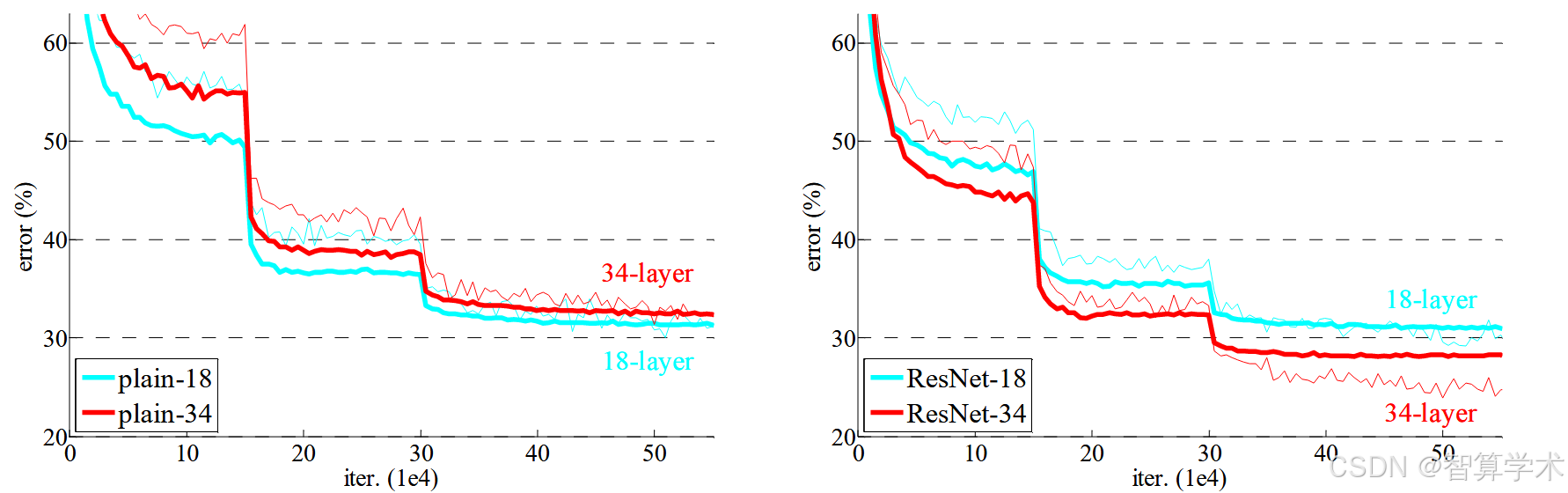
讨论了在ImageNet数据集上评估不同深度的Plain网络和Residual网络（ResNet）表现的实验结果。

Plain网络：
- 研究了18层和34层的plain网络。34层网络比18层网络深，但是发现34层网络的训练误差比18层高，表现不如18层。虽然两者的解空间有重叠，但34层网络仍然难以训练，可能是因为它们收敛得非常慢，导致训练误差难以下降。
- 由于使用了Batch Normalization（BN），前向和反向的信号没有消失，梯度也正常。这个训练困难可能并非由于梯度消失，而是因为深度增加导致网络优化变得更加困难。
Residual网络（ResNet）：
- 引入shortcut连接（残差连接）后，34层的ResNet比18层的ResNet表现更好，训练误差显著降低，模型也能更好地推广到验证数据集。
- 使用残差学习后，34层的ResNet比18层ResNet减少了更多的错误（top-1误差减少了3.5%）。这表明，使用残差学习的网络可以有效解决深层网络的退化问题，且通过增加深度能够提升性能。
- 当网络深度相对较浅（18层）时，ResNet能够更快地收敛，比plain网络更有效。

总结：Residual网络（ResNet）通过引入shortcut连接，解决了深层网络的退化问题，使得更深的网络能够有效训练，并且在测试中取得了更好的结果。

Identity vs. Projection Shortcuts—恒等 vs 映射 Shortcuts

翻译

我们已经展示了无参数的恒等快捷连接有助于训练。接下来，我们研究了投影快捷连接（公式(2)）。在表3中，我们比较了三种选项：（A）对于增加维度的情况，使用零填充快捷连接，所有快捷连接都是无参数的（与表2和图4右侧相同）；（B）对于增加维度的情况，使用投影快捷连接，其他快捷连接为恒等连接；（C）所有的快捷连接都是投影连接。表3显示，这三种选项都比普通的网络有显著的提升，选项B稍微优于选项A。我们认为这是因为在选项A中，零填充的维度没有残差学习。选项C稍微优于选项B，我们认为这是由于引入了多个（十三个）投影快捷连接，增加了额外的参数。但选项A/B/C之间的小差异表明，投影快捷连接对于解决退化问题并非必须。因此，在本文其余部分我们不使用选项C，以减少内存/时间复杂度和模型大小。恒等快捷连接在不增加瓶颈架构复杂度方面尤其重要，下面将介绍这种架构。

精读

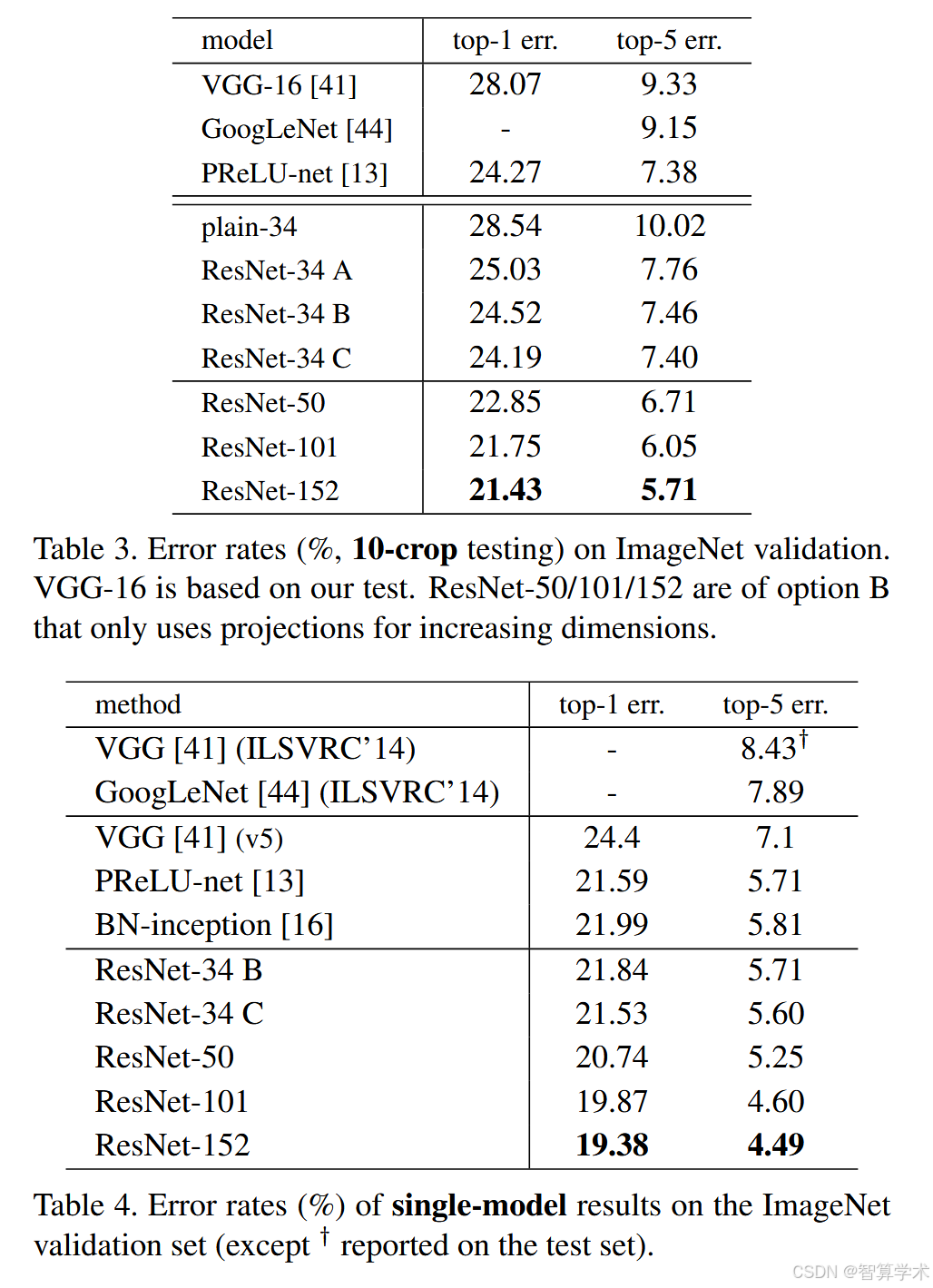
在这部分，作者比较了三种不同类型的快捷连接（shortcut connections）：

零填充快捷连接（选项A）：当网络维度增加时，使用零填充来补充新的维度，这样没有额外的学习参数。
投影快捷连接（选项B）：对于增加维度的部分，使用投影（即使用1×1卷积）来调整维度，其他地方仍然使用恒等连接。
全部投影快捷连接（选项C）：所有的维度都通过卷积核（即使用1×1卷积）来进行调整。

实验结果表明，三种选项都比普通网络（没有任何快捷连接）要好。具体来说，选项B（部分投影快捷连接）比选项A（零填充快捷连接）稍微好一点，因为零填充并没有实现任何实际的残差学习。而选项C（全部投影快捷连接）略微优于选项B，但差别不大，主要是因为选项C引入了更多的参数，导致模型变得更加复杂。

通过这些比较，作者得出结论：虽然投影快捷连接能进一步提升性能，但对于解决“退化问题”来说并非必须。因此，在后续的研究中，作者选择不使用选项C，以减少模型的复杂度（如内存和计算量），并保持恒等快捷连接的优势，尤其是在处理一些复杂网络结构时，恒等快捷连接有助于避免增加计算复杂度。

Deeper Bottleneck Architectures

翻译

接下来，我们描述了针对ImageNet的更深网络。考虑到训练时间的限制，我们将构建块修改为瓶颈设计。对于每个残差函数F，我们使用一个由三层堆叠组成的结构，而不是两层（见图5）。这三层分别是1×1、3×3和1×1的卷积，其中1×1层负责减少和恢复维度，而3×3层则作为瓶颈，具有较小的输入/输出维度。图5展示了一个例子，其中两种设计具有相似的时间复杂度。参数无关的身份快捷方式对瓶颈架构尤其重要。如果将图5（右）中的身份快捷方式替换为投影，时间复杂度和模型大小将翻倍，因为快捷方式连接到两个高维的端点。因此，身份快捷方式使得瓶颈设计的模型更加高效。

50层ResNet：我们将34层网络中的每个2层块替换为这个3层的瓶颈块，从而得到了50层的ResNet（见表1）。我们使用选项B来增加维度。该模型有38亿FLOP。

101层和152层ResNet：通过使用更多的3层块，我们构建了101层和152层的ResNet（见表1）。值得注意的是，尽管深度大幅增加，但152层的ResNet（113亿FLOP）仍然比VGG-16/19网络（分别为153亿/196亿FLOP）的复杂度低。50/101/152层的ResNet在准确性上都显著优于34层网络（见表3和表4）。我们没有观察到退化问题，因此从大幅增加的深度中获得了显著的准确性提升。在所有评估指标中，深度的优势都得到了体现（见表3和表4）。

与最先进方法的比较：在表4中，我们与之前最佳的单模型结果进行了比较。我们的34层ResNet基线模型已经达到了非常有竞争力的准确性。我们的152层ResNet在验证集上的单模型top-5错误率为4.49%。这个单模型结果超越了所有之前的集成结果（见表5）。我们将六个不同深度的模型进行集成（提交时只包含两个152层的模型）。这使得测试集上的top-5错误率达到了3.57%（见表5）。该成绩在2015年ILSVRC中获得了第一名。

精读

瓶颈设计：为了优化训练时间，采用了瓶颈设计，即每个残差模块由三层卷积层组成：1×1、3×3、1×1。1×1卷积层负责减小和恢复维度，3×3卷积层则是瓶颈，减少输入和输出的维度，提升计算效率。

网络深度增加：通过将34层ResNet的2层模块替换为3层瓶颈设计，得到了50层ResNet。更深的网络包括101层和152层ResNet，尽管深度增加，152层的ResNet仍比VGG-16和VGG-19的复杂度低。

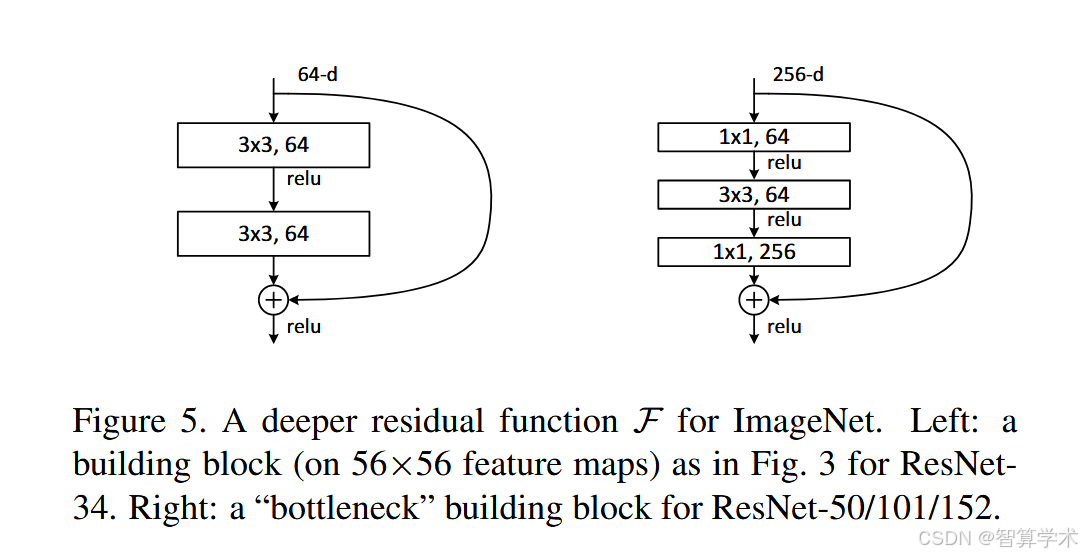
减少计算负担：瓶颈设计有效地减少了计算复杂度，使得深度更大的网络在计算上更高效。

提升准确率：50层、101层和152层ResNet相较于34层网络，在准确性上有显著提升，且没有出现退化问题。

152层ResNet表现：152层ResNet在验证集上的top-5错误率为4.49%，超过了所有以前的集成模型。

集成模型：他们将六个不同深度的ResNet模型组合成一个集成模型，达到了3.57%的top-5错误率，获得了2015年ILSVRC比赛的第一名。

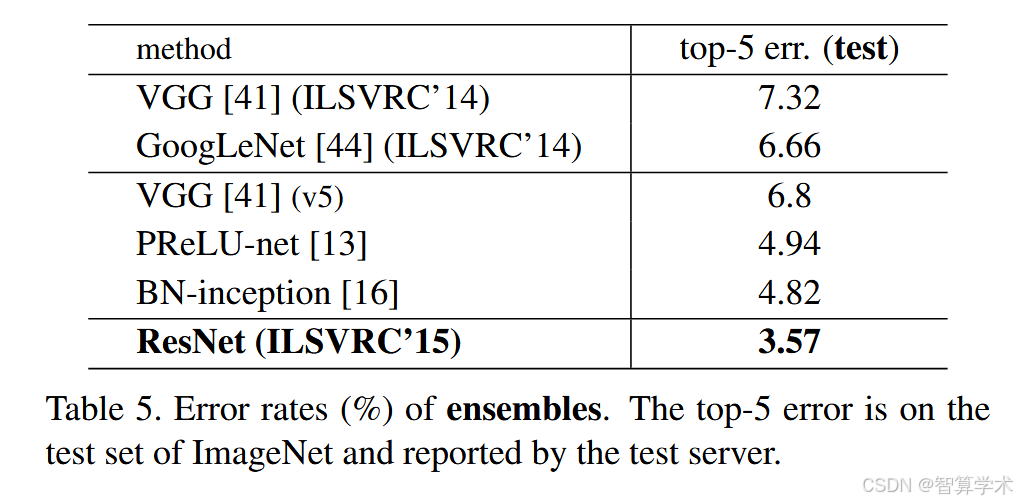
结论：通过优化深度和瓶颈设计，成功解决了深度增加带来的训练问题，显著提升了模型的准确性，并在图像分类任务中获得了优秀的成绩。

4.2. CIFAR-10 and Analysis

翻译

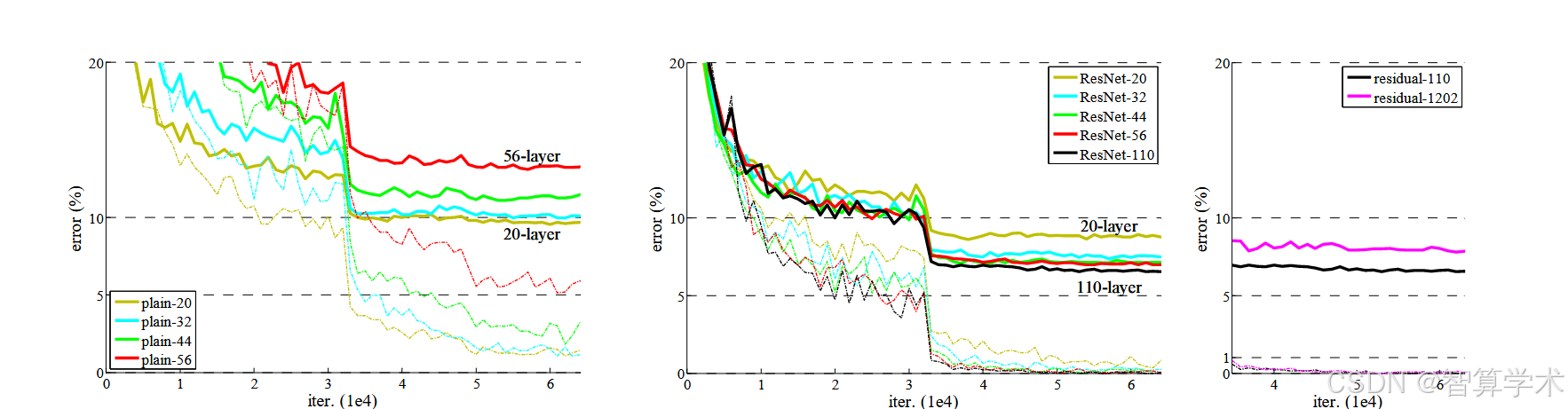
我们在 CIFAR-10 数据集上进行了更多的研究。CIFAR-10 数据集包含 50,000 张训练图像和 10,000 张测试图像，共有 10 个类别。我们展示了在训练集上训练并在测试集上评估的实验。我们关注的是极深网络的表现，而不是追求最先进的结果，因此我们故意使用简单的架构，具体如下：平凡/残差架构遵循图 3（中/右）的形式。网络输入是 32×32 的图像，且每个像素减去均值。第一层是 3×3 的卷积层。然后，我们使用一系列 6n 层的堆叠结构，分别在特征图大小为 {32, 16, 8} 上进行 3×3 卷积，每个特征图大小有 2n 层。滤波器的数量分别是 {16, 32, 64}。下采样通过步幅为 2 的卷积进行。网络以全局平均池化、一个 10 类的全连接层和 Softmax 层结束。总共有 6n+2 层加权层。下表总结了架构：当使用快捷连接时，它们连接到每对 3×3 层（总共 3n 个快捷连接）。在这个数据集上，我们在所有情况下使用身份快捷连接（即选项 A），因此我们的残差模型在深度、宽度和参数数量上与平凡网络完全相同。我们使用 0.0001 的权重衰减和 0.9 的动量，并采用 [13] 中的权重初始化和 BN [16]，但不使用 dropout。我们在两块 GPU 上以小批量大小 128 进行训练。我们从 0.1 的学习率开始，在 32k 和 48k 次迭代时将其除以 10，并在 64k 次迭代时终止训练，训练是基于 45k/5k 的训练/验证划分进行的。我们遵循 [24] 中的简单数据增强方法进行训练：在每一边填充 4 个像素，并从填充后的图像中随机采样一个 32×32 的裁剪或其水平翻转。测试时，我们只评估原始 32×32 图像的单视角。我们比较了 n = {3, 5, 7, 9}，得到 20、32、44 和 56 层的网络。图 6（左）展示了平凡网络的表现。深层平凡网络在深度增加时表现出更高的训练误差。这一现象与 ImageNet（图 4 左）和 MNIST（见 [42]）上的表现相似，表明这种优化难题是一个基本问题。图 6（中）展示了 ResNets 的表现。与 ImageNet 的情况相似（图 4 右），我们的 ResNets 成功克服了优化难题，并且随着深度的增加，表现得到了提升。我们进一步探讨了 n = 18，得到了 110 层的 ResNet。在这种情况下，我们发现 0.1 的初始学习率稍大，不适合开始收敛，因此我们使用 0.01 进行训练热身，直到训练误差低于 80%（大约 400 次迭代），然后再恢复到 0.1 并继续训练。其余的学习调度与之前相同。这个 110 层的网络收敛得很好（图 6 中）。它的参数比其他深而薄的网络（如 FitNet [35] 和 Highway [42]）少（见表 6），但仍处于最先进的结果（6.43%，表 6）。

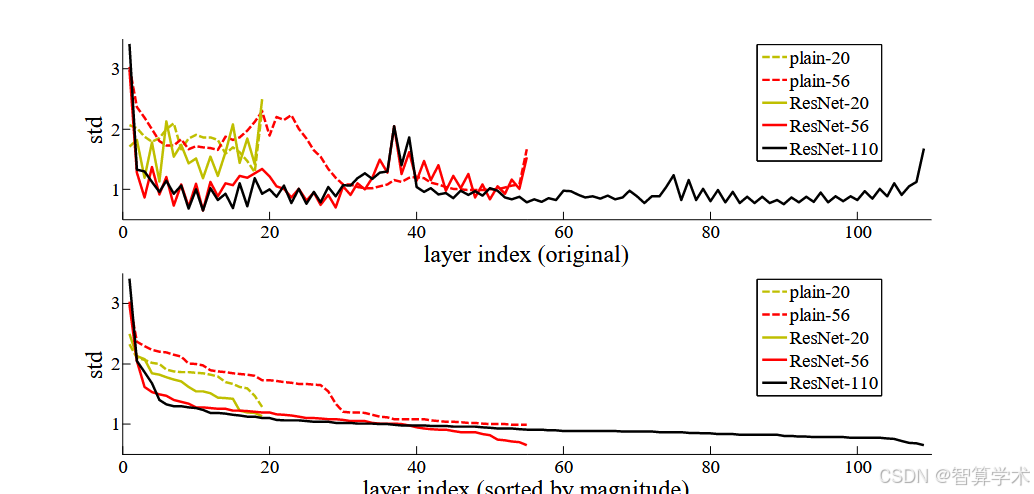
层响应分析：图 7 展示了各层响应的标准差（std）。这些响应是每个 3×3 层的输出，经过 BN 和其他非线性函数（ReLU/addition）之前的结果。对于 ResNets，这一分析揭示了残差函数的响应强度。图 7 显示，ResNets 的响应通常比其平凡网络的响应小。这些结果支持了我们基本动机（见第 3.1 节）的观点，即残差函数通常比非残差函数更接近零。我们还注意到，随着 ResNet 网络深度的增加，响应的幅度逐渐减小，从 ResNet-20、56 和 110 的比较中可以看出。层数越多，ResNet 中的每一层对信号的修改越小。

探索 1000 层以上的网络：我们探索了一个超过 1000 层的极深网络。我们设置 n = 200，得到一个 1202 层的网络，按照上述方式进行训练。我们的模型没有遇到优化困难，这个 1202 层的网络能够实现训练误差 <0.1%（图 6 右）。其测试误差仍然较好（7.93%，见表 6）。但是，这种极深模型仍然存在一些未解问题。这个 1202 层的网络的测试结果不如我们的 110 层网络，尽管它们的训练误差相似。我们认为这是因为过拟合。对于这个小数据集，1202 层的网络可能过于庞大（19.4M 参数）。强正则化（如 maxout [10] 或 dropout [14]）可以用于获得该数据集上的最佳结果（见 [10, 25, 24, 35]）。在本文中，我们没有使用 maxout/dropout，而是通过深而薄的架构设计对模型进行了正则化，以便不偏离优化难题的研究重点。但是，结合更强的正则化可能会改善结果，这一点我们将在未来的研究中进一步探讨。

精读

实验设置：

数据集：使用 CIFAR-10 数据集，包含 50,000 张训练图像和 10,000 张测试图像，分为 10 个类别。
网络架构：实验主要关注非常深的网络，但不追求最先进的结果。使用了简单的架构，其中包括平凡（plain）和残差（residual）架构，输入是 32×32 的图像，经过预处理（像素均值减去）。网络结构采用 3×3 的卷积层，并堆叠 6n 层卷积层，层数随 n 的不同而变化。

模型设计：

网络结构中每层卷积的滤波器数量为 {16, 32, 64}，特征图尺寸分别为 {32, 16, 8}。
下采样通过步幅为 2 的卷积实现，网络最后使用全局平均池化，接一个 10 类的全连接层并通过 Softmax 进行分类。
在使用残差连接时，所有的快捷连接都是身份连接（即选项 A）。

训练设置：

使用权重衰减（0.0001）和动量（0.9），采用 BN（批归一化）进行训练，但不使用 dropout。
采用 mini-batch 训练，批量大小为 128，使用两块 GPU。
学习率初始值为 0.1，每训练 32k 和 48k 次迭代后学习率分别除以 10，训练在 64k 次迭代时结束。
数据增强方法：每边填充 4 像素，随机裁剪或水平翻转图像。

深度网络表现：

平凡网络：随着深度增加，训练误差升高，表现出优化难题。这个问题在 CIFAR-10、ImageNet 和 MNIST 数据集上都存在，表明这是一个基本的优化难题。
残差网络（ResNet）：相比平凡网络，ResNet 成功克服了优化难题，并且随着网络深度的增加，准确率提高。

110 层网络实验：

在 n = 18 时，得到了一个 110 层的 ResNet。在初始学习率为 0.1 时，网络收敛较慢，因此使用了更小的学习率 0.01 来热身训练，直到训练误差低于 80%，然后恢复为 0.1 继续训练。这个 110 层网络收敛良好，且参数量比其他深而薄的网络（如 FitNet 和 Highway）少，但表现接近最先进的结果。

层响应分析：

通过分析每层的标准差（响应的幅度），发现 ResNet 网络的每一层响应普遍小于平凡网络。这表明，残差函数可能更接近零，且随着网络层数增加，单个层对信号的修改逐渐减小。

探索 1000 层以上的网络：

实验中还探索了一个超过 1000 层的网络。通过设置 n = 200，构建了一个 1202 层的网络，成功避免了优化困难，并且训练误差小于 0.1%。但是，这个网络的测试误差（7.93%）高于 110 层的网络，可能是因为过拟合问题。网络参数过多（19.4M）导致在小数据集上表现不如预期。

过拟合和正则化：

对于深度超过 1000 层的网络，可能会出现过拟合，因为网络参数过多，而 CIFAR-10 数据集比较小。为了避免过拟合，通常会使用更强的正则化方法，如 maxout 或 dropout，尽管本文没有使用这些方法，而是通过设计深而薄的架构进行正则化。未来研究可能会探索结合强正则化方法来进一步提高结果。

4.3. Object Detection on PASCAL and MS COCO—PASCAL和MS COCO上的对象检测

翻译

我们的方法在其他识别任务上也表现出良好的泛化性能。表7和表8展示了在PASCAL VOC 2007和2012 [5]以及COCO [26]数据集上的目标检测基准结果。我们采用Faster R-CNN [32]作为检测方法。在这里，我们关注的是将VGG-16 [41]替换为ResNet-101所带来的改进。检测实现（见附录）在两种模型下是相同的，因此这些提升只能归因于更好的网络。最显著的是，在具有挑战性的COCO数据集上，我们在COCO的标准指标（mAP@[.5, .95]）上获得了6.0%的提升，相当于28%的相对改善。这一提升完全归因于学习到的表示。基于深度残差网络，我们在ILSVRC和COCO 2015比赛的多个赛道上获得了第一名：ImageNet检测、ImageNet定位、COCO检测和COCO分割。详细信息见附录。

精读

方法的泛化能力：我们的模型在不同的识别任务上都表现得很好，能够适应其他数据集的需求。
目标检测任务：我们在PASCAL VOC 2007和2012，以及COCO数据集上进行了目标检测的基准测试，采用了Faster R-CNN作为检测框架。
模型改进：我们将VGG-16网络替换成了ResNet-101网络，进行比较。在这两个网络的检测实现是相同的，因此提升的效果完全是因为网络结构本身的优势。
COCO数据集上的提升：在COCO数据集上，我们得到了6.0%的提升，这意味着相对提升了28%。这种提高主要得益于ResNet网络更好的特征表示能力。
比赛成绩：基于深度残差网络，我们在2015年的ILSVRC和COCO比赛中获得了多个赛道的第一名，包括ImageNet检测、ImageNet定位、COCO检测和COCO分割任务。