KNN,K-means算法

1.KNN算法详解

1.1 概述

k临近算法可以解释为：近朱者赤近墨者黑。以下图为例，当K=3时，意味着距离绿点最近的3个点具有投票权，他们将会决定绿点的属性。

决定投票权的是点于点之间的距离，基础距离公式为欧拉距离：
$$distance=\sqrt{\sum _{i=1}^n(X_i^a-X_i^b{)}^2}$$
通过python代码，实现K临近算法的原理：

import numpy as np
import matplotlib.pyplot as plt

# x_train = np.random.uniform(1,10,[10,2])
x_train=np.array([ [8.08742361, 4.77729969],
                   [9.00569228, 6.79223614],
                   [7.21673623, 5.88038928],
                   [7.90739252, 8.49221576],
                   [7.0118063 , 8.23759092],
                   [2.37031554, 7.95508138],
                   [9.47544997, 2.4315193 ],
                   [8.88675088, 8.62900198],
                   [4.7545953 , 5.48956057],
                   [5.28915893, 1.80792096]])
y_train = np.array([1,0,0,0,0,1,1,0,1,1])

plt.scatter(x_train[y_train==0,0], x_train[y_train==0,1], color='g')
plt.scatter(x_train[y_train==1,0], x_train[y_train==1,1], color='b')
plt.scatter(x=5, y=5, color='r')

plt.show()

为了探究上述点中的红色点属于哪一类，首先需要计算其他各个点到红色点的距离。

distance = [sqrt(np.sum((x_train_ - x)**2)) for x_train_ in x_train]
nearest = np.argsort(distance)  # 返回排序结果的索引
# 假设K=3，我们只需要知道离绿点最近距离的3个点是谁，以及他们的属性是什么？
k=6
topk_y = [y_train[i] for i in nearest[:k]]
>>> [1, 0, 1]
# 只需要数一下这个topk_y中储存的数,这里使用Counter
from collections import Counter
votes = Counter(topk_y)
>>>Counter({1: 2, 0: 1})
# 获得结果
votes.most_common(1)[0][0]
>>> 1

1.2 scikit-learn中对KNN的封装

KNN 可以说是一个没有模型的算法，但是也可以说，训练集本身就是模型。

from sklearn.neighbors import KNeighborsClassifier
KNN_classifier = KNeighborsClassifier(n_neighbors=6)  # KNN算法实例化
KNN_classifier.fit(x_train, y_train)  # 训练模型
x = [[5, 5]]
y_predict = KNN_classifier.predict(x)
y_predict[0]
>>> 1

1.3 手写数字的判断

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
digits = datasets.load_digits() # 这里加载了sklearn本身自带的数据
print(digits.DESCR)

以上加载的是手写数字的图片数据。每一张图片代表一个手写的数字也就是一个y值，每一张图片由8*8=64个像素点组成，也就是x值。

x = digits.data
y = digits.target
# 举一个例子
some_digit = x[1]
the_y = y[1] # y=1
some_digit_image = some_digit.reshape(8,8) # 将数据转化为8*8的矩阵
plt.imshow(some_digit_image, cmap=plt.cm.binary) # 绘图
plt.show()

了解数据以后，进入KNN判断的正题

# 我们需要把数据分为两部分，一部分用于训练模型，一部分用于测试模型的好坏
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2)
# 模型训练
from sklearn.neighbors import KNeighborsClassifier
KNN_classifier = KNeighborsClassifier(n_neighbors=3)
KNN_classifier.fit(x_train, y_train)
# 模型预测
y_predict = KNN_classifier.predict(x_test)
# 模型评价
from sklearn.metrics import accuracy_score
accuracy_score(y_test, y_predict)
>>> 0.9833333333333333 表示有98.3的准确率

1.4 其他参数

1.4.1 weights参数

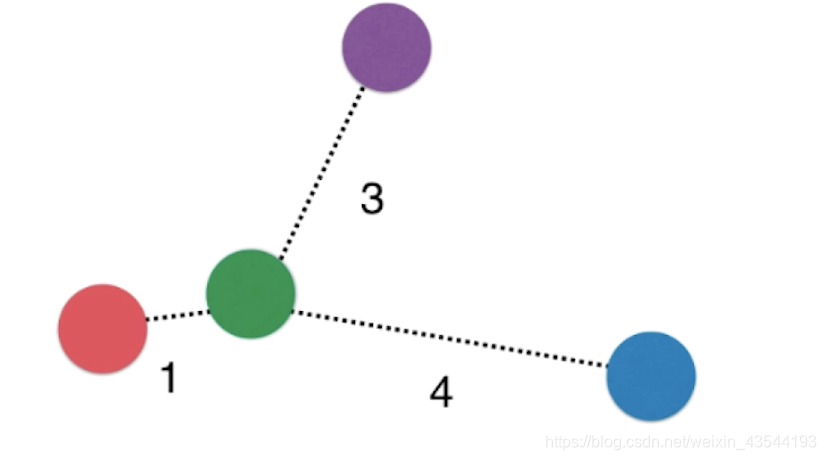
在以上这个图片中，3和4如果是一类，两票可以决定绿点的属性。但事实上，绿点应该是属于红色类。为了解决这个问题，应当赋予距离一个权重，越近权重越高。

1.4.2 超参数p，明可夫斯基距离

$$(\sum _{i=1}^n|X_i^a-X_i^b{|}^p{)}^{1/p}$$
当p=1是，就是曼哈顿距离，当p=2时，就是欧拉距离。

1.4.3 哪种参数合适？网格搜索

# 这里以寻找最好的k值和最好的p值为例子
%%time
from sklearn.metrics import accuracy_score
best_score = 0.0
best_k = -1
best_p = -1
for k in range(1,11):
    for p in range(1,6):
        knn = KNeighborsClassifier(n_neighbors=k)
        knn.fit(x_train, y_train)
        score = knn.score(x_test, y_test)
        if score > best_score:
            best_score = score
            best_p = p
print('best_p = ', best_p)
print('best_k = ', best_k)
print('best_score = ', best_score)

Out:
CPU times: user 38.9 s, sys: 88.5 ms, total: 39 s
Wall time: 39.1 s
GridSearchCV(cv=None, error_score=nan,
             estimator=KNeighborsClassifier(algorithm='auto', leaf_size=30,
                                            metric='minkowski',
                                            metric_params=None, n_jobs=None,
                                            n_neighbors=5, p=2,
                                            weights='uniform'),
             iid='deprecated', n_jobs=None,
             param_grid=[{'n_neighbors': [1, 2, 3, 4, 5, 6, 7, 8, 9, 10],
                          'weights': ['uniform']},
                         {'n_neighbors': [1, 2, 3, 4, 5, 6, 7, 8, 9, 10],
                          'p': [1, 2, 3, 4, 5], 'weights': ['distance']}],
             pre_dispatch='2*n_jobs', refit=True, return_train_score=False,
             scoring=None, verbose=0)

sklearn提供了更强大的网格搜索函数Grid Search

%%time
param_grid = [
    {
        'weights':['uniform'],
        'n_neighbors':[i for i in range(1,11)]
    },
    {
        'weights':['distance'],
        'n_neighbors':[i for i in range(1,11)],
        'p':[i for i in range(1,6)]
    }
]
knn = KNeighborsClassifier()
from sklearn.model_selection import GridSearchCV
grid_search = GridSearchCV(knn, param_grid)
grid_search.fit(x_train, y_train)
print(grid_search.best_estimator_)
	
	Out:
	KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
                     metric_params=None, n_jobs=None, n_neighbors=5, p=2,
                     weights='uniform')

GridSearchCV(knn, param_grid, n_jobs=-1, verbose=2)，这里面n_jobs是计算的时候的使用的核数，verbose是显示计算的过程。

1.5 数据归一化（normalization）

最值归一化
把所有的数据映射到0-1之间，缺点是受到边界影响较大。
$$x_{scale}=\frac{x-x_{min}}{x_{max}-x_{min}}$$

均值方差归一化
所有的数据归一到均值为0，方差为1的正太分布中
$$x_{scale}=\frac{x-x_{min}}{s}$$

from sklearn.preprocessing import StandardScaler
standardScalar = StandardScaler()
standardScalar.fit(x_train)
standardScalar.mean_
standardScalar.scale_ # 方差
standardScalar.transform(x_train)

2. KNN聚类

KNN均值聚类的算法研究网上有很多了，我之后再写

2.1 KNN缺点和调优

首先，K均值算法有以下的缺点：

	- 需要人工设定K值
	- K均值只能是局部最优解，受到初始值的影响
	- 噪点影响很大
	- 样本只能划分到单一的分类

1. 离群点和少量的噪声数据会对均值产生影响，聚类簇的中心点会显著的偏移，因此在使用KNN均值算法之前，要对数据进行归一化和预处理。
2. K值的选择是K均值算法的主要缺点，经验是采用手肘法，尝试不同的K值并将其损失函数华城折线，认为出现损失函数快速下降的拐点处就是最好的K值。
3. 核聚类算法，是通过一个非线形的映射，将输入空间中的数据点映射到高维度的数据空间，在高纬空间中，数据点可能更加的线性可分。

2.2 模型的改进

2.2.1 初始聚类中心改进：K-means++

假设选择了n个初始值，在选择第n+1个初始值的时候，距离当前n个初始值距离更远的点会有更高的概率被选择为第n+1个初始值

2.2.2 K数量的改进：ISODATA

核心的思想是，如果有一个类其中的样本数量过少，则删除改类别(需要设定阈值$N_{min}$）。如果某个类的分散程度过大，则将其分为两个类（需要设定阈值$Sigma$）。如果某两个类的距离过近，则合并为一个(需要设定阈值$D_{min}$)。