题解：Charm Bracelet（基本0-1背包）

最新推荐文章于 2024-11-03 19:35:00 发布

嘘......

最新推荐文章于 2024-11-03 19:35:00 发布

阅读量449

点赞数

CC 4.0 BY-SA版权

分类专栏：杂七杂八

本文链接：https://blog.youkuaiyun.com/weixin_43540515/article/details/99549448

杂七杂八专栏收录该内容

151 篇文章

订阅专栏

本文探讨了一个经典的计算机科学问题——背包问题。通过一个具体的案例，即Bessie在珠宝店选择魅力手链的魅力，展示了如何在重量限制下最大化魅力的总吸引力。文章详细解释了使用动态规划解决此问题的方法，包括输入输出格式、核心算法步骤和示例。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

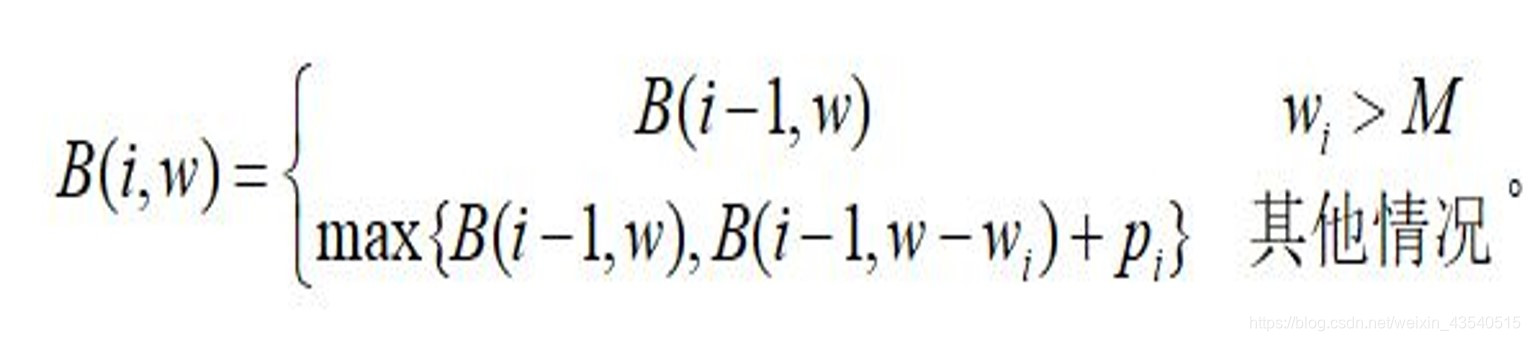
在这里插入图片描述

Bessie has gone to the mall’s jewelry store and spies a charm bracelet. Of course, she’d like to fill it with the best charms possible from the N (1 ≤ N ≤ 3,402) available charms. Each charm i in the supplied list has a weight Wi (1 ≤ Wi ≤ 400), a ‘desirability’ factor Di (1 ≤ Di ≤ 100), and can be used at most once. Bessie can only support a charm bracelet whose weight is no more than M (1 ≤ M ≤ 12,880).
Given that weight limit as a constraint and a list of the charms with their weights and desirability rating, deduce the maximum possible sum of ratings.

Input

Line 1: Two space-separated integers: N and M
Lines 2…N+1: Line i+1 describes charm i with two space-separated integers: Wi and Di

Output
Line 1: A single integer that is the greatest sum of charm desirabilities that can be achieved given the weight constraints
```
  Sample Input
  4 6
  1 4
  2 6
  3 12
  2 7

  Sample Output
  23
```

#include<iostream> 
#include<string>
#include<cstring>
#include<algorithm>
using namespace std;
int v[2000010];//重量为i的子集时的最大价值 
int main()
{
 int n,w,wi,vi;
 cin>>n>>w;
 memset(v,0,sizeof(v));
 for(int i=1;i<=n;i++)
 {
  cin>>wi>>vi;
  for(int j=w;j>=wi;j--)
   v[j]=max(v[j],v[j-wi]+vi);
 }
 cout<<v[w];
 return 0;
}