python根据f(x)绘图（二维）

11FIGHT11

已于 2022-09-30 12:21:59 修改

阅读量1k

点赞数

文章标签： python numpy 机器学习

于 2022-09-30 09:31:48 首次发布

本文链接：https://blog.youkuaiyun.com/weixin_43490216/article/details/127114483

版权

本文介绍了如何使用Python的matplotlib库绘制二维函数图像，包括基本的x^4函数、平移后的x^4函数以及带积分的函数图像。示例代码详细展示了如何生成点列、计算函数值以及调整图像样式和大小。同时，展示了在同一图表上绘制多个函数图像的方法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

python根据函数f(x)绘图（二维）

1.加载相关库
2.根据有效范围生成点列x,并根据f(x)生成对应的点列y
3.绘制图像

f(x)=x^4

import matplotlib.pyplot as plt
import numpy as np
x=np.linspace(0,1,100)#在0,1内等间隔生成100个点列
y=[xi*xi*xi*xi for xi in x]
plt.plot(x,y,label='f(x)=x^4',color=(0,1,1))
plt.legend(title='function',loc='upper right')

基础幂函数

2.f(x)=(x-0.4)^4

import matplotlib.pyplot as plt
import numpy as np
import math
x=np.linspace(0,1,100)#在0,1内等间隔生成100个点列
y=[math.pow(xi-0.4,4) for xi in x]
%matplotlib inline    
sns.set_style('white')#默认'darkgrid':网格帮助图作为定量信息的查找表
plt.rcParams['figure.figsize'] = (12, 8)#设置figure_size尺寸
plt.plot(x,y,label='f(x)=(x-0.4)^4',color=(0,1,1))
plt.legend(title='function',loc='upper right')

中级幂函数
3.f(x)= $\frac{(x-0.4)^4}{\int_{0}^{1}(x-0.4)^4dx}$

import matplotlib.pyplot as plt
import numpy as np
import math
import random
x=np.linspace(0,1,100)
power=4
t=0.4
sum_=(math.pow(0.6,5)-math.pow(-0.4,5))/5
y=[math.pow(xi-t,power)/sum_ for xi in x]
%matplotlib inline    
sns.set_style('white')#默认'darkgrid':网格帮助图作为定量信息的查找表
plt.rcParams['figure.figsize'] = (12, 8)#设置figure_size尺寸
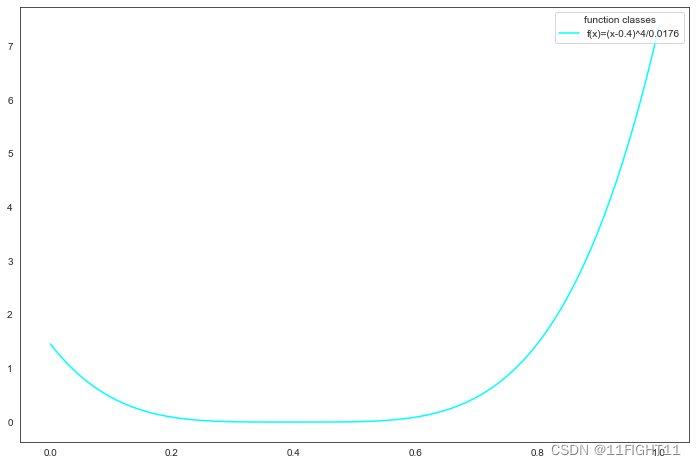
plt.plot(x, y,label='f(x)=(x-0.4)^4/0.0176',color='pink')
plt.legend(title="function classes",loc='upper right')
plt.show()

带积分幂函数

参考文献
1.Markdown KaTex 积分符号
2.Markdown公式笔记(一)：字母上下标和分数表示

附加-一多种曲线绘制在一张图上

import matplotlib.pyplot as plt
import numpy as np
x=np.linspace(0,1,100)
f1=[xi*xi for xi in x]
f2=[xi*xi*xi*xi for xi in x]
f3=[math.pow(xi-t,power) for xi in x]
sum_=(math.pow(0.6,5)-math.pow(-0.4,5))/5
f4=[math.pow(xi-t,power)/sum_ for xi in x]
#plt.plot(x,f1,label='f(x)=x^2',color=(0,1,1))
plt.plot(x,f2,label='f(x)=x^4',color=(0,0,1))
plt.plot(x,f3,label='f(x)=(x-0.4)^4',color=(0,0,1))
#plt.plot(x,f4,label='f(x)=(x-0.4)^4/0.0176',color=(0,0.5,0.5))
plt.legend(title='function',loc='upper right')

import matplotlib.pyplot as plt
import numpy as np
x=np.linspace(0,1,100)
f1=[xi*xi for xi in x]
f2=[xi*xi*xi*xi for xi in x]
f3=[math.pow(xi-t,power) for xi in x]
sum_=(math.pow(0.6,5)-math.pow(-0.4,5))/5
f4=[math.pow(xi-t,power)/sum_ for xi in x]
#plt.plot(x,f1,label='f(x)=x^2',color=(0,1,1))
#plt.plot(x,f2,label='f(x)=x^4',color=(0,0,1))
plt.plot(x,f3,label='f(x)=(x-0.4)^4',color=(0,1,0))
plt.plot(x,f4,label='f(x)=(x-0.4)^4/0.0176',color=(0,1,1))
plt.legend(title='function',loc='upper right')