机器学习笔记---朴素贝叶斯算法

1.朴素贝叶斯算法

1.1基础导入

先验概率：根据个人的历史经验所推测出来的概率。

后验概率：通过贝叶斯公式推断后得到的结果。

极大后验概率估计：在所有的后验概率中选择最大的一个。

极大似然估计：估计使得当前已知结果最有可能发生的模型参数值。

1.2 朴素贝叶斯

贝叶斯公式：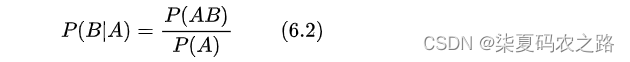

 

 

 

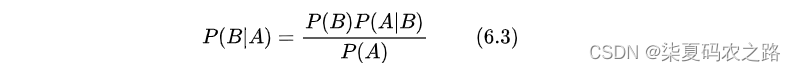
朴素贝叶斯算法所接受的特征输入都是离散型特征（Discrete Features），也就非连续性的特征取值，例如基于词袋模型的文本特征表示等。 

 思考：

当训练集不充分的情况下，某个维度的条件概率确实时该怎么处理。（如果某个条件，训练集不存在这个情况，而在测试的数据样本中却存在这种情况，那么条件会被看着是0，那么在预测的时候将会产生误差）

• 平滑处理：在各个估计中加入一个平滑项。

 

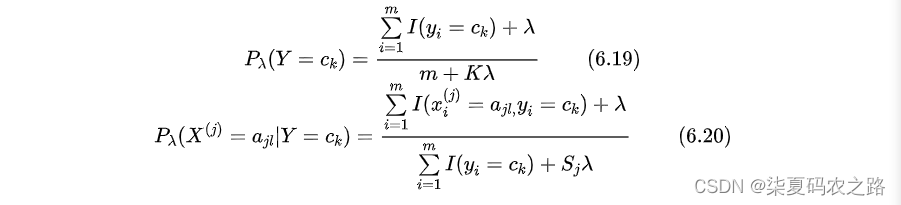
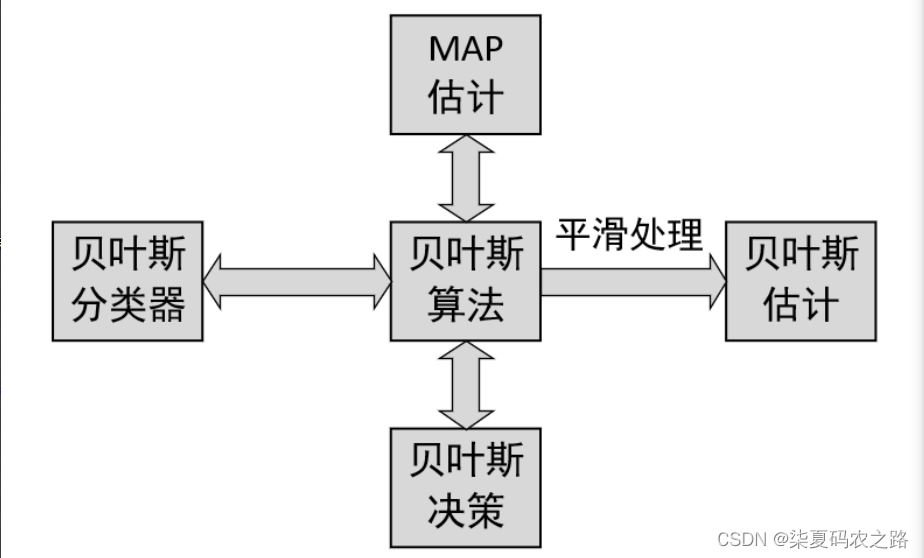
 2.朴素贝叶斯的实现

2.1 特征计数的实现

对两个重要计数器初始化

class MyBayes(object):
 
     def __init__(self, alpha=1.0): #初始化平滑项系数alpha
         self.alpha = alpha 
 
     def _init_counters(self):
         self.class_count_ = np.zeros(self.n_classes, dtype=np.float64) #初始化形状为n_classes的全零向量，n_classes表示分类的类别数量
         self.category_count_ = [np.zeros((self.n_classes, 0))
                                 for _ in range(self.n_features_)]   #category_count初始化了一个n_features元素列表，n_features表示数据集特征维度数量，

 实现各个类别及特征分布的统计

     def _count(self, X, Y): #Y是原始标签经过one-hot编码后的心事
         def _update_cat_count(X_feature, Y, cat_count, n_classes):
             for j in range(n_classes):  # 遍历每个类别
                 mask = Y[:, j].astype(bool)  # 取每个类别下对应样本的索引
                 counts = np.bincount(X_feature[mask])  # 统计当前类别下，特征X_feature中各个取值下的数量
                 indices = np.nonzero(counts)[0]
                 cat_count[j, indices] += counts[indices]
                 
         self.class_count_ += Y.sum(axis=0)  # Y: shape(n,n_classes)   Y.sum(): shape(n_classes,)  
         self.n_categories_ = X.max(axis=0) + 1
 
         for i in range(self.n_features_):  # 遍历每个特征
             X_feature = X[:, i]  # 取每一列的特征
             self.category_count_[i] = np.pad(self.category_count_[i],
                                              [(0, 0), (0, self.n_categories_[i])],
                                              'constant') 
             _update_cat_count(X_feature, Y,self.category_count_[i],self.n_classes)

2.2 先验概率的实现

     def _update_class_prior(self):
         #计算各个类别的先验概率
         self.class_prior_ = (self.class_count_ + self.alpha) /  # shape: [n_classes, ] 
                             (self.class_count_.sum() + self.n_classes * self.alpha)

2.3 条件概率的实现

     def _update_feature_prob(self):
         feature_prob = []
         for i in range(self.n_features_):  # 遍历 每一个特征
             smoothed_cat_count = self.category_count_[i] + self.alpha
             smoothed_class_count = self.category_count_[i].sum(axis=1) +        
                                    self.category_count_[i].shape[1] * self.alpha
             cond_prob = smoothed_cat_count / smoothed_class_count.reshape(-1, 1)
             feature_prob.append(cond_prob)
         self.feature_prob_ = feature_prob
         # feature_prob_ 为一个包含有n_features_个元素的列表，每个元素的shape为 (self.n_classes,特征取值数)

2.4 模型拟合实现

贝叶斯算法来说，所谓的模型拟合就是计算先验概率和条件概率。在实现这部分代码之后，再通过一个函数将整个过程串起来即可，代码如下：

     def fit(self, X, y):
         #将标签转换为one-hot编码形式的标签值，形状为[n,n_classes]
         self.n_features_ = X.shape[1]
         labelbin = LabelBinarizer()  
         Y = labelbin.fit_transform(y) 
         #记录原始的标签类别
         self.classes_ = labelbin.classes_  
         #处理当数据集为二分类时fit_transform处理后的结果并不是one-hot形式，需要添加一列来转换成one-hot形式
         if Y.shape[1] == 1: 
            Y = np.concatenate((1 - Y, Y), axis=1) 
         #获取数据集的类别数量
         self.n_classes = Y.shape[1]
         self._init_counters()  # 初始化计数器
         self._count(X, Y)  # 对各个特征的取值情况进行计数，以计算条件概率等
         self._update_class_prior()
         self._update_feature_prob()
         return self

2.5 后验概率的实现

在完成模型的拟合过程后，对于新输入的样本来说其最终的预测结果则取决于对应的极大后验概率。

 1     def _joint_likelihood(self, X):
 2         if not X.shape[1] == self.n_features_:
 3             raise ValueError("Expected input with %d features, got %d instead"
 4                              % (self.n_features_, X.shape[1]))
 5         jll = np.ones((X.shape[0], self.class_count_.shape[0]))  # 用来累积条件概率
 6         for i in range(self.n_features_):
 7             indices = X[:, i]  # 取对应的每一列特征
 8             if self.feature_prob_[i].shape[1] <= indices.max():
 9                 raise IndexError(f"测试集中的第{i}个特征维度的取值情况"
10                                  f" {indices.max()} 超出了训练集中该维度的取值情况！")
11             jll *= self.feature_prob_[i][:, indices].T  # 取每个特征取值下对应的条件概率，并进行累乘
12         total_ll = jll * self.class_prior_  # 条件概率乘以先验概率即得到后验概率
13         return total_ll

注意：
在文本向量化中对于考虑词频的词袋模型来说，其向量表示并不能直接使用于这里实现的贝叶斯模型。因为此时训练集词表中每个词出现的次数并不是该特征维度对应的取值情况数，而是表示的频次。例如在训练集中“客栈”这个词出现的最大次数为10，那么模型在拟合过程中就会认为“客栈”这个维度的特征取值有10种情况，并以此进行建模；但是当测试集中的某个样本里“客栈”这个词出现的频次为11时，那么模型便会认为该维度多了一种取值情况，进而无法取到对应的条件概率。所以在8-10行中加了对应的判断条件。

在实现完个样本后验概率的计算结果后，最后一步需要完成的便是极大化操作，即从所有后验概率中选择最大的概率值对应的类别作为该样本的预测类别即可。

1     def predict(self, X, with_prob=False):
2         from scipy.special import softmax
3         jll = self._joint_likelihood(X)
4         y_pred = self.classes_[np.argmax(jll, axis=1)]    #极大化后验概率
            #根据对应的参数来返回预测后的结果。
5         if with_prob:
6             prob = softmax(jll)
7             return y_pred, prob
8         return y_pred

2.6 邮件分类案例

 1 def test_spam_classification():
 2     x_train, x_test, y_train, y_test = load_data()
 3     model = MyBayes(alpha=1.0)
 4     model.fit(x_train, y_train) #训练模型
 5     y_pred = model.predict(x_test)
 6     logging.info(f"My Bayes 运行结果：")
 7     logging.info(classification_report(y_test, y_pred)) #分类评估
 8 
 9     model = CategoricalNB()
10     model.fit(x_train, y_train)
11     y_pred = model.predict(x_test)
12     logging.info(f"CategoricalNB 运行结果：")
13     logging.info(classification_report(y_test, y_pred))

3.多项朴素贝叶斯

3.1 算法原理

 3.2 多项贝叶斯实现

 特征计数实现

1 class MyMultinomialNB(object):
2   def __init__(self, alpha=0):
3         self.alpha = alpha
4         self._ALPHA_MIN = 1e-10
5     def _init_counters(self, ):
6         self.class_count_ = np.zeros(self.n_classes, dtype=np.float64)
7         self.feature_count_ = np.zeros((self.n_classes, 
8                               self.n_features_),dtype=np.float64)

feature_count_ = [[ 6. 31. 36.],[44. 22. 28.],[19. 10. 14.]]

对样本类别和特征分布进行计数了：

     def _count(self, X, Y):
         self.class_count_ += Y.sum(axis=0) # shape [n_classes,]
         # 计算得到每个类别下的样本数量
         self.feature_count_ += np.dot(Y.T, X)  # [n_classes,n] @ [n,n_features_]

4.高斯朴素贝叶斯

根据Categorical贝叶斯和Multinomial贝叶斯算法的原理可知，前者只能用于处理类别型取值的特征变量，而后者的初衷也是为了处理包含词频的文本向量表示（尽管从结果上看也适用于类似tf-idf这样的连续型特征）。所谓高斯贝叶斯指的便是假定样本每个特征维度的条件概率均服从高斯分布，进而再根据贝叶斯公式来计算得到新样本在某个特征分布下其属于各个类别的后验概率，最后通过极大化后验概率来确定样本的所属类别。

4.1 算法原理

4.2 高斯叶斯实现

 参数初始化实现

 1 class MyGaussianNB(object):
 2     def __init__(self, var_smoothing=1e-9):
 3         self.var_smoothing = var_smoothing
 4 
 5     def _init_counters(self, X, y):
 6         self.classes_ = np.sort(np.unique(y))
 7         n_features = X.shape[1]
 8         n_classes = len(self.classes_)
 9         self.mu_ = np.zeros((n_classes, n_features))
10         self.sigma2_ = np.zeros((n_classes, n_features))
11         self.class_count_ = np.zeros(n_classes, dtype=np.float64)
12         self.class_prior_ = np.zeros(len(self.classes_), dtype=np.float64)

 模型拟合实现

 1     def fit(self, X, y):
 2         self._init_counters(X, y)
 3        self.epsilon_ = self.var_smoothing * np.var(X, axis=0).max()
 4         for i, y_i in enumerate(self.classes_):  # 遍历每一个类别
 5             X_i = X[y == y_i, :]  # 取类别y_i对应的所有样本
 6             self.mu_[i, :] = np.mean(X_i, axis=0)  # 计算期望
 7             self.sigma2_[i, :] = np.var(X_i, axis=0)  # 计算方差
 8             self.class_count_[i] += X_i.shape[0]  # 类别y_i对应的样本数量
 9         self.sigma2_ += self.epsilon_
10         self.class_prior_ = self.class_count_ / self.class_count_.sum()
11         return self

后验概率的实现

 1     def _joint_likelihood(self, X):
 2         joint_likelihood = []
 3         for i in range(np.size(self.classes_)):
 4             jointi = np.log(self.class_prior_[i])  # shape: [1,]
 5             n_ij = - 0.5 * np.sum(np.log(2. * np.pi * self.sigma2_[i, :]))
 6             n_ij -= 0.5 * np.sum(((X - self.mu_[i, :]) ** 2) /
 7                                  (self.sigma2_[i, :]), 1)  # shape: [n_samples,]
 8             joint_likelihood.append(jointi + n_ij)  # [[n_samples,1],..[n_samples,1]]
 9         joint_likelihood = np.array(joint_likelihood).T  # [n_samples,n_classes]
10         return joint_likelihood

在实现每个样本后验概率的计算结果后，最后一步需要完成的便是极大化操作，即从所有后验概率中选择最大的概率值对应的类别作为该样本的预测类别即可。

1     def predict(self, X, with_prob=False):
2         from scipy.special import softmax
3         jll = self._joint_likelihood(X)
4         y_pred = self.classes_[np.argmax(jll, axis=1)]
5         if with_prob:
6             prob = softmax(jll)
7             return y_pred, prob
8         return y_pred

以上信息均来源于月来客栈，个人学习记录，如有侵权请联系删除！！！！