数据结构与算法Python版 08 算法之排序篇

排序简介

常见的十大排序算法如下所示，本章节会例举6种常见且易于掌握的排序算法：

算法名称	平均时间复杂度	最好情况	最坏情况	空间复杂度	排序方式	稳定性
冒泡排序	O(n²)	O(n)	O(n²)	O(1)	in-place	稳定
选择排序	O(n²)	O(n²)	O(n²)	O(1)	in-place	不稳定
插入排序	O(n²)	O(n)	O(n²)	O(1)	in-place	稳定
希尔排序	O(n log n)	O(n log n)	O(n log² n)	O(1)	in-plcae	不稳定
归并排序	O(n log n)	O(n log n)	O(n log n)	O(n)	out-place	稳定
快速排序	O(n log n)	O(n log n)	O(n²)	O(log n)	in-plcae	不稳定
堆排序	O(n log n)	O(n log n)	O(n log n)	O(1)	in-plcae	不稳定
计数排序	O(n + k)	O(n + k)	O(n + k)	O(k)	out-place	稳定
桶排序	O(n + k)	O(n + k)	O(n²)	O(n + k)	out-place	稳定
基数排序	O(n + k)	O(n + k)	O(n + k)	O(n + k)	out-place	稳定

关于排序算法的3大基础知识：

• 稳定性：示例，排序前红色3在蓝色3前面，如果排序完成后位置没有发生改变则该排序算法是稳定的：

  • 稳定：1，2，3，3，5
  • 不稳定：1，2，3，3，5

• 有序区和无序区：在排序算法中，会将一个序列分为2大区，如下所示：

  [1, 2, 3, | 28, 11, 43]
  ----------  ----------
    有序区        无序区
  

• 原地排序：原地排序是指在原序列中进行数据项排列，不用开辟额外内存空间

  非原地排序则需要生成新的序列，来存储排列好的数据项，空间复杂度会增加

冒泡排序

冒泡排序（Bubble Sort）是一种简单的排序算法。

这种排序算法是基于比较的算法，每次比较2个相邻数据项并进行交换。

该算法不适合大型数据集，因为其平均和最坏情况复杂度为 Ο(n²)，其中n是项目数。

代码及注释如下：

def bubbleSort(seq):
    # ❶
    for i in range(len(seq) - 1):
        # ❷
        tag = False
        # ❸
        for j in range(len(seq) - (i + 1)):
            if seq[j] > seq[j + 1]:
                seq[j], seq[j + 1] = seq[j + 1], seq[j]
                tag = True
        if not tag:
            break
            
if __name__ == "__main__":
    lst = [2, 1, 3, 4, 5, 6, 7, 8, 9]
    bubbleSort(lst)
    print(lst)

❶：我们认为最后1个数据项不用排序，故循环次数是 len(seq) - 1，每一次外层循环都会令有序区数据项 + 1

❷：一个标志位，用于判定是否还需要继续进行排序

❸：内层循环只会遍历无序区数据项，i 是外层循环次数， + 1代指seq最后1个数据项，即不用排序的数据项

如果不加该标志位，则会产生许多重复的且无用的排序，因此该标志位算是一种优化手段。

选择排序

选择排序（Selection Sort）会将序列分为2部分，有序区和无序区。

它的工作原理：首先在无序区中找到最小（大）数据项，存放到有序区的起始位置，然后，再从剩余无序区中继续寻找最小（大）数据项，然后放到有序区的末尾。

以此类推，直到所有数据项均排序完毕。

该算法不适合大型数据集，因为其平均和最坏情况复杂度为 Ο(n²)，其中n是项目数。

代码及注释如下：

def selectionSort(seq):
    # ❶
    for i in range(len(seq) - 1):
        # ❷
        minIndex = i
        # ❸
        for j in range(i + 1, len(seq)):
            # ❹
            if seq[minIndex] > seq[j]:
                minIndex = j
        # ❺
        if minIndex != i:
            seq[i], seq[minIndex] = seq[minIndex], seq[i]


if __name__ == '__main__':
    lst = [4, 1, 0, 2, 3]
    selectionSort(lst)
    print(lst)

❶：我们认为最后1个数据项不用排序，故循环次数是 len(seq) - 1，每一次外层循环都会令有序区数据项 + 1

❷：将当前被外层循环遍历的数据项当做最小值，并记录其索引位置

❸：循环所有无序区数据项

❹：判断当前被遍历的无序区数据项是否小于以设定的最小值数据项，如果是则更新

❺：交换最小值数据项与外层循环被遍历数据项的位置

插入排序

插入排序（Inster Sort）类似于打扑克牌，先会构建出一个有序区，再遍历无序区数据项并将其插入到有序区中合适的位置。

该算法不适合大型数据集，因为其平均和最坏情况复杂度为 Ο(n²)，其中n是项目数。

代码及注释如下：

def insertSort(seq):
    # ❶
    for i in range(1, len(seq)):
        # ❷
        currentItem = seq[i]
        # ❸
        prevItemIndex = i - 1
        # ❹
        while prevItemIndex >= 0 and seq[prevItemIndex] > currentItem:
        # ❺
            seq[prevItemIndex + 1] = seq[prevItemIndex]
            prevItemIndex -= 1
        seq[prevItemIndex + 1] = currentItem


if __name__ == "__main__":
    lst = [1, 4, 2, 3, 0]
    insertSort(lst)
    print(lst)

❶：外层循环从索引1处开始向后遍历，即我们认为有序区默认有1个数据项

❷：拿到当前的数据项，即有序区最后一个数据项

❸：拿到有序区前一个数据项的索引，这里就是插入位置，当无序区被遍历数据项小于有序区最后一个数据项，就插入到这里

❹：条件1：如序列为[1, 2, 3 | 0, 9, 8, 10]，0如果想要插入1前面，索引就变成了-1，而-1位置是序列中最后位置，这样就会插入失败，故该条件确保不会出现负向索引

条件2：规定什么时候进行插入，当然是被遍历的无序区数据项小于有序区最后一个数据项时才进行插入

❺：寻找插入位置

希尔排序

希尔排序（Shell Sort）是插入排序的一种，它是针对直接插入排序算法的改进。

希尔排序又称缩小增量排序，因 DL.Shell 于 1959 年提出而得名。

它通过比较相距一定间隔的数据项来进行，各趟比较所用的距离随着算法的进行而减小，直到只比较相邻数据项的最后一趟排序为止，是首次突破O(n²)的排序算法。

该算法对于中等规模的数据集非常有效，因为该算法的平均和最坏情况复杂度取决于间隙序列，最著名的是 Ο(n)，其中 n 是项目的数量。最坏情况下的空间复杂度是 O(n)。

首先，我们有一个长度为8的序列，我们需要对其 // 2，得到一个值是4，这个值叫做gap值。

现在，我们将整个序列分为4组，如下图所示，35和14为一组，中间的间隔是4，33和19是一组，中间的间隔也是4，依次类推：

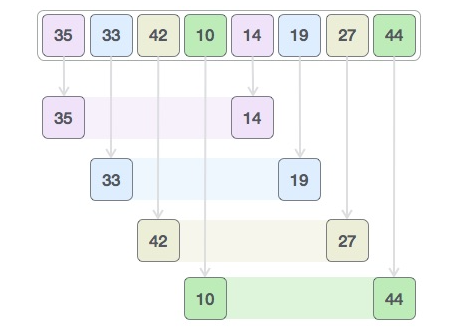
然后我们对这4组中的元素进行插入排序，非常简单，下图是排序完成后的样子：

上次得到的gap值是4，我们再将它 // 2，得到新的gap值，为2。

老规矩，将整个序列分为2组，如下图所示：

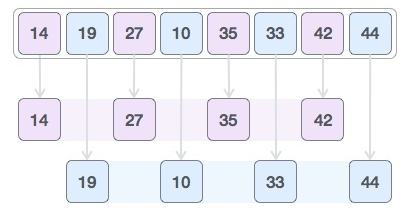
然后，再将这2组中的元素进行插入排序，下图是排序完成之后的样子：

上次的gap值是2，我们再将它 // 2，得到结果是1，继续对这1组进行插入排序，如下图所示：

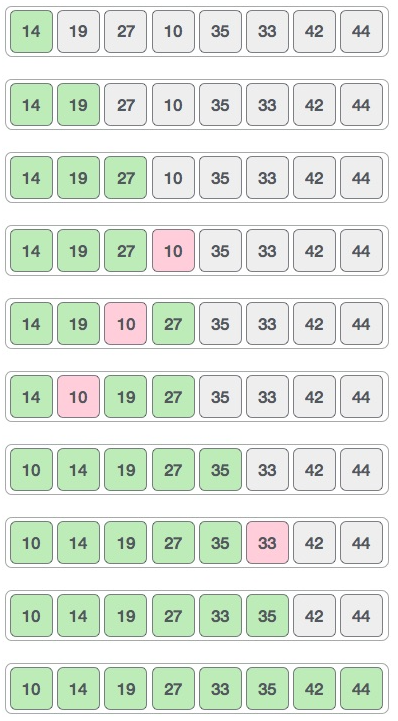
代码及注释如下：

def shellSort(seq):
    # ❶
    currentGap = len(seq) // 2
    # ❷
    while currentGap >= 1:
        # ❸
        for startPosition in range(currentGap):
            gapInsertSort(seq, startPosition, currentGap)
        print("after increments of size %s, the sequence is %s" %
              (currentGap, seq))
        # ❹
        currentGap //= 2


def gapInsertSort(seq, start, gap):
    # ❺
    for i in range(start + gap, len(seq), gap):
        currentItem = seq[i]
        position = i

        while position >= gap and seq[position - gap] > currentItem:
            seq[position] = seq[position - gap]
            position = position - gap

        seq[position] = currentItem


if __name__ == "__main__":
    lst = [35, 33, 42, 10, 14, 19, 27, 44]
    shellSort(lst)
    print(lst)

❶：获取gap值，后续会根据gap值进行分组

❷：死循环，直至所有组都排序完毕

❸：循环，开始进行插入排序

❹：插入排序完毕后，重新进行分组，更新gap值

❺：start + gap是当前需要插排的分组，len(seq)是整体序列长度， gap是跳过的步数，也就是不同的分组，至此开始每一轮的插入排序

归并排序

归并排序（Merge Sort）是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。

归并排序会不断的将序列 // 2，直至每个序列仅包含1个数据项，然后再将小序列排序并合并成大序列。

归并排序是一种基于分治技术的排序技术，最坏情况的时间复杂度为 Ο(n log n)，它是最受尊敬的算法之一。

首先，下面是一个未经历排序的长度为8的序列：

我们不断的将它拆分，直至每个序列中仅有1个数据项：

然后开始进行子序列合并，通过不断的对比每个子序列中的数据项，最终将它们合并成1个大的序列：

代码及注释如下：

def mergeSort(seq):
    # ❶
    if len(seq) > 1:

        mid = len(seq) // 2
        leftSeq, rightSeq = seq[:mid], seq[mid:]

        mergeSort(leftSeq)
        mergeSort(rightSeq)

        # ❷
        i = j = k = 0

        while i < len(leftSeq) and j < len(rightSeq):

            # ❸
            if leftSeq[i] < rightSeq[j]:
                seq[k] = leftSeq[i]
                i += 1

            # ❹
            else:
                seq[k] = rightSeq[j]
                j += 1

            k += 1

        # ❺
        while i < len(leftSeq):
            seq[k] = leftSeq[i]
            i, k = i + 1, k + 1

        # ❻
        while j < len(rightSeq):
            seq[k] = rightSeq[j]
            j, k = j + 1, k + 1

    print("merging:", seq)


if __name__ == "__main__":
    lst = [14, 33, 27, 10, 35, 19, 42, 44]
    mergeSort(lst)
    print(lst)

❶：不断的对序列进行拆分，直至每个序列中仅有1个数据项

❷：开始进行排序、对比、合并，i 是左侧序列索引值，j是右侧序列索引值，k是整个大序列索引值

❸：如果左序列被遍历数据项小于右序列被遍历数据项，则整体大序列中左序列数据项排列在前面

如：leftSeq = [0]， rightSeq = [1]， 则大的seq = [0 , 1]

❹：如果右序列被遍历数据项小于左序列被遍历数据项，则整体大序列中右序列数据项排列在前面

如：leftSeq = [1]， rightSeq = [0]， 则大的seq = [0 , 0]

❺：针对❹的情况，要将大seq的[0, 0]变为[0, 1]，因为❹的时候 i 没有 + 1，总之最后要保证：i = 1, j = 1, k = 2

❻：针对❸的情况，因为❸的时候 j 没有 + 1，总之最后要保证：i = 1, j = 1, k = 2

快速排序

快速排序（Quick Sort）最大的特点就是快，使用分治法进行实现。

它的算法步骤是在一个序列中选定任意一个值，作为基准（pivot），然后使用2个指针，从序列的左侧与右侧一起进行数据项检测，每检测1步2个指针距离更进一步。

• 左侧指针用于将比基准值小的数据项排在左侧
• 右侧指针用于将比基准值大的数据项排在右侧

当2个指针重合时代表一趟排序完成，如此排列一轮整个序列就分为了2组，左侧比基准小（左侧各个序列数据项之间也大概率无序），右侧比基准大（右侧各个序列数据项之间也大概率无序）。

再次重复以上的步骤，对左侧或者右侧的列表重新定义基准值，再次进行挑选，直至最后划分为无数个长度为1的小序列时，排序完成。

该算法对于大型数据集非常有效，因为其平均复杂度和最坏情况复杂度分别为O(n log n) 和 O(n² )。

可能动图演示太快了，我们使用图解的形式：

第一趟的基准值是6（随机的）：

接下来继续第2倘，重新定义基准值为3（随机的），重复上面的步骤。

代码及注释如下：

def quickSort(seq):

    def innerQuickSort(seq, left, right):
        if left < right:
            mid = partition(seq, left, right)
            innerQuickSort(seq, left, mid - 1)
            innerQuickSort(seq, mid + 1, right)

    innerQuickSort(seq, 0, len(seq) - 1)

def partition(seq, left, right):
    # ❶
    pivot = seq[left]
    while left < right:
        # ❷
        while right > left and seq[right] >= pivot:
            right -= 1
        seq[left] = seq[right]
        # ❸
        while left < right and seq[left] <= pivot:
            left += 1
        seq[right] = seq[left]

    # ❹
    seq[left] = pivot
    return left

if __name__ == "__main__":
    lst = [54, 26, 93, 17, 77, 31, 44, 55, 20]
    quickSort(lst)
    print(lst)

❶：定义基准值，pivot

❷：右侧指针与左侧指针没有重合，且右侧指针数据项大于基准值则右侧指针左移一位

❸：左侧指针与右侧指针没有重合，且左侧指针数据项小于基准值则左侧指针右移一位

❹：重新定义基准值，本倘遍历完成

此时还可能会出现一个最坏情况：

• 由于pivot我们总是选择在了首位，如果出现传入一个已经有序（升序）的列表，就会发生最坏情况。

• 反之，如果pivot总是选择在末位，如果出现传入一个已经有序（降序）的列表，也会发生最坏的情况。

最坏情况下，时间复杂度将退化O(n²)，加上递归的开销可能比冒泡排序还要慢一点，解决方案是将pivot选择为一个随机位置，如中间。