数据结构与算法Python版 07 算法之搜索篇

线性搜索

顺序查找也被称之为线性查找，因在Python中list的底层为顺序表存储，故我们可以使用index来循环遍历整个列表获得所需要查找的数据项。

它的时间复杂度为O(n)，如果刚好被搜索的数据项排列在最后一个，那么整个查找是非常耗费时间的：

如下所示，如果查找数据项50，将会查找11次：

def seqLinerSearch(seq, findItem):
    idx = 0
    count = 0
    seqLenght = len(seq)
    while idx < seqLenght:
        count += 1
        if findItem == seq[idx]:
            return findItem, count
        idx += 1
    return None, count


if __name__ == "__main__":
    lst = [18, 22, 34, 2, 71, 8, 92, 37, 82, 91, 50]
    result, count = seqLinerSearch(lst, findItem=50)
    print(result, count)

# 50 11

有序的必要性

现在，让我们观察上面的代码是否有什么可以优化的地方。

我们的查找在数据项不存在的情况下总是会遍历完整个列表，导致这个问题的主要原因还是因为传入的列表是无序的。

如上述代码，我们查找数据项53，它总是一遍一遍的进行对比，直至对比完成整个列表发现都没有符合条件的数据项后才会返回，时间复杂度总是为O(n)，所以要针对这个情况进行简单的优化。

如果我们将列表排为有序的状态，当查找到71后，也就发现了没有必要往后查找，故至此直接返回即可。

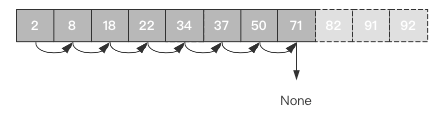
优化策略：

• 列表要有序
• 如果正在遍历的数据项大于被查找的数据项，则代表此列表中没有该数据项

代码实现如下，虽然整体的时间复杂度还是O(n)，但是已经做了很大的优化了：

def seqLinerSearch(seq, findItem):
    idx = 0
    count = 0
    seqLenght = len(seq)
    while idx < seqLenght and seq[idx] <= findItem:
        count += 1
        if findItem == seq[idx]:
            return findItem, count
        idx += 1
    return None, count


if __name__ == "__main__":
    lst = [2, 8, 18, 22, 34, 37, 50, 71, 82, 91, 92]
    result, count = seqLinerSearch(lst, findItem=53)
    print(result, count)

# None 7

注意：排序本身就花费时间，复杂度为O(n log n)

二分搜索

通过上面的2个例子，可以得出一个结论：

对查找来说，保持数据项的有序是十分必要的

那么现在基于这个先决条件，介绍一种查找效率更高的算法，二分查找法。

二分查找的实现理念：每次只查找列表中间元素的值，判定这个中间元素与被查找元素的关系，通过关系将列表进行折半后，继续查找，时间复杂度是O(logn)，如下所示二分查找法与顺序查找的对比图：

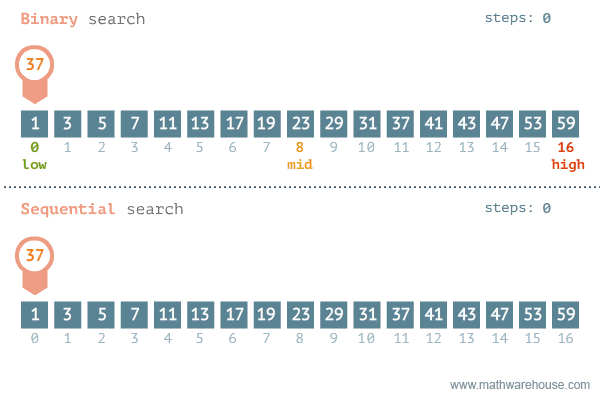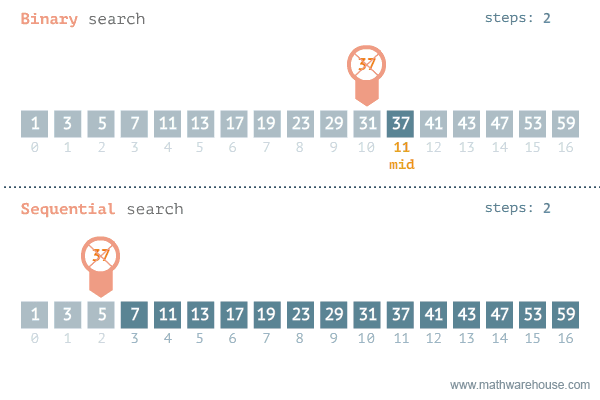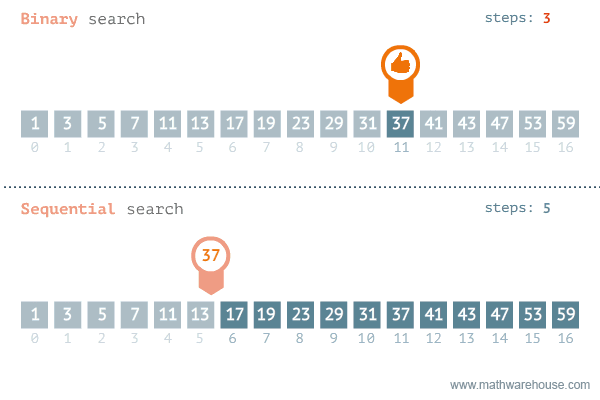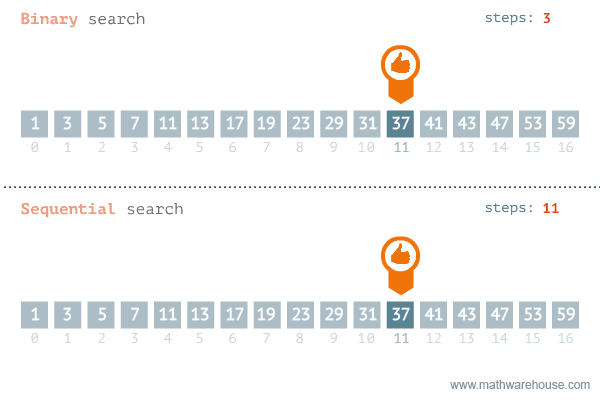
实现二分查找，查找数据项50仅需要3次：

#! /usr/local/bin/python3
# -*- coding:utf-8 -*-

def binarySearch(seq, findItem):
    count = 0
    l_idx = 0
    r_idx = len(seq) - 1

    while l_idx <= r_idx:
        count += 1

        m_idx = (l_idx + r_idx) // 2

        # 如果查找的元素等于当前列表中部索引的元素，则返回
        if findItem == seq[m_idx]:
            return findItem, count

        # 如果查找的元素大于当前列表中部索引的元素，则重新定义左侧索引
        elif findItem > seq[m_idx]:
            l_idx = m_idx + 1

        # 如果查找的元素小于当前列表中部索引的元素，则重新定义右侧索引
        else:
            r_idx = m_idx - 1

    else:
        return None, count


if __name__ == '__main__':
    result, count = binarySearch([2, 8, 18, 22, 34, 37, 50, 71, 82, 91, 92], 50)
    print(result, count)

# 50 3