数据结构与算法Python版 06 算法之递归篇_递归函数baseconversion(num,base)-优快云博客

本文链接：https://blog.youkuaiyun.com/weixin_43422005/article/details/118544908

本文深入探讨了递归算法，包括递归的基本原理、分治策略的三个步骤，如进制转换和汉诺塔问题的递归解决方案。此外，还介绍了贪心策略在找硬币问题中的应用，以及动态规划的概念和优化方案，展示了如何避免重复计算以提高效率。最后，文章通过turtle模块展示了递归在图形绘制中的应用，如分形树和谢尔宾斯基三角形的绘制。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

递归前言

递归（Recursion）相信各位都非常了解了，所以这里就不再详细阐述，具体可参照Python函数章节中的递归函数。

递归三大定律如下：

递归算法必须有一个基本结束条件
递归算法必须能改变问题规模
递归算法必须调用自身

分治策略

分治策略是指将一个大规模的问题分解成更小的相同问题，经过持续分解到最后问题规模小到可以用非常简单直接的方式来解决，或者将一个问题拆分成不同的各个部分，分而解决分而治之。

分治策略一般会经历三个步骤：

划分：此步骤涉及将问题分解为更小的子问题。子问题应该代表原始问题的一部分。这一步通常采用递归方法来划分问题，直到没有子问题可以进一步划分。在这个阶段，子问题本质上变成了原子，但仍然代表了实际问题的一部分
解决：这一步需要解决很多较小的子问题。通常，在此级别上，问题被视为自行“解决”。
合并：当较小的子问题得到解决时，这个阶段会开始递归地组合它们，直到它们合并成出原始问题的解决方案。

进制转换

前面的线性结构（栈）我们实现了一次10进制转换2、8、16进制，如果利用递归函数则整个实现过程又会变的非常简单。

如下所示：

def baseConversion(n, base):
    digits = "0123456789ABCDEF"
    if n < base:
        return digits[n]
    return baseConversion(n // base, base) + digits[n % base]

if __name__ == "__main__":
    print(baseConversion(101, 2))
    print(baseConversion(101, 8))
    print(baseConversion(101, 16))
    
# 1100101
# 145
# 65

汉诺塔

汉诺塔问题是由法国数学家爱德华·卢卡斯在 1883 年提出的。

他的灵感来自一个传说，有一个印度教寺庙，将谜题交给年轻的牧师，在开始的时候，牧师被给予三根杆和一堆 64 个金碟，每个盘比它下面一个小一点。

牧师的任务是将所有 64 个盘子从三个杆中一个转移到另一个。

有两个重要的约束：

一次只能移动一个盘子
不能在较小的盘子顶部上放置更大的盘子。

牧师日夜不停每秒钟移动一块盘子，传说，当他完成工作时，寺庙会变成灰尘，世界将消失。

游戏规则如下图所示：

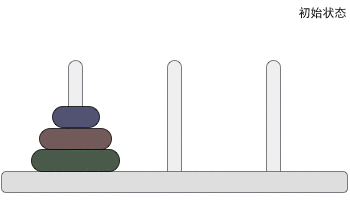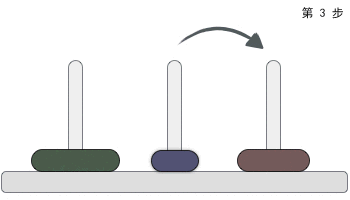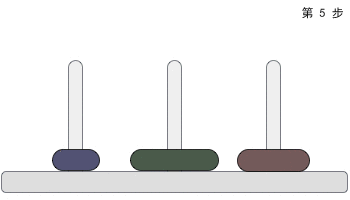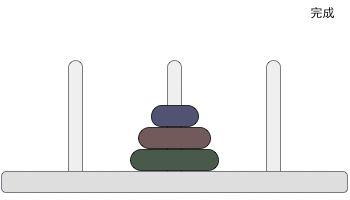
汉诺塔问题- 编程帮

如何用递归法求解呢？我们先对汉诺塔本身的游戏规则进行分析。

在上图中可以看到，s和m型号的圆盘，必须通过C号杆子再坐落到B号杆子上，我们可以将任意数量的非最大号的圆盘看为一整组，而最大号圆盘单独分为一组，总共将圆盘分为2组，并且在移动时按照组来进行划分：

算法如下，如此只要分三步即可：

把n-1个圆盘从柱子A经过C移动到B，但是省略掉到C的步骤，直接到B即可
把第n圆盘（最大的圆盘）从A移动到C
把n-1个圆盘从B经过A移动到C，但是省略掉到A的步骤，直接到C即可

代码如下，先按照3个圆盘求解：

def hanoi(n, a, b, c):
    if n:
        # 从a经过c到b
        hanoi(n - 1, a, c, b)
        # 从a到c
        print("moving from %s to %s" % (a, c))
        # 从b经过a到c
        hanoi(n - 1, b, a, c)


if __name__ == "__main__":
    hanoi(3, "A", "B", "C")

# moving from A to C
# moving from A to B
# moving from C to B
# moving from A to C
# moving from B to A
# moving from B to C
# moving from A to C