算法基础期末考点总结十五——动态规划

我对动态规划这一章的理解，例子太多了。就一章，包括了4个例子，但我觉得矩阵乘法是重点，而且大概率只会求那个数组，这个我通过做题已经掌握了规律，所以这一章我不会讲的太仔细，只会讲一讲数组。

动态规划

首先，动态规划处理的是什么问题？
具有最优子结构的问题。做出一个选择后，问题分解成若干子问题。
什么是动态规划算法的特点？
对每个子问题只求解一次。

钢条切割问题

r是最大化收益，p是价格

s是切割的位置

矩阵链乘

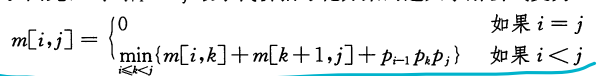
pi pi+1是第i+1个矩阵的规模。
m[i，j]是第i个矩阵乘到第j个矩阵最少的乘法次数

s是分割的位置，如m[1，6] = 3代表1到3和4到6各为一组

最长公共子序列

c[i,j]代表X序列的前i位和Y序列的前j位的最长公共子序列的长度

如果当前读到的两个字符相等，最大公共子序列长度加一，箭头指向斜上；否则，最长公共子序列是左边和上边最大的一个，箭头指向最大的方向。

最优二叉搜索树

对于一颗关键字为n的二叉搜索树，有2n+1种搜索结果。

k是匹配的结果，d是不匹配的结果。
我们定义e[i , j]代表包括ki,…kj,di-1,di,…dj的树的代价，我们要求的即是e[1，n]。
令

则

特别的e[i，i] = pi+qi-1+qi。

e是总代价，w是辅助函数，root是根节点下标。