学习笔记：网络流基础：理解最大流/最小割定理 (蒋炎岩)-优快云博客

本文链接：https://blog.youkuaiyun.com/weixin_43408232/article/details/109818498

课程链接

网络流基础：理解最大流/最小割定理 (蒋炎岩)
https://www.bilibili.com/video/BV1Q7411R7ie

有向图的基本概念：

略

问题引入

给定一个有向图，给定起点s和终点t，我们能否找到一条路径：So easy！
在这里插入图片描述

在这里插入图片描述

我们可以使用DFS,BFS找到路径，只是找到，但是没有给出证明；
也就是为什么路径不存在？DFS和BFS只是方法，并没有在理论上严格证明路径是不存在，我们希望理论上严格证明。

直观感受反例

在下面的图里求解s–>t是否存在路径：
不存在
在这里插入图片描述
为了给出严格证明，先给出所有s开头，t结尾的路径排列：

而在这里面，有些路径是不存在的，比如s->t的有向边
如果存在合法路径，一定满足上述排列

这个证明是严格的，但是存在问题：
在这里插入图片描述
再来看一下DFS/BFS是怎么找不到路径的

在这个问题中，我们利用DFS和BFS的算法，最后是可以把原图上的点分割为S和T的两个集合，如果不存在所求路径，则红色的边是一定不存在，即出发点在S集合，终点在T集合的点，但是可以有反向边。
在这里插入图片描述

引入重要概念：

在这里插入图片描述

割的示例

在这里插入图片描述
这个图的割为2

这个图的割为3

小结

所以我们之所以找不到一条路径是因为图中存在一个大小为0的割
在这里插入图片描述

再来一个问题

DFS和BFS可以帮助我们找到路径，找到1条路径，so easy!
找到k条路径，k>=2呢？BFS和DFS还能解决吗？
在这里插入图片描述

例子

在这里插入图片描述

可以找到一条路径的情况

在这里插入图片描述

可以找到两条路径的情况

在这里插入图片描述

问题的转化

求解它存在多少条路径的问题，可以等价转化为求解下面验证性的判定问题
在这里插入图片描述
首先验证k=1;
成立，则验证k=2;
成立，则验证k=3;
………………
………………
直到k=m+1不成立，这样，我们就求解得到了k的最小值m
这是一种好思路，但是怎么做呢？It is difficult！

那就试试问题的反面

在这里插入图片描述

小结

图中所有割的大小 L决定了可以找到k条路径的上限
我们目前已经找到的路径数m决定了可以找到k条路径的下限
在这里插入图片描述

不相交路径问题的求解

从一个错误的算法开始

在这里插入图片描述
我们可以使用贪心算法，在图中找到一条路径以后，就去掉这条路径，然后接着找下一条，但是问题是，贪心算法去掉的算法是正确的吗？会不会丢了不该丢的？
比如这样

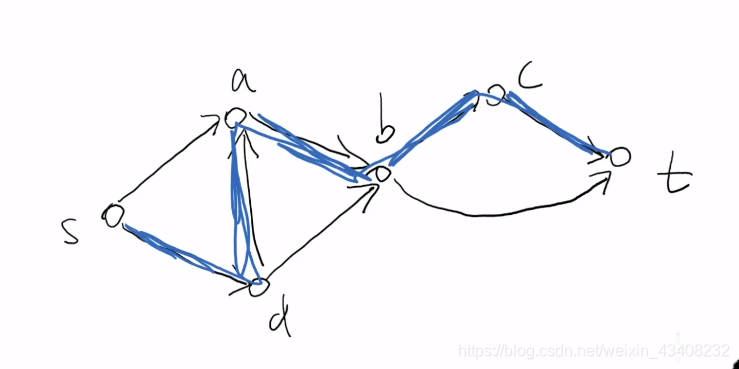
这是同一个图
所以我们在错误的算法

算法的改进

FORD-FULKERSON算法

L. R. FORD, JR. AND D. R. FULKERSON MAXIMAL FLOW THROUGH A NETWORK 原文链接
http://bioinfo.ict.ac.cn/~dbu/AlgorithmCourses/Lectures/FordFulkerson1956.pdf

算法的进一步改进

非蒋炎岩老师提及内容
对FORD-FULKERSON算法进行了改进
提出了Boykov-Kolmogorov算法，提高求解速度，求解问题的本质没有变化
Yuri Boykov and Vladimir Kolmogorov An Experimental Comparison of Min-Cut/Max-Flow Algorithms for Energy Minimization in Vision：
https://www.csd.uwo.ca/~yboykov/Papers/pami04.pdf
回到正题
这个算法的重点：就是纠正过去的错误
在这里插入图片描述

在这里插入图片描述

路径寻找与反向边

左图：
错误的走法与正确的走法实质上只是差了那条被多次走过的边，因此只要调整这些反向边就可以了。
右图：
第一步：任意找到一条路径 L1 ，并将这条路径的边调整为反向边;
第二步：在原图的基础上，再找一条路径L2，并将这条路径的边调整为反向边;
…………
…………
直到DFS/BFS 算法终止
DFS/BFS算法会终止，是因为图中出现了大小为0的割。
在这里插入图片描述
将左下的图和右下的图进行对比，方向相悖的边就是我们要找的路径

小结

增广路径
在这里插入图片描述
残留网络

残差网络的例子

problem：已经找到三条路径P1,P2,P3，尝试再找到一条路径
在这里插入图片描述

在这里插入图片描述
当算法终止时，右图为残留网络
蓝色边为原来的边
绿色边是我们处理过的边
利用之前的假设，我们可以反证法证明，
当不存在s–>t的路径时，残差网络的割为0，原网络的割恰好为路径数，因为从T出发，到达S的边不可能穿过两次，穿过两次就会出现矛盾！！
在这里插入图片描述

在这里插入图片描述
因为割的大小决定了路径的上界，而实际上限制路径数的上界的关键，是所有的割中最小的那个割！
也就是说，我们求得的最小的那个割，实际上就是我们可以找到的最大的路径数

小结

目前我们就得到了***最小割和最大流定理的离散版本***

正式谈最大流最小割算法

问题引导

在这里插入图片描述
求解这样的问题，你可以得到一个带权重的有向图，本部分over，非蒋老师的课件内容

带权重的图与不带权重的图的转化

原图
在这里插入图片描述
可以在原图中允许两个点之间存在同向边，这样就可以理解为，权值为多大，边就有多少条。然后使用之前的算法求解，可以证明，这种情况下，算法仍然有效。

也可以直接求解x

引入之前的《算法导论》中的流的概念：
这里将权值视作路径上的容量，不允许有超过容量的路径存在
$x_1:表示s->a->b->t的路径数\\ x_2:表示s->a->b->c->d->t的路径数\\ ………………$
对于权重的约束条件，应满足：
$对边s->a来说，应满足：\\ x_1+x_2+x_3+x_4+…………<=20$
同时我们也得到我们要求解问题的最优表达式：
$\space{ }x_1+x_2+x_3+………………+x_p$
在这里插入图片描述
这样我们就得到了网络流问题的原始表达的线性规划问题
但是这样的线性规划的问题，如果使用一般的方法去求解，计算量巨大，十分不现实，所以，可以这样理解：
通过对这样的线性规划问题的图化，使得将它转化为图论问题，然后利用FORD-FULKERSON算法和Boykov-Kolmogorov算法求解，大大降低算法求解难度；
在这里插入图片描述

关于网络流的定义

在这里插入图片描述
对每条边的权重，认为是它的流量
概括起来就是，除了源点S和汇点T外，流入必定等于流出
可以证明：在满足约束条件的前提下，从s流出的流量一定全部流入t
所以为了求得最大流，只要最大化流出S的流：
所以我们可以得到更加简洁的线性规划表达式，从而降低复杂度.
在这里插入图片描述
最后简要提及了最大流问题和最小割问题的等价性
这里叙述的不是很清楚，建议直接查找《运筹学》的对偶理论。

结尾

好了，蒋炎岩老师用了将近1个小时为你打开了最大流最小割算法的冰山一角，最后推荐了一本参考资料Jeff Erickson:《Algorithms》(可以下载pdf版本)
在此送上链接：
http://jeffe.cs.illinois.edu/teaching/algorithms/
在这里插入图片描述

番外

求解最大流最小割问题，在python语言里并不是难事，因为你总是可以

pip install PyMaxflow

然后接着

import maxflow

一个简单的例子：

import maxflow

# Create a graph with integer capacities.
g = maxflow.Graph[int](2, 2)
# Add two (non-terminal) nodes. Get the index to the first one.
nodes = g.add_nodes(2)
# Create two edges (forwards and backwards) with the given capacities.
# The indices of the nodes are always consecutive.
g.add_edge(nodes[0], nodes[1], 1, 2)
# Set the capacities of the terminal edges...
# ...for the first node.
g.add_tedge(nodes[0], 2, 5)
# ...for the second node.
g.add_tedge(nodes[1], 9, 4)