排序算法

一.冒泡排序
思想：从数组的第一个元素开始，如果后一个元素比当前元素小，那么当前
元素往后走，一直重复的遍历这个数组，直至比较完成
时间复杂度：O(n^2)
有序：1 2 3 4 5 6 O(n)
无序：2 3 6 4 7 5
空间复杂度：O(1)
稳定性：稳定排序(相同数据排序前后是一样的，没有发生跳跃式变化)
核心代码：

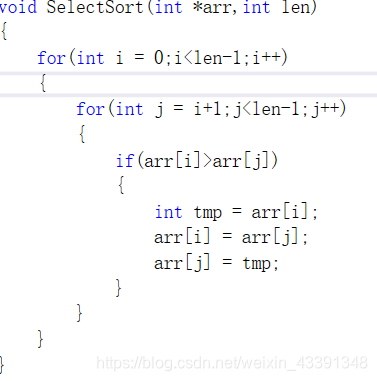
二.选择排序
思想：从待排序数字后找到比待排序数字小的数字就发生交换，直到整个序列遍历完
时间复杂度：O(n^2)
有序：O(n^2)
无序：O(n^2)
空间复杂度：O(1)
稳定性：不稳定
核心代码：

三.直接插入排序
思想：如果有如下一组数字：4,2,6,5,3 首先当我们在最开始的时候，4 是
有序的，然后当拿到数据 2 时，我们需要把 2 放到 4 之前，那也就是
说，我们需要让 4 往后移，然后插入 2，以此类推，我们每次在移动
的时候，是比较一个数字，移动一个数字，并且是从后往前移动
时间复杂度：O(n^2)
有序：O(n) 越有序越快
无序：O(n^2)
空间复杂度：O(1)
稳定性：稳定排序
核心代码：

四.shell（希尔）排序：
分组的思想，组内进行直接插入排序
时间复杂度：O(n^2)
空间复杂度：O(1)
稳定性：稳定性
核心代码：

五.快速排序
思想：找出一个元素作为基准(par),然后对数组进行分区操作,使基准左边元素的值都不大于基准值,基准右边的元素值 都不小于基准值，如此作为基准的元素调整到排序后
的正确位置。递归快速排序，将其他 n-1 个元素也调整到排序后的正确位置。最后每个元素都是在排序后的正 确位置，排序完成。
时间复杂度：O(nlog2n)
空间复杂度：O(log2n)
假设有如下一组数据需要排序：20,3,5,0,32,22,11,8,7,9.我们需要定义
两个变量，intlow,inthigh.分别指向第一个元素和最后一个元素。再
需要一个临时变量，保存每趟的基准值。
时间复杂度：O(nlog2n)
空间复杂度：O(log2n)
稳定性：不稳定
递归主要原代码：
int Partion(int *arr,int low,int high)
{
int tmp = arr[low];
while(low<high)
{
while(low<high&&arr[high]>tmp)
{
high–;
}
if(low>=high)
{
break;
}
else
{
arr[low ]= arr[high];
}
while(low<high&&arr[low]<tmp)
{
low++;
}
if(low>=high)
{
break;
}
else
{
arr[high] = arr[low];
}
}
arr[low] = tmp;
//arr[high] = tmp;
return low;
}
void Quick(int *arr,int start,int end)
{
int par = Partion(arr,start,end);
if(par > start+1)
{
Quick(arr,start,start+1);
}
if(par < end-1 )
{
Quick(arr,end-1,end);
}
}
void QuickSort1(int *arr,int len)
{
Quick(arr,0,len-1);
}
六.堆排序
堆是一棵顺序存储的完全二叉树。
大根堆：父大于子
小根堆：子大于父

思想：将待排序的数组构成一个大根堆，此时整个数组的最大值就是堆结构的顶端
将顶端的数与末尾的数交换，此时末尾的数为最大值，剩余待排序数组个数n-1
将剩余的n-1个数再构成大根堆，再将顶端数与n-1位置的数交换，如此反复执行。
时间复杂度：O(nlog2n)
空间复杂度：O(1)
稳定性：不稳定
主要源代码：
void Adjust(int arr,int start,int end)
{
int tmp = arr[start];
for(int i = 2start+1;i<=end;i=2*i+1)
{
if(i<end&&arr[i]<arr[i+1])
{
i++;
}
if(arr[i]>tmp)
{
arr[start] = arr[i];
start = i;
}
else
{
break;
}
arr[start] = tmp;
}
}
void HeapSort(int *arr,int len)
{
int i = 0;
for(i = (len-1-1)/2;i>=0;i–)
{
Adjust(arr,i,len-1);
}
for(i = 0;i<len-1;i++)
{
int tmp = arr[0];
arr[0] = arr[len-1-i];
arr[len-1-i] = tmp;
Adjust(arr,0,len-1-i-1);
}
}
七、归并排序
即先使每个子序列有序，再使子序列段间有序。
若将两个有序表合并成一个有序表，称为二路归并。

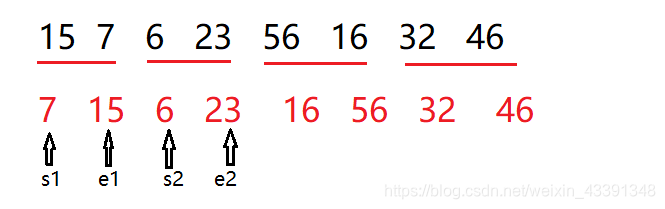
在上图中的， s1,e1,s2,e2 均代表每一个归并段的起始和结尾。
二路归并，一个一个有序归并为两个两个有序。
时间复杂度:O(nlog2n)
空间复杂度：O(n)
稳定性：稳定
主要源代码：
void Merge(int *arr,int len,int gap)//每组有序
{
int *brr = (int *)malloc(sizeof(int) * len);//动态申请内存空间用来保存排好序的数组
assert(brr != NULL);
int i = 0;//brr的下标
int start1 = 0;
int end1 = start1+gap-1;
int start2 = end1+1;
int end2 = start2+gap-1 < len-1 ? start2+gap-1 : len-1;
while(start2 < len) //当有两个归并段的时候
{
while(start1 <= end1 && start2<=end2) //当两个归并段还没有比较完的时候
{
if(arr[start1] <= arr[start2])
{
brr[i++] = arr[start1++];
}
else
{
brr[i++] = arr[start2++];
}
}
while(start1 <= end1)
{
brr[i++] = arr[start1++];
}
while(start2 <= end2)
{
brr[i++] = arr[start2++];
}
start1 = end2+1;//找两个新的归并段
end1 = start1+gap-1;
start2 = end1+1;
end2 = start2+gap-1 < len-1?start2+gap-1:len-1;
}
while(start1 < len)//只有一个归并段的时候
{
brr[i++] = arr[start1++];
}
for(int i = 0;i < len;i++)
{
arr[i] = brr[i];
}
12345678910111213141516171819202122232425262728293031323334353637383940414243
void MergeSort(int *arr,int len)//二路归并排序
{
for(int i = 1;i < len;i *= 2)
{
Merge(arr,len,i);
}
}
八、基数排序
基数排序又称“桶子法”排序，就是有是个桶，序号为0-9，一组待排序数组，先是按个位数字入桶，个位为几就入几号桶，全部入完桶之后从0号桶依次出桶，在桶底的先出桶；
后面是十位，百位数字也用同样的方法入桶。
时间复杂度：O(d(r+n));
空间复杂度：O(rd+n);
稳定性：稳定

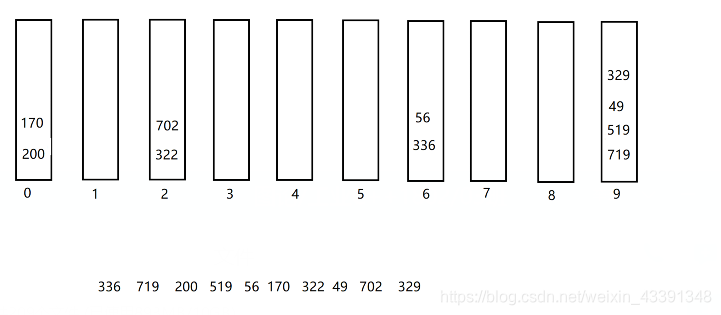
主要源代码：
typedef struct Node
{
int data;
struct Node *next;
}Node,*List;

void InitList(List plist)
{
assert(plist != NULL);
plist->next = NULL;
}
static Node* GetNode(int val)
{
Node pGet = (Node)malloc(sizeof(Node));
assert(pGet != NULL);
pGet->data = val;
pGet->next = NULL;
return pGet;
}
bool Insert(List plist,int val)
{
Node *p = plist;
while(p->next != NULL)
{
p = p->next;
}
Node *pGet = GetNode(val);
p->next = pGet;
return true;
}
bool DeleteFirst(List plist,int *rtv)
{
Node *pDel = plist->next;
if(pDel == NULL)
{
return false;
}
*rtv = pDel->data;
plist->next = pDel->next;
free(pDel);
pDel = NULL;
return true;
}
//123 === > 3位数 n 123/10 12/10 = 1 1/10 = 0
int GetMaxBit(int *arr,int len)
{
//1、你要找到数组的最大值
int max = arr[0];
for(int i = 1;i < len;i++)
{
if(arr[i] > max)
{
max = arr[i];
}
}
//2、算出最大值的位数
int count = 0;
while(max != 0)//123
{
count++;//1 2 3
max /= 10;//12 1 0
}
return count;
}
//123—> 123%10 123/10%10==2 123/10/10%10–>1
int GetNum(int num,int figures)
{
for(int i =0;i < figures;i++)
{
num /= 10;
}
return num % 10;
}
//figures–>从右往左数第figures位的数字 0 ==》 个位
void Radix(int arr,int len,int figures)
{
Node head[10];//
for(int i = 0;i < 10;i++)
{
InitList(&head[i]);
}
//1、入桶–》拿到数字判断第figures位为数字多少，
//入相应的桶里
int tmp = 0;
int i = 0;
for( ; i < len;i++)
{
tmp = GetNum(arr[i],figures);
Insert(&head[tmp],arr[i]);
}
//2、出桶
i = 0;
for(int j = 0;j < 10;)//j代表桶的个数，下标
{
if(DeleteFirst(&head[j],&arr[i]))
{
i++;
}
else
{
j++;
}
}
}
//O(dn)
void RadixSort(int *arr,int len)
{
int count = GetMaxBit(arr,len);
for(int i = 0;i < count;i++)//d
{
Radix(arr,len,i);//n
}
}

void Show(int *arr,int len)
{
for(int i = 0;i < len;i++)
{
printf("%d “,arr[i]);
}
printf(”\n");
}
int main()
{
int arr[] = {12,88,3333,999,4343,223,212,7676,343};
int len = sizeof(arr)/sizeof(arr[0]);
RadixSort(arr,len);
Show(arr,len);
return 0;
}