1.SVM概念
支持向量机即 Support Vector Machine,简称 SVM 。SVM模型的主要思想是在样本特征空间上找到最佳的分离超平面(二维是线)使得训练集上正负样本间隔最大,这个约束使得在感知机的基础上保证可以找到一个最好的分割分离超平面(也就是说感知机会有多个解)。SVM是用来解决二分类问题的有监督学习算法,在引入了核方法之后SVM也可以用来解决非线性问题。
一般SVM有下面三种:
一、线性可分支持向量机
硬间隔支持向量机:硬间隔最大化(hard margin maximization),当训练数据线性可分时,可通过硬间隔最大化学得一个线性可分支持向量机。说的白话一点就是两团数据分的很开,没有你中有我我中有你的情况,画一条线完全可以将数据分开,在数据点不多的情况下我们可以直接通过解析解求得w和b。
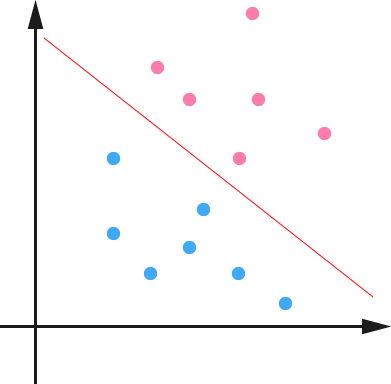
[图1]
二、线性支持向量机
软间隔支持向量机:软间隔最大化(soft margin maximization ),当训练数据近似线性可分时,可通过软间隔最大化学得一个线性支持向量机。两团数据分的很开,存在少量样本点轻微越界的情况,我们可以容忍少部分样本分错,保证得到的模型鲁棒性最高,泛化能力更强。
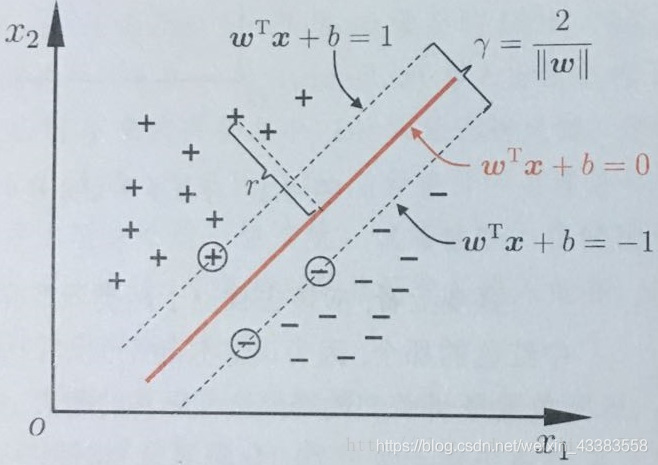
[图2]
三、非线性支持向量机
当训练数据线性不可分时,可通过核方法以及软间隔最大化学得一个非线性支持向量机。
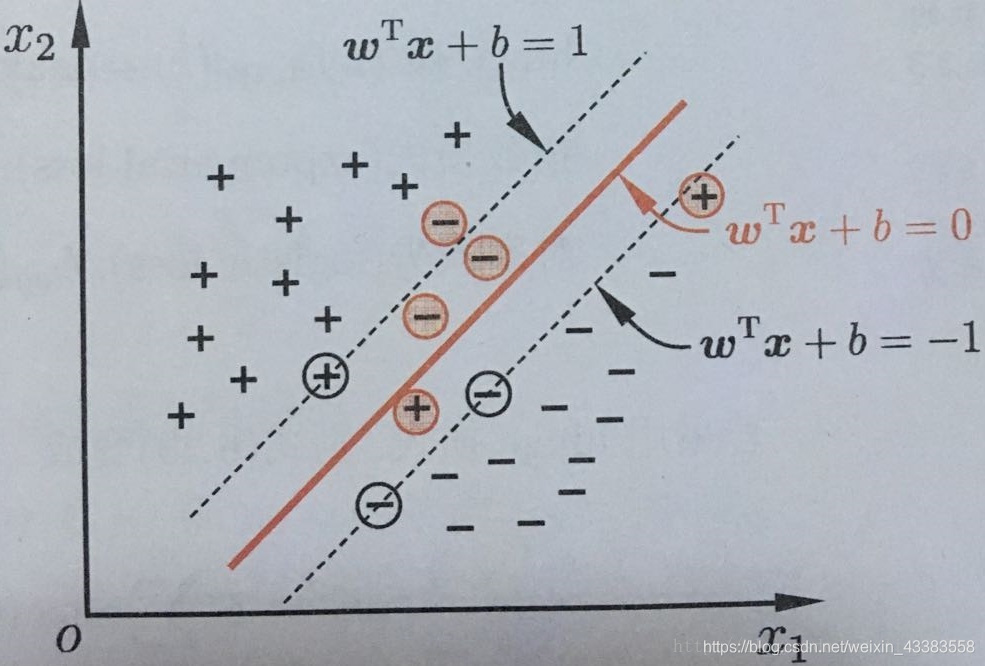
[图3]
SVM 一直被认为是效果最好的现成可用的分类算法之一,即使是现在也常应用在图像识别、文本识别、生物科学和其他科学领域,在金融量化分类中一直是较为理想的,稳定的分类模型。“现成可用”其实是很重要的,因为一直以来学术界和工业界甚至只是学术界里做理论的和做应用的之间,都有一种“鸿沟”,有些很精妙或者很复杂的算法,在抽象出来的模型里很完美,然而在实际问题上却显得很脆弱,效果很差甚至全军覆没。而 SVM 则非常稳定,理论严谨,可以线性分类,也可以高维度非线性分类,工业应用稳定可靠。
2.线性可分支持向量机
给定训练样本集 D = { ( x 1 ⃗ , y 1 ) , ( x 2 ⃗ , y 2 ) , … , ( x n ⃗ , y n ) } , y i ∈ { + 1 , − 1 } D=\{(\vec{x_1},y_1),(\vec{x_2},y_2),\dots,(\vec{x_n},y_n)\},y_i\in\{+1,-1\} D={(x1,y1),(x2,y2),…,(xn,yn)},yi∈{+1,−1}, i i i表示第 i i i个样本, n n n表示样本容量。分类学习最基本的想法就是基于训练集 D D D在特征空间中找到一个最佳划分超平面将正负样本分开,而SVM算法解决的就是如何找到最佳超平面的问题。超平面可通过如下的线性方程来描述:
w ⃗ T x ⃗ + b = 0 \vec{w}^T\vec{x}+b=0 wTx+b=0
其中 w ⃗ T \vec{w}^T wT 表示法向量,决定了超平面的方向; b b b表示偏移量,决定了超平面与原点之间的距离。 对于训练数据集 D D D假设找到了最佳超平面 w ∗ ⃗ x ⃗ + b ∗ = 0 \vec{w^*}\vec{x}+b^*=0 w∗x+b∗=0,定义决策分类函数:
f ( x ⃗ ) = s i g n ( w ∗ ⃗ x ⃗ + b ∗ ) f(\vec{x})=sign(\vec{w^*}\vec{x}+b^*) f(x)=sign(w∗x+b∗)
该分类决策函数也称为线性可分支持向量机,其中
w
∗
⃗
\vec{w^*}
w∗及
b
∗
b^*
b∗为最佳分割超平面所对应的参数,
s
i
g
n
sign
sign是取符号的意思,所以SVM模型只输出正负符号,我们在sklearn等包中的概率等是根据其他算法估算出来的,不是来自SVM算法本身。
在测试时对于线性可分支持向量机可以用一个样本离划分超平面的距离来表示分类预测的可靠程度,如果样本离划分超平面越远则对该样本的分类越可靠,反之就不那么可靠。

[图2],没错还是图2…
空间中超平面可记为
(
w
⃗
,
b
)
(\vec{w},b)
(w,b),根据点到平面的距离公式,空间中任意点
x
⃗
\vec{x}
x 到超平面
(
w
⃗
,
b
)
(\vec{w},b)
(w,b)的距离可写为:
r = w ⃗ x ⃗ + b ∣ ∣ w ⃗ ∣ ∣ r=\frac{\vec{w}\vec{x}+b}{||\vec{w}||} r=∣∣w∣∣wx+b
假设超平面 ( w ⃗ , b ) (\vec{w},b) (w,b)能将训练样本正确分类,那么对于正样本一侧的任意一个样本 ( x i ⃗ , y i ) ∈ D (\vec{x_i},y_i)\in{D} (xi,yi)∈D,应该需要满足该样本点 x ⃗ \vec{x} x到超平面的法向量 w ∗ ⃗ \vec{w^*} w∗的投影到原点的距离大于一定值 c c c的时候使得该样本点被预测为正样本一类,即存在数值 c c c使得当 w ⃗ T x i ⃗ > c \vec{w}^T\vec{x_i}>c wTxi>c, y i = + 1 y_i=+1 yi=+1。 w ⃗ T x i ⃗ > c \vec{w}^T\vec{x_i}>c wTxi>c又可写为 w ⃗ T x i ⃗ + b > 0 \vec{w}^T\vec{x_i}+b>0 wTxi+b>0。在训练的时候我们要求限制条件更严格点以使最终得到的分类器鲁棒性更强,所以我们要求 w ⃗ T x i ⃗ + b > 1 \vec{w}^T\vec{x_i}+b>1 wTxi+b>1。也可以写为大于其它距离,但都可以通过同比例缩放 w ⃗ \vec{w} w和 b b b来使得使其变为1,因此为计算方便这里直接选择1。同样对于负样本应该有 w ⃗ T x i ⃗ + b < − 1 \vec{w}^T\vec{x_i}+b<-1 wTxi+b<−1时 y i = − 1 y_i=-1 yi=−1。即:
{ w ⃗ T x i ⃗ + b ≥ + 1 , y i = + 1 w ⃗ T x i ⃗ + b ≤ − 1 , y i = − 1 \begin{cases} \vec{w}^T\vec{x_i}+b\geq+1, & y_i=+1 \\ \vec{w}^T\vec{x_i}+b\leq-1, & y_i=-1 \end{cases} {wTxi+b≥+1,wTxi+b≤−1,yi=+1yi=−1
亦即:
y i ( w ⃗ T x i ⃗ + b ) ≥ + 1 y_i(\vec{w}^T\vec{x_i}+b)\geq+1 yi(wTxi+b)≥+1
如图2所示,距离最佳超平面 w ⃗ x ⃗ + b = 0 \vec{w}\vec{x}+b=0 wx+b=0最近的几个训练样本点使上式中的等号成立,它们被称为“支持向量”(support vector)。记超平面 w ⃗ x ⃗ + b = + 1 \vec{w}\vec{x}+b=+1 wx+b=+1和 w ⃗ x ⃗ + b = − 1 \vec{w}\vec{x}+b=-1 wx+b=−1之间的距离为 γ γ γ,该距离又被称为“间隔”(margin),SVM的核心之一就是想办法将“间隔” γ γ γ最大化。下面我们推导一下 γ γ γ与哪些因素有关:
我们初中就已经学过了两条平行线间距离的求法,例如 a x + b y = c 1 ax+by=c1 ax+by=c1和 a x + b y = c 2 ax+by=c2 ax+by=c2,那他们的距离是 ∣ c 2 − c 1 ∣ ( a 2 + b 2 ) \frac{|c2-c1|}{\sqrt{(a^2+b^2)}} (a2+b2)∣c2−c1∣。注意的是,这里的x和y都表示二维坐标(即代表特征里的x1及x2)。而用w来表示就是 H 1 : w 1 x 1 + w 2 x 2 = + 1 H1:w_1x_1+w_2x_2=+1 H1:w1x1+w2x2=+1和 H 2 : w 1 x 1 + w 2 x 2 = − 1 H2:w_1x_1+w_2x_2=-1 H2:w1x1+w2x2=−1,那H1和H2的距离就是 ∣ 1 + 1 ∣ ( w 1 2 + w 2 2 ) = 2 ∣ ∣ w ∣ ∣ \frac{|1+1|}{\sqrt{(w_1^2+w_2^2)}}=\frac{2}{||w||} (w12+w22)∣1+1∣=∣∣w∣∣2。也就是w的模的倒数的两倍。也就是说,我们需要最大化 γ \gamma γ:
γ = 2 ∣ ∣ w ⃗ ∣ ∣ \gamma=\frac{2}{||\vec{w}||} γ=∣∣w∣∣2
也就是说使两类样本距离最大的因素仅仅和最佳超平面的法向量(系数w)有关。 要找到具有“最大间隔”(maximum margin)的最佳超平面,就是找到能满约束的参数 w ⃗ \vec{w} w、 b b b使得 γ γ γ最大,即:
{ max w ⃗ , b 2 ∣ ∣ w ⃗ ∣ ∣ s . t . y i ( w ⃗ T x i ⃗ + b ) ≥ + 1 , i = 1 , 2 , … , n \begin{cases} \max_{\vec{w},b}\frac{2}{||\vec{w}||} \\ s.t.\quad y_i(\vec{w}^T\vec{x_i}+b)\geq+1, i=1,2,\dots,n \end{cases} {maxw,b∣∣w∣∣2s.t.yi(wTxi+b)≥+1,i=1,2,…,n
最大化这个距离等价于最小化 ∣ ∣ w ⃗ ∣ ∣ ||\vec{w}|| ∣∣w∣∣,我们给最小化公式来个平方,乘以1/2都是等价的:
{ min w ⃗ , b 1 2 ∣ ∣ w ⃗ ∣ ∣ 2 s . t . y i ( w ⃗ T x i ⃗ + b ) ≥ + 1 , i = 1 , 2 , … , n \begin{cases} \min_{\vec{w},b}\frac{1}{2}||\vec{w}||^2 \\ s.t.\quad y_i(\vec{w}^T\vec{x_i}+b)\geq+1, i=1,2,\dots,n \end{cases} {minw,b21∣∣w∣∣2s.t.yi(wTxi+b)≥+1,i=1,2,…,n
2.1使用最优化包直接求解w和b
那么问题来了,怎么求这个 min 1 2 ∣ ∣ w ⃗ ∣ ∣ 2 \min\frac{1}{2}||\vec{w}||^2 min21∣∣w∣∣2公式的最小化呢?先来个简单粗暴的方法,针对数据点较少的情况,我们用最优化包scipy.optimize.fmin_l_bfgs_b直接求解(代码参考来源:余凯_西二旗民工):
# 定义目标函数,w是未知数据,args是已知数,求w的最优解
def func(w,*args):
X,Y,c=args
yp=np.dot(X,w) # w*x,注意已经将b作为x的第一列进行了计算,w*x就是我们现在预测的y
idx=np.where(yp*Y<1)[0] # 找到分错的数据索引位置
e=yp[idx]-Y[idx] # y预测值-y真实值,误差
cost=np.dot(e,e)+c*np.dot(w,w) # 平方和损失,c:学习率,加w的二范式惩罚
grand=2*(np.dot(X[idx].T,e)+c*w)# 梯度下降??
return cost,grand
if __name__ == '__main__':
##1、SVM直接求参数值#############################################################
print('\n1、SVM直接求参数值,开始')
# 生成数据,《统计学习方法》李航,P103,例7.1
dataSet=np.array([[3,3,1],[4,3,1],[1,1,-1]]) # ,[0,0,-1],[0,1,-1]
m, n = dataSet.shape
x=dataSet[:,:-1]
y=dataSet[:,-1] #.reshape((-1,1))
# 数据定义
X=np.append(np.ones([x.shape[0],1]),x,1) # x新增一列全1值,作为截距b
Y=y
c=0.001 # 学习率
w=np.zeros(X.shape[1]) # 初始化一组w系数,全0,也可随机产生:np.random.rand(X.shape[1])
# bfgs_b方法求最优化问题
REF=fmin_l_bfgs_b(func,x0=w,args=(X,Y,c),approx_grad=False) #x0=np.random.rand(X.shape[1]) [0,0,0]
# 采用scipy.optimize其他包夜可以求得
REF2=fmin_tnc(func,x0=w,args=(X,Y,c),approx_grad=False)
# 求得最优化计算后的w
w=REF[0].round(2) # 取得w值
print('w:',w[1:],'b:',w[0]) # 与《统计学习方法》李航,P103,例7.1计算结果一致
# 画图
plotResult(w)
print('\n1、SVM直接求参数值,结束')
来看看求解结果,貌似还不错基本接近李航老师的结果(结果进行了四舍五入):
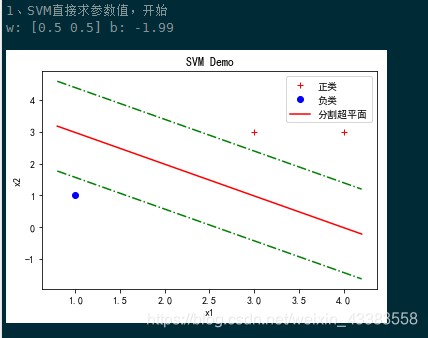
[图4]
2.2使用Dual优化
2.1节中直接使用最优化包求解可能并不高效,迭代过程也不可见,我们可以将该凸二次规划问题通过拉格朗日对偶性来求解。
对于上式
min
1
2
∣
∣
w
⃗
∣
∣
2
\min\frac{1}{2}||\vec{w}||^2
min21∣∣w∣∣2,我们引入带约束的拉格朗日乘子
α
i
≥
0
α_i≥0
αi≥0,得到拉格朗日函数:
L ( w ⃗ , b , α ⃗ ) = 1 2 ∣ ∣ w ⃗ ∣ ∣ 2 − ∑ i = 1 n α i ( y i ( w ⃗ T x i + b ) − 1 ) L(\vec{w},b,\vec{\alpha})=\frac{1}{2}||\vec{w}||^2-\sum_{i=1}^{n}{\alpha_i(y_i(\vec{w}^Tx_i+b)-1)} L(w,b,α)=21∣∣w∣∣2−∑i=1nαi(yi(wTxi+b)−1)
需要注意公式后半部分求和,它指的是我们有m行数据,就会有m个 α i \alpha_i αi,个人理解分错的数据 ( x i ⃗ , y i ) (\vec{x_i},y_i) (xi,yi), α i ( y i ( w ⃗ T x i + b ) − 1 ) {\alpha_i(y_i(\vec{w}^Tx_i+b)-1)} αi(yi(wTxi+b)−1)值不接近0,分对的数据此项值无限接近0,相当于变相求误差。
对上式 L ( w ⃗ , b , α ⃗ ) L(\vec{w},b,\vec{\alpha}) L(w,b,α)分别对 w ⃗ \vec{w} w和 b b b求极值,也就是 L ( w ⃗ , b , α ⃗ ) L(\vec{w},b,\vec{\alpha}) L(w,b,α)对 w ⃗ \vec{w} w和 b b b的梯度为0: ∂ L / ∂ w = 0 ∂L/∂w=0 ∂L/∂w=0和 ∂ L / ∂ b = 0 ∂L/∂b=0 ∂L/∂b=0,还需要满足 α > = 0 α>=0 α>=0。求解这里导数为0的式子可以得到:
{ w ⃗ = ∑ i = 1 n α i y i x i ⃗ ∑ i = 1 n α i y i = 0 \begin{cases} \vec{w}=\sum_{i=1}^{n}{\alpha_iy_i\vec{x_i}}\\ \sum_{i=1}^{n}{\alpha_iy_i}=0 \end{cases} {w=∑i=1nαiyixi∑i=1nαiyi=0
有没有发现上式非常惊艳,求得 α α α后,带一下公式 w ⃗ \vec{w} w就求出来了!将上式带入 L ( w ⃗ , b , α ⃗ ) L(\vec{w},b,\vec{\alpha}) L(w,b,α)函数替换掉 w ⃗ \vec{w} w和 b b b,得到以下结果:
{ max . W ( α ) = ∑ i = 1 n α i − 1 2 ∑ i = 1 n ∑ j = 1 n α i α j y i y j x i ⃗ T x j ⃗ s . t . α i ≥ 0 , i = 1 , 2 , … , n ∑ i = 1 n α i y i = 0 \begin{cases} \max._W(\alpha)={\sum_{i=1}^{n}\alpha_i-\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha_i\alpha_jy_iy_j\vec{x_i}^T\vec{x_j}}\\ s.t.\quad \alpha_i\geq0,i=1,2,\dots,n \\ \quad\quad\quad \sum_{i=1}^{n}\alpha_iy_i=0 \end{cases} ⎩⎪⎨⎪⎧max.W(α)=∑i=1nαi−21∑i=1n∑j=1nαiαjyiyjxiTxjs.t.αi≥0,i=1,2,…,n∑i=1nαiyi=0
这个就是dual problem(如果我们知道 α α α,我们就知道了 w w w。反过来,如果我们知道w,也可以知道 α α α)。这时候我们就变成了求对 α α α的极大,即是关于对偶变量 α α α的优化问题(没有了变量 w , b w,b w,b,只有 α α α)。当求解得到最优的 α ∗ α^* α∗后,就可以同样代入到上面的公式,导出 w ∗ w^* w∗和 b ∗ b^* b∗了,最终得出分离超平面和分类决策函数。也就是训练好了SVM。那来一个新的样本 x x x后,就可以这样分类了:
f
(
x
⃗
)
=
s
i
g
n
(
w
⃗
T
x
⃗
+
b
)
f(\vec{x})=sign(\vec{w}^T\vec{x}+b)
f(x)=sign(wTx+b)
=
s
i
g
n
(
(
∑
i
=
1
n
α
i
y
i
x
i
⃗
)
∗
x
+
b
)
=sign((\sum_{i=1}^{n}{\alpha_iy_i\vec{x_i}})*x+b)
=sign((∑i=1nαiyixi)∗x+b)
=
s
i
g
n
(
∑
i
=
1
n
α
i
y
i
(
x
i
⃗
∗
x
)
+
b
)
=sign(\sum_{i=1}^{n}{\alpha_iy_i}(\vec{x_i}*x)+b)
=sign(∑i=1nαiyi(xi∗x)+b)
在这里,其实很多的 α i α_i αi都是0,也就是说w只是一些少量样本的线性加权值。这种“稀疏”的表示实际上看成是KNN的数据压缩的版本。也就是说,以后新来的要分类的样本首先根据 w w w和 b b b做一次线性运算,然后看求的结果是大于0还是小于0来判断正例还是负例。现在有了 α i α_i αi,我们不需要求出 w w w,只需将新来的样本和训练数据中的所有样本做内积和即可。那有人会说,与前面所有的样本都做运算是不是太耗时了?其实不然,我们从KKT条件中得到,只有支持向量的 α i α_i αi不为0,其他情况 α i α_i αi都是0。因此,我们只需求新来的样本和支持向量的内积,然后运算即可。这种写法为下面要提到的核函数(kernel)(就是将 x i ⃗ ∗ x \vec{x_i}*x xi∗x引入核函数)做了很好的铺垫。
2.3Python实现smoSimple核心代码
# 输入变量:x、y、c:常数c、toler:容错率、maxIter:最大循环次数
def smoSimple(dataMatIn, classLabels, C, toler, maxIter):
#dataMatIn, classLabels, C, toler, maxIter=dataArr,lableArr,0.6,0.001,40
dataMatrix = np.mat(dataMatIn) # 数据x转换为matrix类型
labelMat = np.mat(classLabels).transpose() # 标签y转换为matrix类型,转换为一列
b = 0 # 截距b
m,n = np.shape(dataMatrix) # 数据x行数、列数
alphas = np.mat(np.zeros((m,1))) # 初始化alpha,有多少行数据就产生多少个alpha
iter = 0 # 遍历计数器
while (iter < maxIter):
#print( "iteration number: %d" % iter)
alphaPairsChanged = 0 # 记录alpha是否已被优化,每次循环都重置
for i in range(m): # 按行遍历数据,类似随机梯度下降
# i=0
fXi = float(np.multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[i,:].T)) + b # 预测值y,g(x)函数,《统计学习方法》李航P127,7.104
Ei = fXi - float(labelMat[i])#if checks if an example violates KKT conditions # 误差,Ei函数,P127,7.105
if ((labelMat[i]*Ei < -toler) and (alphas[i] < C)) or ((labelMat[i]*Ei > toler) and (alphas[i] > 0)):
# 找第一个alphas[i],找到第一个满足判断条件的,判断负间隔or正间隔,并且保证0<alphas<C
j = selectJrand(i,m) # 随机找到第二个alphas[j]
fXj = float(np.multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[j,:].T)) + b # 计算预测值
Ej = fXj - float(labelMat[j]) # 计算alphas[j]误差
alphaIold = alphas[i].copy() # 记录上一次alphas[i]值
alphaJold = alphas[j].copy() # 记录上一次alphas[j]值
if (labelMat[i] != labelMat[j]):# 计算H及L值,《统计学习方法》李航,P126
L = max(0, alphas[j] - alphas[i])
H = min(C, C + alphas[j] - alphas[i])
else:
L = max(0, alphas[j] + alphas[i] - C)
H = min(C, alphas[j] + alphas[i])
if L==H:
#print( "L==H")
continue
eta = 2.0 * dataMatrix[i,:]*dataMatrix[j,:].T - dataMatrix[i,:]*dataMatrix[i,:].T - dataMatrix[j,:]*dataMatrix[j,:].T
# 《统计学习方法》李航P127,7.107,这里的eta与李航的一致,这里乘了负号
if eta >= 0:
#print("eta>=0")
continue
alphas[j] -= labelMat[j]*(Ei - Ej)/eta # 《统计学习方法》李航P127,7.107,更新alphas[j]
alphas[j] = clipAlpha(alphas[j],H,L) # alphas[j]调整大于H或小于L的alpha值
if (abs(alphas[j] - alphaJold) < 0.00001): # 调整后过小,则不更新alphas[i]
#print( "j not moving enough")
continue
alphas[i] += labelMat[j]*labelMat[i]*(alphaJold - alphas[j]) #更新alphas[i],《统计学习方法》李航P127,7.109
# 更新b值,《统计学习方法》李航P130,7.115,7.116
b1 = b - Ei- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[i,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[i,:]*dataMatrix[j,:].T
b2 = b - Ej- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[j,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[j,:]*dataMatrix[j,:].T
if (0 < alphas[i]) and (C > alphas[i]): # 判断符合条件的b
b = b1
elif (0 < alphas[j]) and (C > alphas[j]):
b = b2
else:
b = (b1 + b2)/2.0
alphaPairsChanged += 1
#print( "iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged))
if (alphaPairsChanged == 0):
iter += 1
else:
iter = 0
return b,alphas
根据alpha求解w, w ⃗ = ∑ i = 1 n α i y i x i ⃗ \vec{w}=\sum_{i=1}^{n}{\alpha_iy_i\vec{x_i}} w=∑i=1nαiyixi:
def calcWs(alphas,dataArr,labelArr):
w=sum( np.array(alphas) * np.array(labelArr.reshape((-1,1))) * np.array(np.array(dataArr)) )
return w
线性可分支持向量机运行结果:
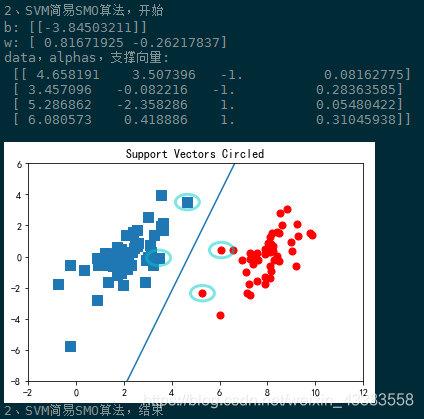
[图5]
3.线性支持向量机
3.1软间隔支持向量机
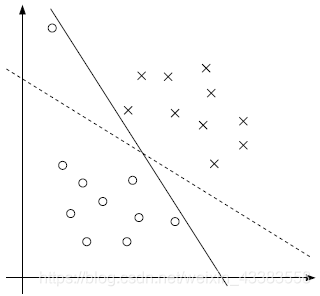
[图6]
如上图,直线是我们学习获得的超平面,但有一个圆点离群了,我们是否应该不考虑这个点,获得新的虚线所示的超平面,这个虚线所示超平面泛化能力比原有超平面要好很多。 依此想法我们引出了软间隔支持向量机,不一定分类完全正确的,超平面就是最好,样本数据身线性不可分的情况也可以使用。软间隔支持向量机容许在一些样本上出错,为此引入了“软间隔”(soft margin)的概念

[图3],没错还是图3…
具体来说,硬间隔支持向量机要求所有的样本均被最佳超平面正确划分,而软间隔支持向量机允许某些样本点不满足间隔大于等于1的条件
y
i
(
w
⃗
x
i
⃗
+
b
)
≥
1
y_i(\vec{w}\vec{x_i}+b)\geq1
yi(wxi+b)≥1,当然在最大化间隔的时候也要限制不满足间隔大于等于1的样本的个数使之尽可能的少。于是我们引入一个惩罚系数
C
>
0
C>0
C>0,并对每个样本点
(
x
i
⃗
,
y
i
)
(\vec{x_i},y_i)
(xi,yi)引入一个松弛变量(slack variables)
ξ
≥
0
ξ≥0
ξ≥0:
{ min w ⃗ , b ( 1 2 ∣ ∣ w ⃗ ∣ ∣ 2 + C ∑ i = 1 n ξ i ) s . t . y i ( w ⃗ T x i ⃗ + b ) ≥ 1 − ξ i , i = 1 , 2 , … , n ξ i ≥ 0 \begin{cases} \min_{\vec{w},b}(\frac{1}{2}||\vec{w}||^2+C\sum_{i=1}^{n}\xi_i) \\ s.t.\quad y_i(\vec{w}^T\vec{x_i}+b)\geq1-\xi_i \quad ,i=1,2,\dots,n\\ \quad\quad \xi_i\geq0 \end{cases} ⎩⎪⎨⎪⎧minw,b(21∣∣w∣∣2+C∑i=1nξi)s.t.yi(wTxi+b)≥1−ξi,i=1,2,…,nξi≥0
利用拉格朗日乘子法可得到上式的拉格朗日函数:
L ( w ⃗ , b , α ⃗ , ξ ⃗ , μ ⃗ ) = 1 2 ∣ ∣ w ⃗ ∣ ∣ 2 + C ∑ i = 1 n ξ i − ∑ i = 1 n α i ( y i ( w ⃗ T x i ⃗ + b ) − 1 + ξ i ) − ∑ i = 1 n μ i ξ i L(\vec{w},b,\vec{\alpha},\vec{\xi},\vec{\mu})=\frac{1}{2}||\vec{w}||^2+C\sum_{i=1}^{n}\xi_i-\sum_{i=1}^{n}\alpha_i(y_i(\vec{w}^T\vec{x_i}+b)-1+\xi_i)-\sum_{i=1}^{n}\mu_i\xi_i L(w,b,α,ξ,μ)=21∣∣w∣∣2+C∑i=1nξi−∑i=1nαi(yi(wTxi+b)−1+ξi)−∑i=1nμiξi
将上式带入 L ( w ⃗ , b , α ⃗ ) L(\vec{w},b,\vec{\alpha}) L(w,b,α)函数替换掉 w ⃗ \vec{w} w和 b b b,得到以下结果:
{ max α ⃗ ∑ i = 1 n α i − 1 2 ∑ i = 1 n ∑ j = 1 n α i α j y i y j x i ⃗ T x j ⃗ s . t . ∑ i = 1 n α i y i = 0 , i = 1 , 2 , … , n 0 ≤ α i ≤ C \begin{cases} \max_{\vec\alpha}\sum_{i=1}^{n}\alpha_i-\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha_i\alpha_jy_iy_j\vec{x_i}^T\vec{x_j}\\ s.t. \quad\quad\sum_{i=1}^{n}\alpha_iy_i=0\quad\quad,i=1,2,\dots,n\\ \quad\quad\quad 0\leq\alpha_i\leq C \end{cases} ⎩⎪⎨⎪⎧maxα∑i=1nαi−21∑i=1n∑j=1nαiαjyiyjxiTxjs.t.∑i=1nαiyi=0,i=1,2,…,n0≤αi≤C
对比软间隔支持向量机的对偶问题和硬间隔支持向量机的对偶问题可发现二者的唯一差别就在于对偶变量的约束不同,软间隔支持向量机对对偶变量的约束是 0 ≤ α i ≤ C 0≤α_i≤C 0≤αi≤C,硬间隔支持向量机对对偶变量的约束是 0 ≤ α i 0≤α_i 0≤αi。
软间隔支持向量机,KKT条件要求:
{
α
i
≥
0
,
μ
i
≥
0
y
i
(
w
⃗
x
⃗
+
b
)
−
1
+
ξ
i
≥
0
α
i
(
y
i
(
w
⃗
x
⃗
+
b
)
−
1
+
ξ
i
)
=
0
ξ
i
≥
0
,
μ
i
ξ
i
=
0
\begin{cases} \alpha_i\geq0,\mu_i\geq0\\ y_i(\vec{w}\vec{x}+b)-1+\xi_i\geq0\\ \alpha_i(y_i(\vec{w}\vec{x}+b)-1+\xi_i)=0\\ \xi_i\geq0,\mu_i\xi_i=0 \end{cases}
⎩⎪⎪⎪⎨⎪⎪⎪⎧αi≥0,μi≥0yi(wx+b)−1+ξi≥0αi(yi(wx+b)−1+ξi)=0ξi≥0,μiξi=0
同硬间隔支持向量机类似,对任意训练样本 ( x i ⃗ , y i ) (\vec{x_i},y_i) (xi,yi),总有 α i = 0 α_i=0 αi=0或 y i ( w ⃗ x ⃗ + b − 1 + ξ i ) y_i(\vec{w}\vec{x}+b-1+\xi_i) yi(wx+b−1+ξi),若αi=0αi=0,则该样本不会对最佳决策面有任何影响;若 α i > 0 α_i>0 αi>0则必有 y i ( w ⃗ x ⃗ + b ) = 1 − ξ i y_i(\vec{w}\vec{x}+b)=1-\xi_i yi(wx+b)=1−ξi,也就是说该样本是支持向量。若 α i < C α_i<C αi<C则 μ i > 0 μ_i>0 μi>0进而有 ξ i = 0 ξ_i=0 ξi=0,即该样本处在最大间隔边界上;若 α i = C α_i=C αi=C则 μ i = 0 μ_i=0 μi=0此时如果 x i i ≤ 1 xi_i≤1 xii≤1则该样本处于最大间隔内部,如果 ξ i > 1 ξ_i>1 ξi>1则该样本处于最大间隔外部即被分错了。由此也可看出,软间隔支持向量机的最终模型仅与支持向量有关。
4.非线性支持向量机
4.1核函数
现实任务中原始的样本空间D中很可能并不存在一个能正确划分两类样本的超平面。工程学中经常会遇到的问题,无法找到一个超平面将两类样本进行很好的划分。 这种情况我们引入核函数( kernel function )来解决,将
(
x
i
⃗
∗
x
)
(\vec{x_i}*x)
(xi∗x)引入核函数。
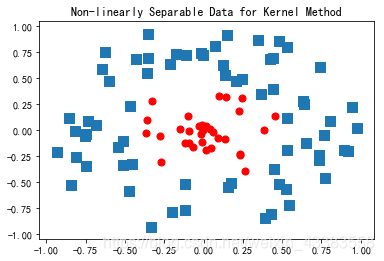
[图7]
令
ϕ
(
x
⃗
)
ϕ(\vec{x} )
ϕ(x)表示将样本点
x
⃗
\vec{x}
x映射后的特征向量,类似于线性可分支持向量机中的表示方法,在特征空间中划分超平面所对应的模型可表示为:
f ( x ⃗ ) = w ⃗ T x + b f(\vec{x})=\vec{w}^Tx+b f(x)=wTx+b
其中 w ⃗ \vec{w} w和 b b b是待求解的模型参数。
{ min w ⃗ , b 1 2 ∣ ∣ w ⃗ ∣ ∣ 2 s . t . y i ( w ⃗ T ϕ ( x ⃗ ) + b ) ≥ 1 , i = 1 , 2 , … , n \begin{cases} \min_{\vec{w},b}\frac{1}{2}||\vec{w}||^2\\ s.t. \quad y_i(\vec{w}^T\phi(\vec{x})+b)\geq1\quad,i=1,2,\dots,n \end{cases} {minw,b21∣∣w∣∣2s.t.yi(wTϕ(x)+b)≥1,i=1,2,…,n
其拉格朗日对偶问题是:
{ max α ∑ i = 1 n α i − 1 2 ∑ i = 1 n ∑ j = 1 n α i α j y i y j ϕ ( x i ⃗ T ) ϕ ( x j ⃗ ) s . t . α i ≥ 0 , i = 1 , 2 , … , n ∑ i = 1 n α i y i = 0 \begin{cases} \max_\alpha{\sum_{i=1}^{n}\alpha_i-\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha_i\alpha_jy_iy_j\phi(\vec{x_i}^T)\phi(\vec{x_j})}\\ s.t.\quad \alpha_i\geq0\quad\quad\quad,i=1,2,\dots,n \\ \quad\quad\quad \sum_{i=1}^{n}\alpha_iy_i=0 \end{cases} ⎩⎪⎨⎪⎧maxα∑i=1nαi−21∑i=1n∑j=1nαiαjyiyjϕ(xiT)ϕ(xj)s.t.αi≥0,i=1,2,…,n∑i=1nαiyi=0
需要计算 ϕ ( x i ⃗ T ) ϕ(\vec{x_i}^T) ϕ(xiT) ϕ ( x j ⃗ ) ϕ(\vec{x_j}) ϕ(xj),即样本映射到特征空间之后的内积,由于特征空间可能维度很高,甚至可能是无穷维,因此直接计算 ϕ ( x i ⃗ T ) ϕ(\vec{x_i}^T) ϕ(xiT) ϕ ( x j ⃗ ) ϕ(\vec{x_j}) ϕ(xj)通常是很困难的,在上文中我们提到其实我们根本不关心单个样本的表现,只关心特征空间中样本间两两的乘积,因此我们没有必要把原始空间的样本一个个地映射到特征空间中,只需要想法办求解出样本对应到特征空间中样本间两两的乘积即可。为了解决该问题可设想存在核函数:
κ ( x i ⃗ , x j ⃗ ) = ϕ ( x i ⃗ T ) ϕ ( x j ⃗ ) \kappa(\vec{x_i},\vec{x_j})=\phi(\vec{x_i}^T)\phi(\vec{x_j}) κ(xi,xj)=ϕ(xiT)ϕ(xj)
也就是说 x i ⃗ \vec{x_i} xi与 x j ⃗ \vec{x_j} xj在特征空间的内积等于它们在原始空间中通过函数κ(⋅,⋅)计算的结果,这给求解带来很大的方便。
{ max α ∑ i = 1 n α i − 1 2 ∑ i = 1 n ∑ j = 1 n α i α j y i y j κ < x i ⃗ , x j ⃗ > s . t . α i ≥ 0 , i = 1 , 2 , … , n ∑ i = 1 n α i y i = 0 \begin{cases} \max_\alpha{\sum_{i=1}^{n}\alpha_i-\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha_i\alpha_jy_iy_j\kappa<\vec{x_i},\vec{x_j}>}\\ s.t.\quad \alpha_i\geq0\quad\quad\quad,i=1,2,\dots,n \\ \quad\quad\quad \sum_{i=1}^{n}\alpha_iy_i=0 \end{cases} ⎩⎪⎨⎪⎧maxα∑i=1nαi−21∑i=1n∑j=1nαiαjyiyjκ<xi,xj>s.t.αi≥0,i=1,2,…,n∑i=1nαiyi=0
同样的我们只关心在高维空间中样本之间两两点乘的结果而不关心样本是如何变换到高维空间中去的。求解后即可得到:
f ( x ⃗ ) = w ⃗ T ϕ ( x ⃗ ) + b = ∑ i = 1 n α i y i ϕ ( x ⃗ ) T ϕ ( x ⃗ ) + b = ∑ i = 1 n α i y i κ < x i ⃗ , x j ⃗ > + b f(\vec{x})=\vec{w}^T\phi(\vec{x})+b=\sum_{i=1}^{n}\alpha_iy_i\phi(\vec{x})^T\phi(\vec{x})+b=\sum_{i=1}^{n}\alpha_iy_i\kappa<\vec{x_i},\vec{x_j}>+b f(x)=wTϕ(x)+b=∑i=1nαiyiϕ(x)Tϕ(x)+b=∑i=1nαiyiκ<xi,xj>+b
剩余的问题同样是求解 α i α_i αi,然后求解 w ⃗ \vec{w} w和 b b b即可得到最佳超平面。
常用的核函数:

[图8]
核函数python实现:
# 核函数
def kernelTrans(X, A, kTup): #calc the kernel or transform data to a higher dimensional space
m,n = np.shape(X)
K = np.mat(np.zeros((m,1)))
if kTup[0]=='lin': K = X * A.T #linear kernel
elif kTup[0]=='rbf':
for j in range(m):
deltaRow = X[j,:] - A
K[j] = deltaRow*deltaRow.T
K = np.exp(K/(-1*kTup[1]**2)) #divide in NumPy is element-wise not matrix like Matlab
else: raise NameError('Houston We Have a Problem -- \
That Kernel is not recognized')
return K
4.2SMO算法
SMO算法的思想和梯度下降法的思想差不多。唯一不同的是,SMO是一次迭代优化两个α而不是一个。为什么要优化两个呢?
SVM的学习问题可以转化为下面的对偶问题:
{ max α ∑ i = 1 n α i − 1 2 ∑ i = 1 n ∑ j = 1 n α i α j y i y j κ < x i ⃗ , x j ⃗ > s . t . α i ≥ 0 , i = 1 , 2 , … , n ∑ i = 1 n α i y i = 0 \begin{cases} \max_\alpha{\sum_{i=1}^{n}\alpha_i-\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha_i\alpha_jy_iy_j\kappa<\vec{x_i},\vec{x_j}>}\\ s.t.\quad \alpha_i\geq0\quad\quad\quad,i=1,2,\dots,n \\ \quad\quad\quad \sum_{i=1}^{n}\alpha_iy_i=0 \end{cases} ⎩⎪⎨⎪⎧maxα∑i=1nαi−21∑i=1n∑j=1nαiαjyiyjκ<xi,xj>s.t.αi≥0,i=1,2,…,n∑i=1nαiyi=0
这个优化问题,我们可以看到这个优化问题存在着一个约束,也就是:
∑ i = 1 n α i y i = 0 \sum_{i=1}^{n}\alpha_iy_i=0 ∑i=1nαiyi=0
假设我们首先固定除 α 1 α_1 α1以外的所有参数,然后在 α 1 α_1 α1上求极值。但需要注意的是,因为如果固定 α 1 α_1 α1以外的所有参数,由上面这个约束条件可以知道, α 1 α_1 α1将不再是变量(可以由其他值推出),因为问题中规定了:
α 1 y ( 1 ) = ∑ i = 2 n α i y i α_1y^{(1)}=\sum_{i=2}^{n}\alpha_iy_i α1y(1)=∑i=2nαiyi
因此,我们需要一次选取两个参数做优化,比如 α i α_i αi和 α j α_j αj,此时 α i α_i αi可以由 α j α_j αj和其他参数表示出来。这样回代入W中,W就只是关于 α j α_j αj的函数了,这时候就可以只对 α j α_j αj进行优化了。在这里就是对 α j α_j αj进行求导,令导数为0就可以解出这个时候最优的 α j α_j αj了。然后也可以得到αi。这就是一次的迭代过程,一次迭代只调整两个拉格朗日乘子 α i α_i αi和 α j α_j αj。SMO之所以高效就是因为在固定其他参数后,对一个参数优化过程很高效(对一个参数的优化可以通过解析求解,而不是迭代。虽然对一个参数的一次最小优化不可能保证其结果就是所优化的拉格朗日乘子的最终结果,但会使目标函数向极小值迈进一步,这样对所有的乘子做最小优化,直到所有满足KKT条件时,目标函数达到最小)。
总结下来是:
重复下面过程直到收敛{
(1)选择两个拉格朗日乘子
α
i
α_i
αi和
α
j
α_j
αj;
(2)固定其他拉格朗日乘子
α
k
α_k
αk(k不等于i和j),只对
α
i
α_i
αi和
α
j
α_j
αj优化
w
(
α
)
w(α)
w(α);
(3)根据优化后的
α
i
α_i
αi和
α
j
α_j
αj,更新截距b的值;
}
4.2.1选择 α i α_i αi和 α j α_j αj:
我们现在是每次迭代都优化目标函数的两个拉格朗日乘子
α
i
α_i
αi和
α
j
α_j
αj,然后其他的拉格朗日乘子保持固定。如果有N个训练样本,我们就有N个拉格朗日乘子需要优化,但每次我们只挑两个进行优化,我们就有N(N-1)种选择。那到底我们要选择哪对
α
i
α_i
αi和
α
j
α_j
αj呢?选择哪对才好呢?想想我们的目标是什么?我们希望把所有违法KKT条件的样本都纠正回来,因为如果所有样本都满足KKT条件的话,我们的优化就完成了。那就很直观了,哪个害群之马最严重,我们得先对他进行思想教育,让他尽早回归正途。OK,我们选择的第一个变量αi就选违法KKT条件最严重的那一个。第二个变量
α
j
α_j
αj选择步长最大的那一个。
1)第一个变量αi的选择:
SMO称选择第一个变量的过程为外层循环。外层训练在训练样本中选取违法KKT条件最严重的样本点。并将其对应的变量作为第一个变量。具体的,检验训练样本
(
x
i
,
y
i
)
(x_i, y_i)
(xi,yi)是否满足KKT条件:
a
i
=
0
⇔
y
i
g
(
x
i
)
>
=
1
a_i=0 {\Leftrightarrow}y_ig(x_i)>=1
ai=0⇔yig(xi)>=1
0
<
a
i
<
C
⇔
y
i
g
(
x
i
)
=
1
0<a_i<C{\Leftrightarrow}y_ig(x_i)=1
0<ai<C⇔yig(xi)=1
a
i
=
C
⇔
y
i
g
(
x
i
)
<
=
1
a_i=C{\Leftrightarrow}y_ig(x_i)<=1
ai=C⇔yig(xi)<=1
其
中
,
g
(
x
i
)
=
∑
i
=
1
N
a
j
y
j
κ
<
x
i
⃗
,
x
j
⃗
>
+
b
其中,g(x_i)=\sum_{i=1}^Na_jy_j\kappa<\vec{x_i},\vec{x_j}>+b
其中,g(xi)=∑i=1Najyjκ<xi,xj>+b
该检验是在 ε ε ε范围内进行的。在检验过程中,外层循环首先遍历所有满足条件 0 < α j < C 0<α_j<C 0<αj<C的样本点,即在间隔边界上的支持向量点,检验他们是否满足KKT条件,然后选择违反KKT条件最严重的 α i α_i αi。如果这些样本点都满足KKT条件,那么遍历整个训练集,检验他们是否满足KKT条件,然后选择违反KKT条件最严重的 α i α_i αi。
优先选择遍历非边界数据样本,因为非边界数据样本更有可能需要调整,边界数据样本常常不能得到进一步调整而留在边界上。由于大部分数据样本都很明显不可能是支持向量,因此对应的α乘子一旦取得零值就无需再调整。遍历非边界数据样本并选出他们当中违反KKT 条件为止。当某一次遍历发现没有非边界数据样本得到调整时,遍历所有数据样本,以检验是否整个集合都满足KKT条件。如果整个集合的检验中又有数据样本被进一步进化,则有必要再遍历非边界数据样本。这样,不停地在遍历所有数据样本和遍历非边界数据样本之间切换,直到整个样本集合都满足KKT条件为止。以上用KKT条件对数据样本所做的检验都以达到一定精度 ε ε ε就可以停止为条件。如果要求十分精确的输出算法,则往往不能很快收敛。
对整个数据集的遍历扫描相当容易,而实现对非边界 α i α_i αi的扫描时,首先需要将所有非边界样本的 α i α_i αi值(也就是满足 0 < α i < C 0<α_i<C 0<αi<C)保存到新的一个列表中,然后再对其进行遍历。同时,该步骤跳过那些已知的不会改变的 α i α_i αi值。
2)第二个变量
α
j
α_j
αj的选择:
在选择第一个
α
i
α_i
αi后,算法会通过一个内循环来选择第二个
α
j
α_j
αj值。因为第二个乘子的迭代步长大致正比于
∣
E
i
−
E
j
∣
|E_i-E_j|
∣Ei−Ej∣,所以我们需要选择能够最大化
∣
E
i
−
E
j
∣
|E_i-E_j|
∣Ei−Ej∣的第二个乘子(选择最大化迭代步长的第二个乘子)。在这里,为了节省计算时间,我们建立一个全局的缓存用于保存所有样本的误差值,而不用每次选择的时候就重新计算。我们从中选择使得步长最大或者
∣
E
i
−
E
j
∣
|E_i-E_j|
∣Ei−Ej∣最大的
α
j
α_j
αj。
4.2.2优化 α i α_i αi和 α j α_j αj:
选择这两个拉格朗日乘子后,我们需要先计算这些参数的约束值。然后再求解这个约束最大化问题。
首先,我们需要给
α
j
α_j
αj找到边界
L
<
=
α
j
<
=
H
L<=α_j<=H
L<=αj<=H,以保证
α
j
α_j
αj满足
0
<
=
α
j
<
=
C
0<=α_j<=C
0<=αj<=C的约束。这意味着
α
j
α_j
αj必须落入这个盒子中。由于只有两个变量
(
α
i
,
α
j
)
(α_i, α_j)
(αi,αj),约束可以用二维空间中的图形来表示,如下图:
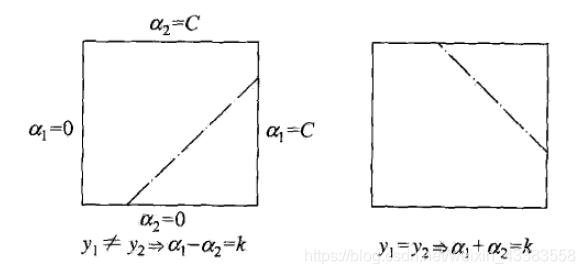
[图9]
不等式约束使得
(
α
i
,
α
j
)
(α_i, α_j)
(αi,αj)在盒子[0, C]x[0, C]内,等式约束使得
(
α
i
,
α
j
)
(α_i, α_j)
(αi,αj)在平行于盒子[0, C]x[0, C]的对角线的直线上。因此要求的是目标函数在一条平行于对角线的线段上的最优值。这使得两个变量的最优化问题成为实质的单变量的最优化问题。由图可以得到,
α
j
α_j
αj的上下界可以通过下面的方法得到:
I
f
y
(
i
)
≠
y
(
j
)
L
=
m
a
x
(
0
,
a
j
−
a
i
)
,
H
=
m
i
n
(
c
,
c
+
a
j
−
a
i
)
If\quad y^{(i)}{\neq}y^{(j)} L=max(0,a_j-a_i),H=min(c,c+a_j-a_i)
Ify(i)̸=y(j)L=max(0,aj−ai),H=min(c,c+aj−ai)
I
f
y
(
i
)
=
y
(
j
)
L
=
m
a
x
(
0
,
a
i
+
a
j
−
C
)
,
H
=
m
i
n
(
c
,
a
i
+
a
j
)
If\quad y^{(i)}=y^{(j)} L=max(0,a_i+a_j-C),H=min(c,a_i+a_j)
Ify(i)=y(j)L=max(0,ai+aj−C),H=min(c,ai+aj)
我们优化的时候, α j α_j αj必须要满足上面这个约束。也就是说上面是 α j α_j αj的可行域。然后我们开始寻找 α j α_j αj,使得目标函数最大化。通过推导得到 α j α_j αj的更新公式如下:
a j : = a j − y ( j ) ( E i − E j ) η a_j:=a_j-\frac{y^{(j)}(E_i-E_j)}{\eta} aj:=aj−ηy(j)(Ei−Ej)
这里 E k E_k Ek可以看做对第k个样本,SVM的输出与期待输出,也就是样本标签的误差。
E
k
=
f
(
x
(
k
)
)
−
y
(
k
)
E_k=f(x^{(k)})-y^{(k)}
Ek=f(x(k))−y(k)
η
=
2
<
x
(
i
)
,
x
(
j
)
>
−
<
x
(
i
)
,
x
(
i
)
>
−
<
x
(
j
)
,
x
(
j
)
>
\eta=2<x^{(i)},x^{(j)}>-<x^{(i)},x^{(i)}>-<x^{(j)},x^{(j)}>
η=2<x(i),x(j)>−<x(i),x(i)>−<x(j),x(j)>
而η实际上是度量两个样本i和j的相似性的。在计算η的时候,我们需要使用核函数,那么就可以用核函数来取代上面的内积。
得到新的
α
j
α_j
αj后,我们需要保证它处于边界内。换句话说,如果这个优化后的值跑出了边界L和H,我们就需要简单的裁剪,将
α
j
α_j
αj收回这个范围:
α
j
:
=
{
H
i
f
a
j
>
H
a
j
i
f
L
<
=
a
j
<
=
H
L
i
f
a
j
<
L
α_j:=\begin{cases} H{\quad} if{\quad}a_j>H \\ a_j{\quad}if{\quad}L<=a_j<=H\\ L {\quad}if{\quad}a_j<L \end{cases}
αj:=⎩⎪⎨⎪⎧Hifaj>HajifL<=aj<=HLifaj<L
最后,得到优化的 α j α_j αj后,我们需要用它来计算 α i α_i αi:
a i : = a i + y ( i ) y ( j ) ( a j o l d − a j ) a_i:=a_i+y^{(i)}y^{(j)}(a_j^{old}-a_j) ai:=ai+y(i)y(j)(ajold−aj)
到这里, α i α_i αi和 α j α_j αj的优化就完成了。
4.2.3计算阈值b:
优化
α
i
α_i
αi和
α
j
α_j
αj后,我们就可以更新阈值b,使得对两个样本i和j都满足KKT条件。如果优化后
α
i
α_i
αi不在边界上(也就是满足
0
<
α
i
<
C
0<α_i<C
0<αi<C,这时候根据KKT条件,可以得到
y
i
g
i
(
x
i
)
=
1
y_ig_i(x_i)=1
yigi(xi)=1,这样我们才可以计算
b
b
b),那下面的阈值
b
1
b1
b1是有效的,因为当输入
x
i
x_i
xi时它迫使SVM输出
y
i
y_i
yi。
b
1
:
=
b
−
E
i
−
y
(
i
)
(
a
i
−
a
i
(
o
l
d
)
)
<
x
(
i
)
,
x
(
i
)
>
−
y
(
j
)
(
a
j
−
a
j
(
o
l
d
)
<
x
(
i
)
,
x
(
j
)
>
b1:=b-E_i-y^{(i)}(a_i-a_i^{(old)})<x^{(i)},x^{(i)}>-y^{(j)}(a_j-a_j^{(old)}<x^{(i)},x^{(j)}>
b1:=b−Ei−y(i)(ai−ai(old))<x(i),x(i)>−y(j)(aj−aj(old)<x(i),x(j)>
同样,如果
0
<
α
j
<
C
0<α_j<C
0<αj<C,那么下面的b2也是有效的:
b
2
=
b
−
E
j
−
y
(
i
)
(
a
i
−
a
i
(
o
l
d
)
)
<
x
(
i
)
,
x
(
j
)
>
−
y
(
j
)
(
a
j
−
a
j
(
o
l
d
)
)
<
x
(
j
)
,
x
(
j
)
>
b2=b-E_j-y^{(i)}(a_i-a_i^{(old)})<x^{(i)},x^{(j)}>-y^{(j)}(a_j-a_j^{(old)})<x^{(j)},x^{(j)}>
b2=b−Ej−y(i)(ai−ai(old))<x(i),x(j)>−y(j)(aj−aj(old))<x(j),x(j)>
如果
0
<
α
i
<
C
0<α_i<C
0<αi<C和
0
<
α
j
<
C
0<α_j<C
0<αj<C都满足,那么b1和b2都有效,而且他们是相等的。如果他们两个都处于边界上(也就是
α
i
α_i
αi=0或者
α
i
=
C
α_i=C
αi=C,同时
α
j
=
0
α_j=0
αj=0或者
α
j
=
C
α_j=C
αj=C),那么在b1和b2之间的阈值都满足KKT条件,一般我们取他们的平均值
b
=
(
b
1
+
b
2
)
/
2
b=(b1+b2)/2
b=(b1+b2)/2。所以,总的来说对b的更新如下:
b
:
=
{
b
1
i
f
0
<
a
i
<
C
b
2
i
f
0
<
a
j
<
C
(
b
1
+
b
2
)
/
2
o
t
h
e
r
w
i
s
e
b:=\begin{cases} b1{\quad} if{\quad}0<a_i<C \\ b2{\quad}if{\quad}0<a_j<C\\ (b1+b2)/2 {\quad} otherwise \end{cases}
b:=⎩⎪⎨⎪⎧b1if0<ai<Cb2if0<aj<C(b1+b2)/2otherwise
每做完一次最小优化,必须更新每个数据样本的误差,以便用修正过的分类面对其他数据样本再做检验,在选择第二个配对优化数据样本时用来估计步长。
4.2.4凸优化问题终止条件:
SMO算法的基本思路是:如果说有变量的解都满足此最优化问题的KKT条件,那么这个最优化问题的解就得到了。因为KKT条件是该最优化问题的充分必要条件(证明请参考文献)。所以我们可以监视原问题的KKT条件,所以所有的样本都满足KKT条件,那么就表示迭代结束了。但是由于KKT条件本身是比较苛刻的,所以也需要设定一个容忍值,即所有样本在容忍值范围内满足KKT条件则认为训练可以结束;当然了,对于对偶问题的凸优化还有其他终止条件,可以参考文献。注意:SMO算法只是求解SVM的其中一种方法,大家在学习SVM过程中不必过于纠结SMO算法编程实现,只需要将理论思想理解即可。
4.2.5Python实现完整SMO算法核心代码
寻找第2个步长最大的alphas[j]:
# 寻找第2个步长最大的alphas[j]
def selectJ(i, oS, Ei): #this is the second choice -heurstic, and calcs Ej
maxK = -1; maxDeltaE = 0; Ej = 0
oS.eCache[i] = [1,Ei] #set valid #choose the alpha that gives the maximum delta E
validEcacheList = np.nonzero(oS.eCache[:,0].A)[0]
if (len(validEcacheList)) > 1:
for k in validEcacheList: #loop through valid Ecache values and find the one that maximizes delta E
if k == i: continue #don't calc for i, waste of time
Ek = calcEk(oS, k)
deltaE = abs(Ei - Ek)
if (deltaE > maxDeltaE):
maxK = k; maxDeltaE = deltaE; Ej = Ek
return maxK, Ej
else: #in this case (first time around) we don't have any valid eCache values
j = selectJrand(i, oS.m)
Ej = calcEk(oS, j)
return j, Ej
SMO主函数:
# SMO主函数
def smoP(dataMatIn, classLabels, C, toler, maxIter,kTup=('lin', 0)): #full Platt SMO
oS = optStruct(np.mat(dataMatIn),np.mat(classLabels).transpose(),C,toler, kTup)
iter = 0
entireSet = True; alphaPairsChanged = 0
while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):
alphaPairsChanged = 0
if entireSet: #go over all
for i in range(oS.m):
alphaPairsChanged += innerL(i,oS)
#print( "fullSet, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged))
iter += 1
else:#go over non-bound (railed) alphas
nonBoundIs = np.nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]
for i in nonBoundIs:
alphaPairsChanged += innerL(i,oS)
#print( "non-bound, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged))
iter += 1
if entireSet: entireSet = False #toggle entire set loop
elif (alphaPairsChanged == 0): entireSet = True
#print( "iteration number: %d" % iter)
return oS.b,oS.alphas
SMO完整代码输出结果:
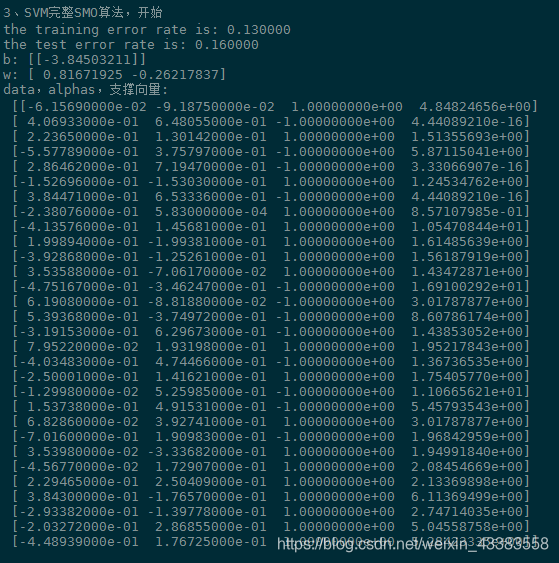
[图10]
5.完整源代码
# -*- coding: utf-8 -*-
"""
@Time : 2018/11/25 19:42
@Author : hanzi5
@Email : hanzi5@yeah.net
@File : SVM.py
@Software: PyCharm
"""
import numpy as np
#import pandas as pd
from scipy.optimize import fmin_l_bfgs_b
from scipy.optimize import fmin_tnc
#from scipy.optimize import fmin_bfgs
import matplotlib.pyplot as plt
import matplotlib
from matplotlib.patches import Circle
matplotlib.rcParams['font.family']='SimHei' # 用来正常显示中文
plt.rcParams['axes.unicode_minus']=False # 用来正常显示负号
# 定义目标函数,w是未知数据,args是已知数,求w的最优解
def func(w,*args):
X,Y,c=args
yp=np.dot(X,w) # w*x,注意已经将b作为x的第一列进行了计算,w*x就是我们现在预测的y
idx=np.where(yp*Y<1)[0] # 找到分错的数据索引位置
e=yp[idx]-Y[idx] # y预测值-y真实值,误差
cost=np.dot(e,e)+c*np.dot(w,w) # 平方和损失,c:学习率,加w的二范式惩罚
grand=2*(np.dot(X[idx].T,e)+c*w)# 梯度下降??
return cost,grand
def plotResult(w):
margin=2/np.sqrt(np.dot(w[1:3],w[1:3]))
plot_x=np.append(np.min(x,0)[0]-0.2,np.max(x,0)[0]+0.2)
plot_y=-(plot_x*w[1]+w[0])/w[2]
plt.figure()
pos=(Y==1) # 正类
neg=(y==-1) # 负类
plt.plot(x[pos][:,0],x[pos][:,1],"r+",label="正类")
plt.plot(x[neg][:,0],x[neg][:,1],"bo",label="负类")
plt.plot(plot_x,plot_y,"r-",label="分割超平面")
plt.plot(plot_x,plot_y+margin/2,"g-.",label="")
plt.plot(plot_x,plot_y-margin/2,"g-.",label="")
plt.xlabel('x1')
plt.ylabel('x2')
plt.title('SVM Demo')
plt.legend()
plt.show()
# 简易smo算法开始####################################################################
# 随机选择第2个alpha
def selectJrand(i,m):
j=i #we want to select any J not equal to i
while (j==i):
j = int(np.random.uniform(0,m))
return j
# 调整大于H或小于L的alpha值
def clipAlpha(aj,H,L):
if aj > H:
aj = H
if L > aj:
aj = L
return aj
# 公共函数,根据公式求w,简易smo算法及完整smo算法通用
def calcWs(alphas,dataArr,labelArr):
w=sum( np.array(alphas) * np.array(labelArr.reshape((-1,1))) * np.array(np.array(dataArr)) )
return w
# 输入变量:x、y、c:常数c、toler:容错率、maxIter:最大循环次数
def smoSimple(dataMatIn, classLabels, C, toler, maxIter):
#dataMatIn, classLabels, C, toler, maxIter=dataArr,lableArr,0.6,0.001,40
dataMatrix = np.mat(dataMatIn) # 数据x转换为matrix类型
labelMat = np.mat(classLabels).transpose() # 标签y转换为matrix类型,转换为一列
b = 0 # 截距b
m,n = np.shape(dataMatrix) # 数据x行数、列数
alphas = np.mat(np.zeros((m,1))) # 初始化alpha,有多少行数据就产生多少个alpha
iter = 0 # 遍历计数器
while (iter < maxIter):
#print( "iteration number: %d" % iter)
alphaPairsChanged = 0 # 记录alpha是否已被优化,每次循环都重置
for i in range(m): # 按行遍历数据,类似随机梯度下降
# i=0
fXi = float(np.multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[i,:].T)) + b # 预测值y,g(x)函数,《统计学习方法》李航P127,7.104
Ei = fXi - float(labelMat[i])#if checks if an example violates KKT conditions # 误差,Ei函数,P127,7.105
if ((labelMat[i]*Ei < -toler) and (alphas[i] < C)) or ((labelMat[i]*Ei > toler) and (alphas[i] > 0)):
# 找第一个alphas[i],找到第一个满足判断条件的,判断负间隔or正间隔,并且保证0<alphas<C
j = selectJrand(i,m) # 随机找到第二个alphas[j]
fXj = float(np.multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[j,:].T)) + b # 计算预测值
Ej = fXj - float(labelMat[j]) # 计算alphas[j]误差
alphaIold = alphas[i].copy() # 记录上一次alphas[i]值
alphaJold = alphas[j].copy() # 记录上一次alphas[j]值
if (labelMat[i] != labelMat[j]):# 计算H及L值,《统计学习方法》李航,P126
L = max(0, alphas[j] - alphas[i])
H = min(C, C + alphas[j] - alphas[i])
else:
L = max(0, alphas[j] + alphas[i] - C)
H = min(C, alphas[j] + alphas[i])
if L==H:
#print( "L==H")
continue
eta = 2.0 * dataMatrix[i,:]*dataMatrix[j,:].T - dataMatrix[i,:]*dataMatrix[i,:].T - dataMatrix[j,:]*dataMatrix[j,:].T
# 《统计学习方法》李航P127,7.107,这里的eta与李航的一致,这里乘了负号
if eta >= 0:
#print("eta>=0")
continue
alphas[j] -= labelMat[j]*(Ei - Ej)/eta # 《统计学习方法》李航P127,7.107,更新alphas[j]
alphas[j] = clipAlpha(alphas[j],H,L) # alphas[j]调整大于H或小于L的alpha值
if (abs(alphas[j] - alphaJold) < 0.00001): # 调整后过小,则不更新alphas[i]
#print( "j not moving enough")
continue
alphas[i] += labelMat[j]*labelMat[i]*(alphaJold - alphas[j]) #更新alphas[i],《统计学习方法》李航P127,7.109
# 更新b值,《统计学习方法》李航P130,7.115,7.116
b1 = b - Ei- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[i,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[i,:]*dataMatrix[j,:].T
b2 = b - Ej- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[j,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[j,:]*dataMatrix[j,:].T
if (0 < alphas[i]) and (C > alphas[i]): # 判断符合条件的b
b = b1
elif (0 < alphas[j]) and (C > alphas[j]):
b = b2
else:
b = (b1 + b2)/2.0
alphaPairsChanged += 1
#print( "iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged))
if (alphaPairsChanged == 0):
iter += 1
else:
iter = 0
return b,alphas
# 画图
def plot_smoSimple(dataArrWithAlpha,b,w):
type1_x1 = []
type1_x2 = []
type2_x1 = []
type2_x2 = []
dataSet=dataArrWithAlpha
# 取两类x1及x2值画图
type1_x1=dataSet[dataSet[:,-2]==-1][:,:-2][:,0].tolist()
type1_x2=dataSet[dataSet[:,-2]==-1][:,:-2][:,1].tolist()
type2_x1=dataSet[dataSet[:,-2]==1][:,:-2][:,0].tolist()
type2_x2=dataSet[dataSet[:,-2]==1][:,:-2][:,1].tolist()
# 画点
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(type1_x1,type1_x2, marker='s', s=90)
ax.scatter(type2_x1,type2_x2, marker='o', s=50, c='red')
plt.title('Support Vectors Circled')
# 获取支持向量值,画椭圆
dataVectors=dataArrWithAlpha[dataArrWithAlpha[:,-1]>0]
for d in dataVectors:
circle = Circle(d[0:2], 0.5, facecolor='none', edgecolor=(0,0.8,0.8), linewidth=3, alpha=0.5)
ax.add_patch(circle)
# 画分割超平面
b=b1.getA()[0][0] # 获得传入的b
w0= w[0]#0.8065
w1= w[1]#-0.2761
x = np.arange(-2.0, 12.0, 0.1)
y = (-w0*x - b)/w1
ax.plot(x,y)
ax.axis([-2,12,-8,6])
plt.show()
# 简易smo算法结束####################################################################
# 完整smo算法开始####################################################################
class optStruct:
def __init__(self,dataMatIn, classLabels, C, toler, kTup): # Initialize the structure with the parameters
self.X = dataMatIn
self.labelMat = classLabels
self.C = C
self.tol = toler
self.m = np.shape(dataMatIn)[0]
self.alphas = np.mat(np.zeros((self.m,1)))
self.b = 0
self.eCache = np.mat(np.zeros((self.m,2))) #first column is valid flag
self.K = np.mat(np.zeros((self.m,self.m)))
for i in range(self.m):
self.K[:,i] = kernelTrans(self.X, self.X[i,:], kTup)
# 核函数
def kernelTrans(X, A, kTup): #calc the kernel or transform data to a higher dimensional space
m,n = np.shape(X)
K = np.mat(np.zeros((m,1)))
if kTup[0]=='lin': K = X * A.T #linear kernel
elif kTup[0]=='rbf':
for j in range(m):
deltaRow = X[j,:] - A
K[j] = deltaRow*deltaRow.T
K = np.exp(K/(-1*kTup[1]**2)) #divide in NumPy is element-wise not matrix like Matlab
else: raise NameError('Houston We Have a Problem -- \
That Kernel is not recognized')
return K
# 计算误差
def calcEk(oS, k):
fXk = float(np.multiply(oS.alphas,oS.labelMat).T*oS.K[:,k] + oS.b)
Ek = fXk - float(oS.labelMat[k])
return Ek
# 寻找第2个步长最大的alphas[j]
def selectJ(i, oS, Ei): #this is the second choice -heurstic, and calcs Ej
maxK = -1; maxDeltaE = 0; Ej = 0
oS.eCache[i] = [1,Ei] #set valid #choose the alpha that gives the maximum delta E
validEcacheList = np.nonzero(oS.eCache[:,0].A)[0]
if (len(validEcacheList)) > 1:
for k in validEcacheList: #loop through valid Ecache values and find the one that maximizes delta E
if k == i: continue #don't calc for i, waste of time
Ek = calcEk(oS, k)
deltaE = abs(Ei - Ek)
if (deltaE > maxDeltaE):
maxK = k; maxDeltaE = deltaE; Ej = Ek
return maxK, Ej
else: #in this case (first time around) we don't have any valid eCache values
j = selectJrand(i, oS.m)
Ej = calcEk(oS, j)
return j, Ej
# 计算误差存入缓存中
def updateEk(oS, k):#after any alpha has changed update the new value in the cache
Ek = calcEk(oS, k)
oS.eCache[k] = [1,Ek]
# 内循环,寻找第2个步长最大的alphas[j]
def innerL(i, oS):
Ei = calcEk(oS, i)
if ((oS.labelMat[i]*Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i]*Ei > oS.tol) and (oS.alphas[i] > 0)):
j,Ej = selectJ(i, oS, Ei) #this has been changed from selectJrand
alphaIold = oS.alphas[i].copy(); alphaJold = oS.alphas[j].copy();
if (oS.labelMat[i] != oS.labelMat[j]):
L = max(0, oS.alphas[j] - oS.alphas[i])
H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
else:
L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
H = min(oS.C, oS.alphas[j] + oS.alphas[i])
if L==H:
#print ("L==H")
return 0
eta = 2.0 * oS.K[i,j] - oS.K[i,i] - oS.K[j,j] #changed for kernel
if eta >= 0:
#print( "eta>=0")
return 0
oS.alphas[j] -= oS.labelMat[j]*(Ei - Ej)/eta
oS.alphas[j] = clipAlpha(oS.alphas[j],H,L)
updateEk(oS, j) #added this for the Ecache
if (abs(oS.alphas[j] - alphaJold) < 0.00001):
#print( "j not moving enough")
return 0
oS.alphas[i] += oS.labelMat[j]*oS.labelMat[i]*(alphaJold - oS.alphas[j])#update i by the same amount as j
updateEk(oS, i) #added this for the Ecache #the update is in the oppostie direction
b1 = oS.b - Ei- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,i] - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[i,j]
b2 = oS.b - Ej- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,j]- oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[j,j]
if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]): oS.b = b1
elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]): oS.b = b2
else: oS.b = (b1 + b2)/2.0
return 1
else: return 0
# SMO主函数
def smoP(dataMatIn, classLabels, C, toler, maxIter,kTup=('lin', 0)): #full Platt SMO
oS = optStruct(np.mat(dataMatIn),np.mat(classLabels).transpose(),C,toler, kTup)
iter = 0
entireSet = True; alphaPairsChanged = 0
while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):
alphaPairsChanged = 0
if entireSet: #go over all
for i in range(oS.m):
alphaPairsChanged += innerL(i,oS)
#print( "fullSet, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged))
iter += 1
else:#go over non-bound (railed) alphas
nonBoundIs = np.nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]
for i in nonBoundIs:
alphaPairsChanged += innerL(i,oS)
#print( "non-bound, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged))
iter += 1
if entireSet: entireSet = False #toggle entire set loop
elif (alphaPairsChanged == 0): entireSet = True
#print( "iteration number: %d" % iter)
return oS.b,oS.alphas
# 测试Rbf数据
def testRbf(dataArrTrain,labelArrTrain,dataArrTest,labelArrTest,k1=1.3):
b,alphas = smoP(dataArrTrain, labelArrTrain, 200, 0.0001, 10000, ('rbf', k1)) #C=200 important
datMat=np.mat(dataArrTrain); labelArrTrain = np.mat(labelArrTrain).transpose()
svInd=np.nonzero(alphas.A>0)[0]
sVs=datMat[svInd] #get matrix of only support vectors
labelSV = labelArrTrain[svInd];
#print( "there are %d Support Vectors" % np.shape(sVs)[0])
m,n = np.shape(datMat)
errorCount = 0
for i in range(m):
kernelEval = kernelTrans(sVs,datMat[i,:],('rbf', k1))
predict=kernelEval.T * np.multiply(labelSV,alphas[svInd]) + b
if np.sign(predict)!=np.sign(labelArrTrain[i]): errorCount += 1
print( "the training error rate is: %f" % (float(errorCount)/m))
errorCount = 0
datMat=np.mat(dataArrTest)
#labelMat = np.mat(labelArrTest).transpose()
m,n = np.shape(datMat)
for i in range(m):
kernelEval = kernelTrans(sVs,datMat[i,:],('rbf', k1))
predict=kernelEval.T * np.multiply(labelSV,alphas[svInd]) + b
if np.sign(predict)!=np.sign(labelArrTest[i]): errorCount += 1
print( "the test error rate is: %f" % (float(errorCount)/m) )
return b,alphas
# 画图,rbf核函数数据
def plot_smoCompletion ():
xcord0 = []; ycord0 = []; xcord1 = []; ycord1 = []
fw = open('D:/python_data/testSetRBF2.txt', 'w')#generate data
fig = plt.figure()
ax = fig.add_subplot(111)
xcord0 = []; ycord0 = []; xcord1 = []; ycord1 = []
for i in range(100):
[x,y] = np.random.uniform(0,1,2)
xpt=x*np.cos(2.0*np.pi*y); ypt = x*np.sin(2.0*np.pi*y)
if (x > 0.5):
xcord0.append(xpt); ycord0.append(ypt)
label = -1.0
else:
xcord1.append(xpt); ycord1.append(ypt)
label = 1.0
fw.write('%f\t%f\t%f\n' % (xpt, ypt, label))
ax.scatter(xcord0,ycord0, marker='s', s=90)
ax.scatter(xcord1,ycord1, marker='o', s=50, c='red')
plt.title('Non-linearly Separable Data for Kernel Method')
plt.show()
fw.close()
# 完整smo算法结束####################################################################
if __name__ == '__main__':
##1、SVM直接求参数值#############################################################
print('\n1、SVM直接求参数值,开始')
# 生成数据,《统计学习方法》李航,P103,例7.1
dataSet=np.array([[3,3,1],[4,3,1],[1,1,-1]]) # ,[0,0,-1],[0,1,-1]
m, n = dataSet.shape
x=dataSet[:,:-1]
y=dataSet[:,-1] #.reshape((-1,1))
# 数据定义
X=np.append(np.ones([x.shape[0],1]),x,1) # x新增一列全1值,作为截距b
Y=y
c=0.001 # 学习率
w=np.zeros(X.shape[1]) # 初始化一组w系数,全0,也可随机产生:np.random.rand(X.shape[1])
# bfgs_b方法求最优化问题
REF=fmin_l_bfgs_b(func,x0=w,args=(X,Y,c),approx_grad=False) #x0=np.random.rand(X.shape[1]) [0,0,0]
# 采用scipy.optimize其他包夜可以求得
REF2=fmin_tnc(func,x0=w,args=(X,Y,c),approx_grad=False)
# 求得最优化计算后的w
w=REF[0].round(2) # 取得w值
print('w:',w[1:],'b:',w[0]) # 与《统计学习方法》李航,P103,例7.1计算结果一致
# 画图
plotResult(w)
print('\n1、SVM直接求参数值,结束')
##2、SVM简易SMO算法#############################################################
print('\n2、SVM简易SMO算法,开始')
fileIn = 'D:/python_data/testSet.txt'
#dataSet=pd.read_table(fileIn,names=['x1','x2','y']).values
dataSet=np.loadtxt(fileIn)
dataArr=dataSet[:,:-1] # x
labelArr=dataSet[:,-1] # y
b1,alphas1=smoSimple(dataArr,labelArr,0.6,0.001,50) # 输入变量:x、y、c:常数c、toler:容错率、maxIter:最大循环次数
dataArrWithAlpha1=np.array(np.concatenate((dataSet,alphas1),axis=1)) # 把alphas1与原始数据合并
w1=calcWs(alphas1,dataArr,labelArr) # 根据alpha求w
print('b:',b1,'\nw:',w1,'\ndata,alphas,支撑向量:\n',dataArrWithAlpha1[dataArrWithAlpha1[:,-1]>0] )# 注意这里的筛选方式与pd.DataFrame筛选方式一致,array类型的才可以这样写,np.ndarray及np.matrix类型不可以使用
plot_smoSimple(dataArrWithAlpha1,b1,w1) # 画图
print('2、SVM简易SMO算法,结束')
##3、SVM完整SMO算法#############################################################
print('\n3、SVM完整SMO算法,开始')
dataSetTrain = np.loadtxt('D:/python_data/testSetRBF.txt')
dataSetTest = np.loadtxt('D:/python_data/testSetRBF2.txt')
# 训练集
dataArrTrain=dataSetTrain[:,:-1] # 训练集x
labelArrTrain=dataSetTrain[:,-1] # 训练集y
# 测试集
dataArrTest=dataSetTest[:,:-1] # 测试集x
labelArrTest=dataSetTest[:,-1] # 测试集y
# 调用主函数
b2,alphas2=testRbf(dataArrTrain,labelArrTrain,dataArrTest,labelArrTest,k1=1.3)
w2=calcWs(alphas2,dataArrTrain,labelArrTrain) # 根据alpha求w
dataArrWithAlpha2=np.array(np.concatenate((dataSetTrain,alphas2),axis=1)) # 把alphas1与原始数据合并
print('b:',b1,'\nw:',w1,'\ndata,alphas,支撑向量:\n',dataArrWithAlpha2[dataArrWithAlpha2[:,-1]>0] )# 注意这里的筛选方式与pd.DataFrame筛选方式一致,array类型的才可以这样写,np.ndarray及np.matrix类型不可以使用
plot_smoCompletion() # 画图,训练集
print('3、SVM完整SMO算法,结束')
数据,testSet.txt
3.542485 1.977398 -1
3.018896 2.556416 -1
7.551510 -1.580030 1
2.114999 -0.004466 -1
8.127113 1.274372 1
7.108772 -0.986906 1
8.610639 2.046708 1
2.326297 0.265213 -1
3.634009 1.730537 -1
0.341367 -0.894998 -1
3.125951 0.293251 -1
2.123252 -0.783563 -1
0.887835 -2.797792 -1
7.139979 -2.329896 1
1.696414 -1.212496 -1
8.117032 0.623493 1
8.497162 -0.266649 1
4.658191 3.507396 -1
8.197181 1.545132 1
1.208047 0.213100 -1
1.928486 -0.321870 -1
2.175808 -0.014527 -1
7.886608 0.461755 1
3.223038 -0.552392 -1
3.628502 2.190585 -1
7.407860 -0.121961 1
7.286357 0.251077 1
2.301095 -0.533988 -1
-0.232542 -0.547690 -1
3.457096 -0.082216 -1
3.023938 -0.057392 -1
8.015003 0.885325 1
8.991748 0.923154 1
7.916831 -1.781735 1
7.616862 -0.217958 1
2.450939 0.744967 -1
7.270337 -2.507834 1
1.749721 -0.961902 -1
1.803111 -0.176349 -1
8.804461 3.044301 1
1.231257 -0.568573 -1
2.074915 1.410550 -1
-0.743036 -1.736103 -1
3.536555 3.964960 -1
8.410143 0.025606 1
7.382988 -0.478764 1
6.960661 -0.245353 1
8.234460 0.701868 1
8.168618 -0.903835 1
1.534187 -0.622492 -1
9.229518 2.066088 1
7.886242 0.191813 1
2.893743 -1.643468 -1
1.870457 -1.040420 -1
5.286862 -2.358286 1
6.080573 0.418886 1
2.544314 1.714165 -1
6.016004 -3.753712 1
0.926310 -0.564359 -1
0.870296 -0.109952 -1
2.369345 1.375695 -1
1.363782 -0.254082 -1
7.279460 -0.189572 1
1.896005 0.515080 -1
8.102154 -0.603875 1
2.529893 0.662657 -1
1.963874 -0.365233 -1
8.132048 0.785914 1
8.245938 0.372366 1
6.543888 0.433164 1
-0.236713 -5.766721 -1
8.112593 0.295839 1
9.803425 1.495167 1
1.497407 -0.552916 -1
1.336267 -1.632889 -1
9.205805 -0.586480 1
1.966279 -1.840439 -1
8.398012 1.584918 1
7.239953 -1.764292 1
7.556201 0.241185 1
9.015509 0.345019 1
8.266085 -0.230977 1
8.545620 2.788799 1
9.295969 1.346332 1
2.404234 0.570278 -1
2.037772 0.021919 -1
1.727631 -0.453143 -1
1.979395 -0.050773 -1
8.092288 -1.372433 1
1.667645 0.239204 -1
9.854303 1.365116 1
7.921057 -1.327587 1
8.500757 1.492372 1
1.339746 -0.291183 -1
3.107511 0.758367 -1
2.609525 0.902979 -1
3.263585 1.367898 -1
2.912122 -0.202359 -1
1.731786 0.589096 -1
2.387003 1.573131 -1
testSetRBF.txt
-0.214824 0.662756 -1.000000
-0.061569 -0.091875 1.000000
0.406933 0.648055 -1.000000
0.223650 0.130142 1.000000
0.231317 0.766906 -1.000000
-0.748800 -0.531637 -1.000000
-0.557789 0.375797 -1.000000
0.207123 -0.019463 1.000000
0.286462 0.719470 -1.000000
0.195300 -0.179039 1.000000
-0.152696 -0.153030 1.000000
0.384471 0.653336 -1.000000
-0.117280 -0.153217 1.000000
-0.238076 0.000583 1.000000
-0.413576 0.145681 1.000000
0.490767 -0.680029 -1.000000
0.199894 -0.199381 1.000000
-0.356048 0.537960 -1.000000
-0.392868 -0.125261 1.000000
0.353588 -0.070617 1.000000
0.020984 0.925720 -1.000000
-0.475167 -0.346247 -1.000000
0.074952 0.042783 1.000000
0.394164 -0.058217 1.000000
0.663418 0.436525 -1.000000
0.402158 0.577744 -1.000000
-0.449349 -0.038074 1.000000
0.619080 -0.088188 -1.000000
0.268066 -0.071621 1.000000
-0.015165 0.359326 1.000000
0.539368 -0.374972 -1.000000
-0.319153 0.629673 -1.000000
0.694424 0.641180 -1.000000
0.079522 0.193198 1.000000
0.253289 -0.285861 1.000000
-0.035558 -0.010086 1.000000
-0.403483 0.474466 -1.000000
-0.034312 0.995685 -1.000000
-0.590657 0.438051 -1.000000
-0.098871 -0.023953 1.000000
-0.250001 0.141621 1.000000
-0.012998 0.525985 -1.000000
0.153738 0.491531 -1.000000
0.388215 -0.656567 -1.000000
0.049008 0.013499 1.000000
0.068286 0.392741 1.000000
0.747800 -0.066630 -1.000000
0.004621 -0.042932 1.000000
-0.701600 0.190983 -1.000000
0.055413 -0.024380 1.000000
0.035398 -0.333682 1.000000
0.211795 0.024689 1.000000
-0.045677 0.172907 1.000000
0.595222 0.209570 -1.000000
0.229465 0.250409 1.000000
-0.089293 0.068198 1.000000
0.384300 -0.176570 1.000000
0.834912 -0.110321 -1.000000
-0.307768 0.503038 -1.000000
-0.777063 -0.348066 -1.000000
0.017390 0.152441 1.000000
-0.293382 -0.139778 1.000000
-0.203272 0.286855 1.000000
0.957812 -0.152444 -1.000000
0.004609 -0.070617 1.000000
-0.755431 0.096711 -1.000000
-0.526487 0.547282 -1.000000
-0.246873 0.833713 -1.000000
0.185639 -0.066162 1.000000
0.851934 0.456603 -1.000000
-0.827912 0.117122 -1.000000
0.233512 -0.106274 1.000000
0.583671 -0.709033 -1.000000
-0.487023 0.625140 -1.000000
-0.448939 0.176725 1.000000
0.155907 -0.166371 1.000000
0.334204 0.381237 -1.000000
0.081536 -0.106212 1.000000
0.227222 0.527437 -1.000000
0.759290 0.330720 -1.000000
0.204177 -0.023516 1.000000
0.577939 0.403784 -1.000000
-0.568534 0.442948 -1.000000
-0.011520 0.021165 1.000000
0.875720 0.422476 -1.000000
0.297885 -0.632874 -1.000000
-0.015821 0.031226 1.000000
0.541359 -0.205969 -1.000000
-0.689946 -0.508674 -1.000000
-0.343049 0.841653 -1.000000
0.523902 -0.436156 -1.000000
0.249281 -0.711840 -1.000000
0.193449 0.574598 -1.000000
-0.257542 -0.753885 -1.000000
-0.021605 0.158080 1.000000
0.601559 -0.727041 -1.000000
-0.791603 0.095651 -1.000000
-0.908298 -0.053376 -1.000000
0.122020 0.850966 -1.000000
-0.725568 -0.292022 -1.000000
testSetRBF2.txt
-0.117432 -0.772533 -1.000000
0.424996 0.685671 -1.000000
-0.366447 -0.032439 1.000000
-0.456538 -0.326062 -1.000000
-0.753378 -0.060207 -1.000000
-0.737534 0.087643 -1.000000
-0.093421 -0.126775 1.000000
-0.351430 0.926426 -1.000000
0.012625 -0.190257 1.000000
-0.351591 0.693200 -1.000000
0.388269 -0.852720 -1.000000
0.142043 0.318140 1.000000
0.264801 -0.401142 1.000000
0.136152 -0.090225 1.000000
0.974734 0.016945 -1.000000
0.244563 0.488831 -1.000000
-0.280123 -0.056987 1.000000
0.091556 -0.081223 1.000000
-0.090611 -0.016636 1.000000
-0.813602 -0.266067 -1.000000
-0.000300 0.000043 1.000000
0.242741 0.303703 1.000000
-0.817048 -0.008500 -1.000000
0.529506 0.798931 -1.000000
0.524553 -0.567558 -1.000000
0.381955 0.001980 1.000000
-0.602431 0.473769 -1.000000
0.231215 -0.234673 1.000000
-0.749613 -0.345047 -1.000000
0.224492 0.182258 1.000000
0.172463 -0.513747 -1.000000
0.147603 0.910376 -1.000000
0.734239 -0.286891 -1.000000
0.154865 -0.548473 -1.000000
-0.147829 0.009083 1.000000
-0.017590 -0.044190 1.000000
0.440672 0.691269 -1.000000
-0.357727 0.550873 -1.000000
0.457356 0.133797 1.000000
0.232346 -0.239350 1.000000
0.478807 0.852203 -1.000000
-0.026059 0.040957 1.000000
0.775044 -0.460803 -1.000000
-0.267704 -0.306558 1.000000
-0.855806 0.110270 -1.000000
0.480211 -0.521624 -1.000000
0.765252 -0.047894 -1.000000
-0.644040 0.586377 -1.000000
-0.110076 0.719103 -1.000000
0.133619 0.524928 -1.000000
-0.173815 0.732079 -1.000000
0.942163 0.221746 -1.000000
-0.687198 0.047586 -1.000000
0.630384 0.281265 -1.000000
0.038130 0.010993 1.000000
-0.008068 -0.118929 1.000000
0.534217 0.111413 -1.000000
-0.325657 0.273019 1.000000
-0.015575 0.736060 -1.000000
-0.333588 -0.932616 -1.000000
0.348827 0.863883 -1.000000
0.442462 0.389002 -1.000000
-0.101086 0.128123 1.000000
0.097092 0.321638 1.000000
0.125921 0.621098 -1.000000
-0.357218 0.095364 1.000000
0.803109 0.081817 -1.000000
-0.514764 -0.111062 -1.000000
0.047659 -0.176539 1.000000
-0.007704 0.044554 1.000000
-0.472410 -0.592451 -1.000000
-0.197716 -0.791531 -1.000000
-0.515508 -0.339354 -1.000000
0.642045 0.251044 -1.000000
-0.065945 -0.162388 1.000000
-0.744879 -0.045031 -1.000000
0.209621 0.472639 -1.000000
-0.544970 -0.167653 -1.000000
-0.431730 0.679799 -1.000000
0.542874 -0.724989 -1.000000
0.074219 0.805839 -1.000000
0.451146 -0.375435 -1.000000
0.743191 0.606076 -1.000000
0.529628 -0.195778 -1.000000
0.368259 0.348836 -1.000000
-0.933910 -0.214162 -1.000000
-0.119933 -0.518656 -1.000000
-0.627876 0.753061 -1.000000
-0.116855 -0.127113 1.000000
0.061212 -0.019597 1.000000
0.897120 -0.198540 -1.000000
-0.469099 0.232863 -1.000000
-0.212642 0.637247 -1.000000
0.012848 0.035170 1.000000
0.652035 -0.129829 -1.000000
-0.001256 0.719979 -1.000000
0.921166 -0.204044 -1.000000
-0.844109 -0.536146 -1.000000
0.428299 -0.813288 -1.000000
0.731897 -0.242729 -1.000000
参考资料:
1、《机器学习实战》Peter Harrington著
2、《机器学习》西瓜书,周志华著
3、 斯坦福大学公开课 :机器学习课程
4、机器学习视频,邹博
5、《统计学习方法》李航
6、SVM GarryLau
7、机器学习算法与Python实践之(二、三、四) zouxy09





 本文深入探讨了支持向量机(SVM)的概念及其在不同场景下的应用,包括线性可分、线性近似可分和非线性分类问题。详细讲解了SVM的数学原理,包括硬间隔和软间隔最大化,并介绍了SVM在实际问题中的稳定性与广泛的应用领域。此外,还提供了SVM算法的Python实现示例,涵盖了直接求参数值、简易SMO算法和完整SMO算法。
本文深入探讨了支持向量机(SVM)的概念及其在不同场景下的应用,包括线性可分、线性近似可分和非线性分类问题。详细讲解了SVM的数学原理,包括硬间隔和软间隔最大化,并介绍了SVM在实际问题中的稳定性与广泛的应用领域。此外,还提供了SVM算法的Python实现示例,涵盖了直接求参数值、简易SMO算法和完整SMO算法。
















 362
362

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








