八皇后问题

问题起源：
西洋棋中的皇后可以直线，斜线吃掉所遇到的棋子，如果在88的棋盘上有八个皇后，则这八个皇后如何相安无事的摆放在棋盘上？1970年与1971年，E.W.Dijkstra与N.Wirth曾经用这个问题来讲解程式设计之技巧。
88的棋盘，需要在这个棋盘上摆放8个皇后（相同横、竖、斜线上不能再有皇后），求一种有多少种不同的摆法？
以下图片均为截屏幕截图



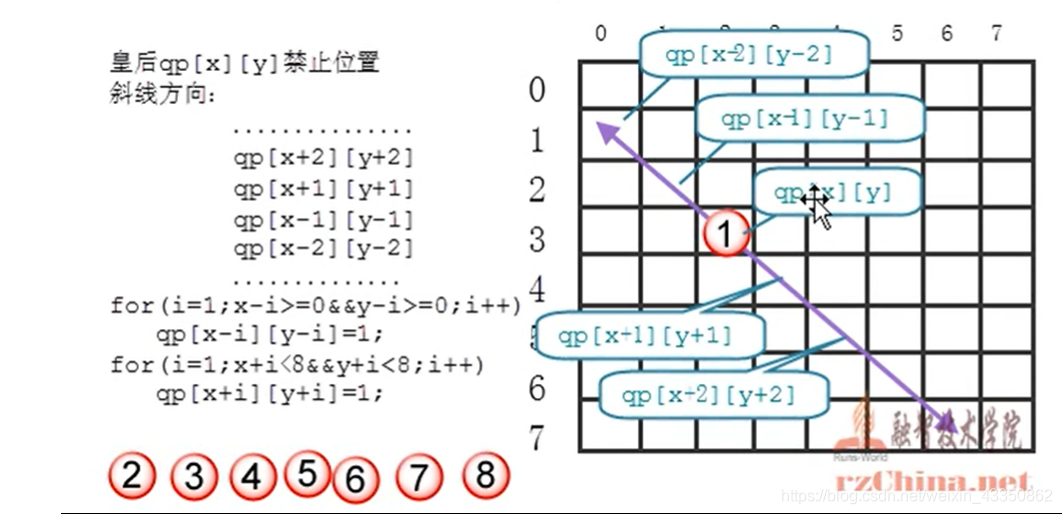
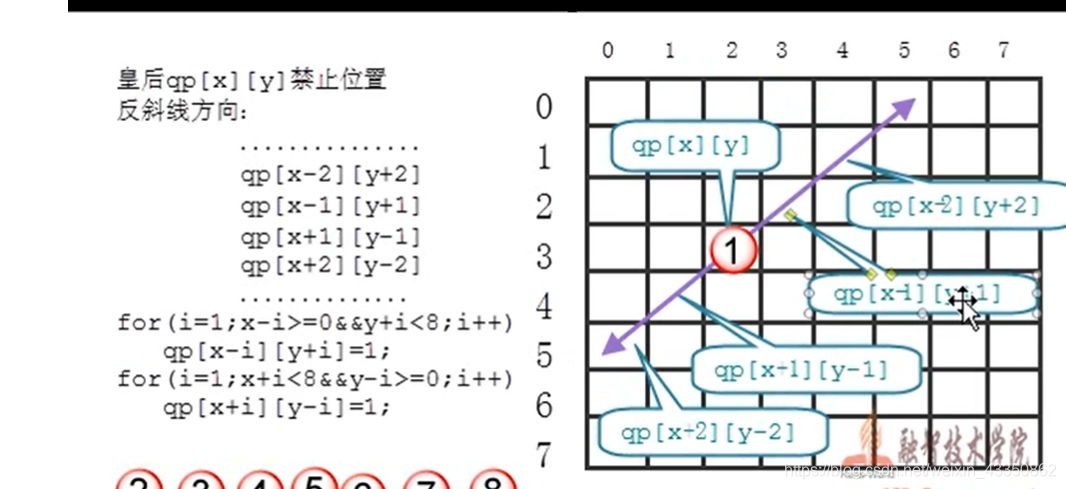
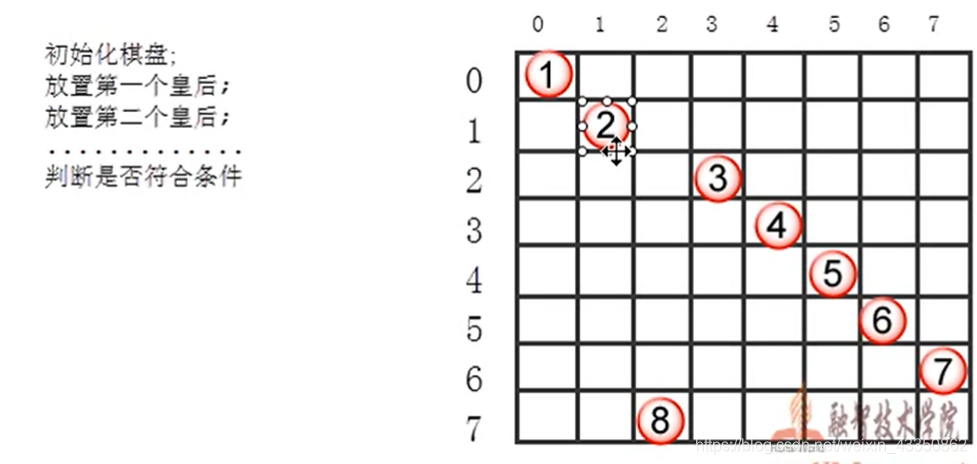
貌似很难，其实很容易想，放置一个，ban位置，再放置第二个，再ban位置，反复操作即可。
一下便是C语言代码：

先写出了打印函数

void exhibition()
{
 int i,j;
 for(i=0;i<8;i++)
 {
  for(j=0;j<8;j++)
  printf("%d",ch[i][j]);
     printf("\n");
 }
 printf("\n");
}

再列出了禁止函数（0为可用空位置；1为ban位；2为可用位置）

void prohibit(int x,int y)
{
 int i,j;
 //放置标记为2，不能放置标记为1；未放置标记为0； 
 //竖排 ch[0][j]~ch[7][y]
 for(i=0;i<8;i++)
 if(i!=x) ch[i][y]=1;
 //横排 ch[i][0]~ch[i][7]
 for(j=0;j<8;j++)
 if(j!=y) ch[x][j]=1;
 //斜线方向禁止位置
 for(i=1;x-i>=0&&y-i>=0;i++)
 ch[x-i][y-i]=1;
 for(i=1;x+i<8&&y+i<8;i++)
 ch[x+i][y+i]=1;
 for(i=1;x-i>=0&&y+i<8;i++)
 ch[x-i][y+i]=1;
 for(i=1;x+i<8&&y-i>=0;i++)
 ch[x+i][y-i]=1;
}

最后为皇后安置代码，（用了简单递归，应该还有可适用更多皇后的递归）：
思想是：安放了第一个皇后之后ban位置，再放置第二个，再ban位置… …直至放置完所有皇后

printf("八皇后问题算法：\n");
 getchar();
 for(queen1=0;queen1<8;queen1++)
  for(queen2=0;queen2<8;queen2++)
   for(queen3=0;queen3<8;queen3++)
    for(queen4=0;queen4<8;queen4++)
     for(queen5=0;queen5<8;queen5++)
      for(queen6=0;queen6<8;queen6++)
       for(queen7=0;queen7<8;queen7++)
        for(queen8=0;queen8<8;queen8++)
        {
             for(i=0;i<8;i++)
             for(j=0;j<8;j++)
             ch[i][j]=0;//初始化
             ch[0][queen1]=2;
             prohibit(0,queen1);
             if(ch[1][queen2]==0)
             {
              ch[1][queen2]=2;
              prohibit(1,queen2);
              if(ch[2][queen3]==0)
              {
               ch[2][queen3]=2;
                  prohibit(2,queen3);
                  if(ch[3][queen4]==0)
                  {
                   ch[3][queen4]=2;
                   prohibit(3,queen4);
                   if(ch[4][queen5]==0)
                   {
                    ch[4][queen5]=2;
                          prohibit(4,queen5);
                          if(ch[5][queen6]==0)
                          {
                           ch[5][queen6]=2;
                              prohibit(5,queen6);
                              if(ch[6][queen7]==0)
                              {
                               ch[6][queen7]=2;
                               prohibit(6,queen7);
                               if(ch[7][queen8]==0)
                                     {
                                   ch[7][queen8]=2;
                                      count++;
                                      printf("第%d种：\n",count);
                                      exhibition();
                         }
         }
        }
       }
      }
     }
    }
     }
 printf("一共有%d种方案。\n",count);

便可执行，代码效果如下图：

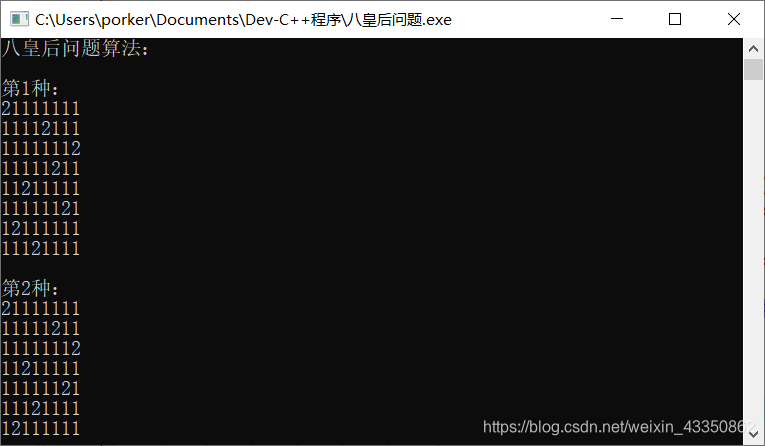
一共92种，是这个答案便代表你已完成本算法。