07、点积与对偶性
以下内容可能与原视频不一致,都是记录我自己的理解,原视频地址 线性代数的本质
点积,定义:内积空间。
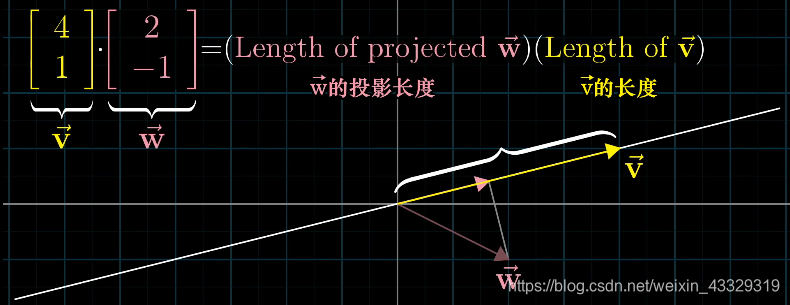
几何意义:
V
⃗
⋅
W
⃗
\vec V·\vec W
V⋅W,是
W
⃗
\vec W
W在
V
⃗
\vec V
V上的投影长度乘以
V
⃗
\vec V
V的长度,这样,有3种情况,
W
⃗
\vec W
W的投影方向与
V
⃗
\vec V
V相同、相反、垂直,对应点积+、-和0。
将其中一个向量例
V
⃗
\vec V
V,看作是一种变成一维的变换(
i
ˉ
\bar i
iˉ和
j
ˉ
\bar j
jˉ都被压缩到一条直线)后的基向量,则点积是此时
W
⃗
\vec W
W变换后的
长度,即坐标和:
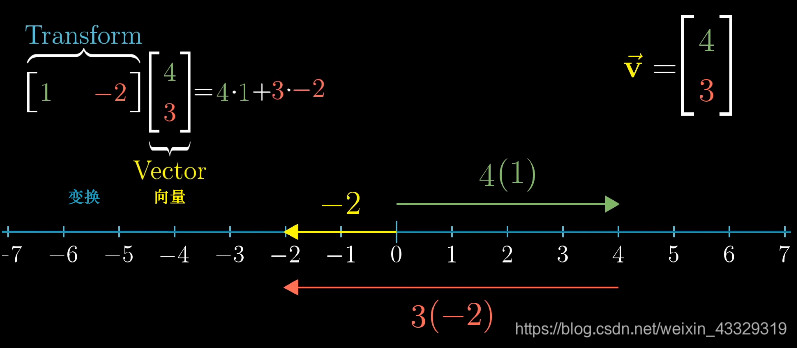
首先简单一点,假定两个值 V ⃗ = [ 1 − 2 ] \vec V=\left[ \begin{matrix}1 \\-2\end{matrix} \right] V=[1−2], W ⃗ = [ 4 3 ] \vec W=\left[ \begin{matrix}4 \\3\end{matrix} \right] W=[43], x x x轴不动, y y y轴倒向 x x x轴, V ⃗ \vec V V是基向量,那么变换矩阵是 [ 1 − 2 0 0 ] \left[ \begin{matrix}1 &-2\\0&0\end{matrix} \right] [10−20]。
W
⃗
\vec W
W变换后的向量为
[
1
−
2
0
0
]
\left[ \begin{matrix}1 &-2\\0&0\end{matrix} \right]
[10−20]
[
4
3
]
\left[ \begin{matrix}4 \\3\end{matrix} \right]
[43],由此可见矩阵乘法与点积的关系互通。
然后,难一点,
x
x
x轴和
y
y
y轴都向着
V
⃗
\vec V
V投影,那么此时变换矩阵是多少呢?也即
i
ˉ
\bar i
iˉ和
j
ˉ
\bar j
jˉ的数值是多少?
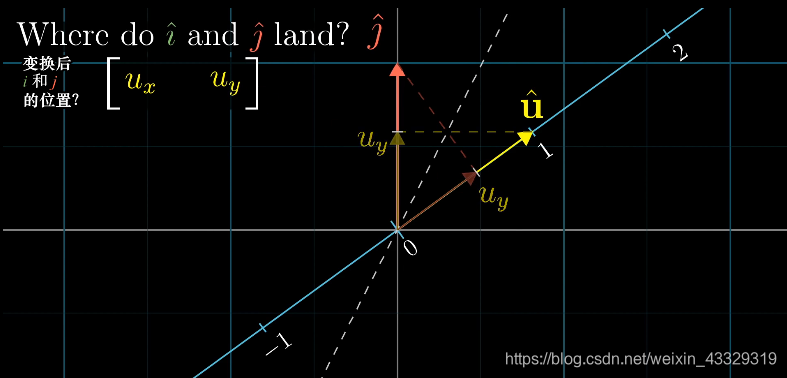
原视频使用对偶性求得。简单假设
V
⃗
\vec V
V为变化后的基向量
u
ˉ
\bar u
uˉ,
j
ˉ
\bar j
jˉ向
u
ˉ
\bar u
uˉ投影等于,
u
ˉ
\bar u
uˉ向
j
ˉ
\bar j
jˉ,
u
ˉ
\bar u
uˉ=
[
u
x
u
y
]
\left[ \begin{matrix}u_x\\u_y\end{matrix} \right]
[uxuy]如下图:
那么转换之后,
[
x
y
]
\left[ \begin{matrix}x \\y\end{matrix} \right]
[xy]的长度就是
u
x
x
+
u
y
y
u_xx+u_yy
uxx+uyy。那么
V
⃗
\vec V
V=
a
u
ˉ
a \bar u
auˉ,也只是加了常数而已。
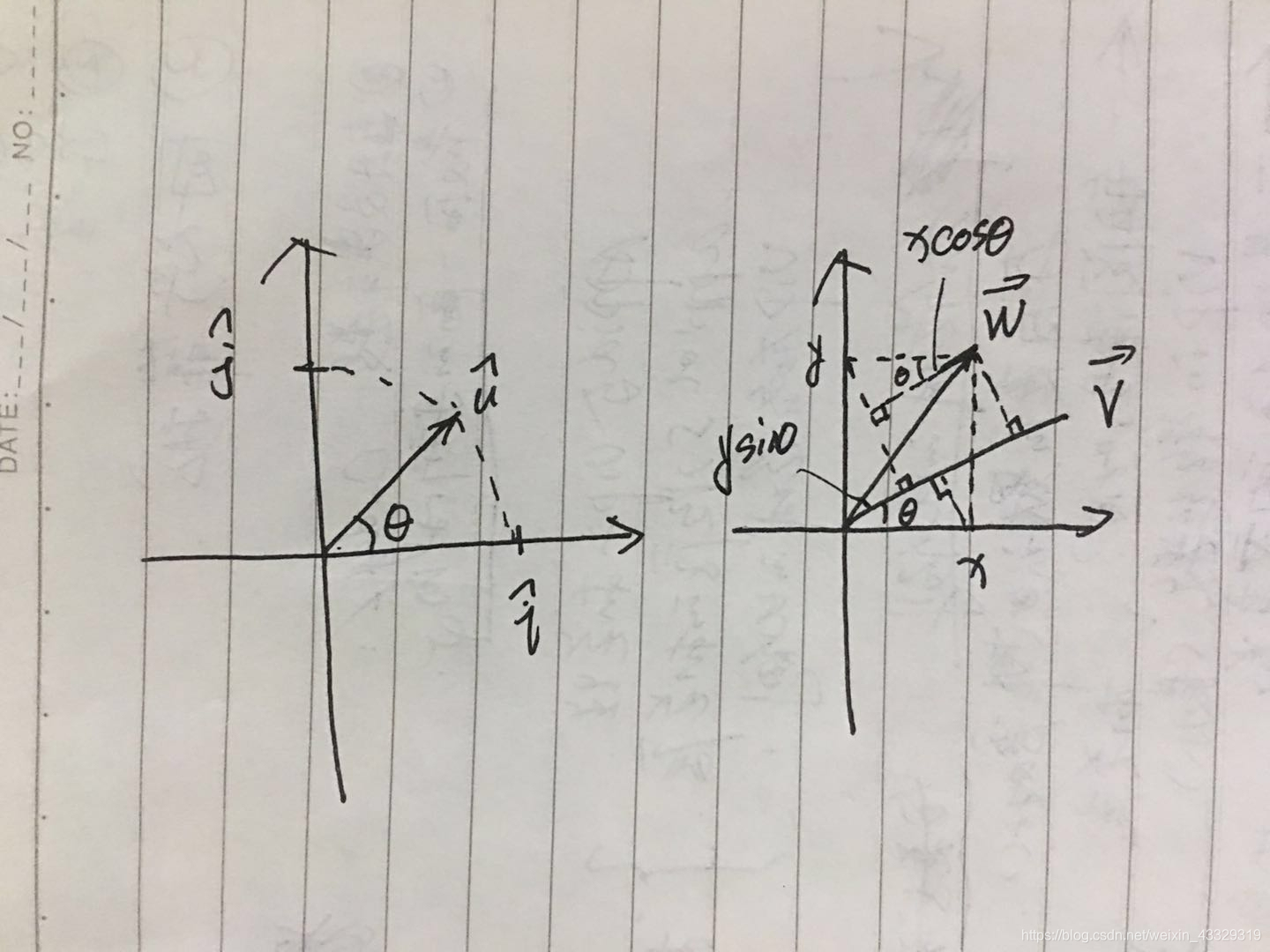
其实,不用对偶性,也可以证明:
如果 u ˉ \bar u uˉ是转换后的唯一基向量,因为长度为1,那么肯定是 [ c o s θ s i n θ ] \left[ \begin{matrix}cos \theta \\sin \theta\end{matrix} \right] [cosθsinθ]对应的角度是 θ \theta θ,那么 W ⃗ \vec W W的对应的坐标 w x , w y w_x,w_y wx,wy在 u ˉ \bar u uˉ的投影分别
是 w x c o s θ , w y s i n θ w_xcos \theta,w_ysin\theta wxcosθ,wysinθ。用三角形知识可以证明 W ⃗ \vec W W在 u ˉ \bar u uˉ的投影是 w x c o s θ + w y s i n θ w_xcos \theta+w_ysin\theta wxcosθ+wysinθ,假设 V ⃗ \vec V V的长度是 a a a。
则 V ⃗ \vec V V· W ⃗ \vec W W的长度= a ( w x c o s θ + w y s i n θ ) a(w_xcos \theta+w_ysin\theta) a(wxcosθ+wysinθ)。转回来,因为 u ˉ \bar u uˉ, V ⃗ = [ a c o s θ a s i n θ ] \vec V=\left[ \begin{matrix}acos \theta \\asin \theta\end{matrix} \right] V=[acosθasinθ],那么点积
V
⃗
\vec V
V·
W
⃗
\vec W
W=
[
a
c
o
s
θ
a
s
i
n
θ
]
\left[ \begin{matrix}acos \theta \\asin \theta\end{matrix} \right]
[acosθasinθ]
[
w
x
w
y
]
\left[ \begin{matrix}w_x \\w_y\end{matrix} \right]
[wxwy]=
a
w
x
c
o
s
θ
+
a
w
y
s
i
n
θ
aw_xcos \theta+aw_ysin\theta
awxcosθ+awysinθ ,看到没,皆大欢喜。附上渣渣手绘图。
08第一部分、叉积的标准介绍
叉积,产生一个新向量,长度等于两个向量的行列式,方向复合右手法则。

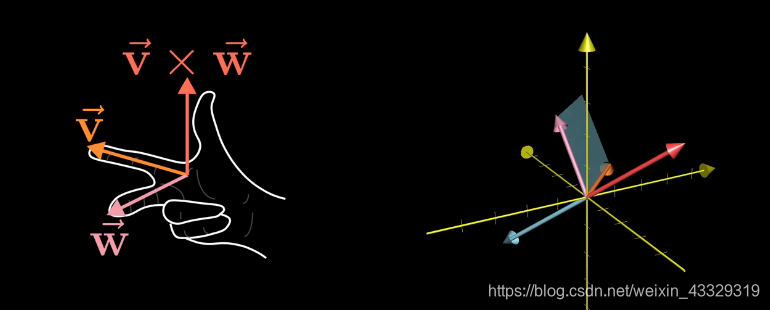
08第二部分、以线性变换的眼光看叉积
叉积的计算,在两个向量前加入一个基向量组,然后计算行列式
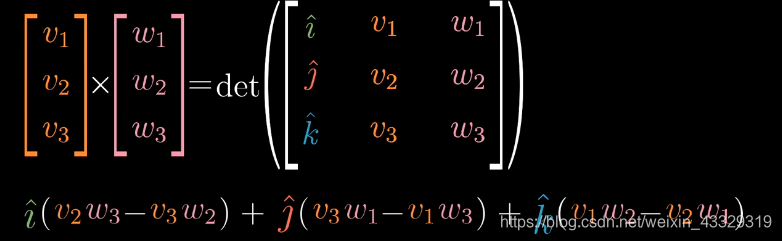
其性质如下:

求证思路如下:

这个过程并不是推理,而是检验,假设存在向量
P
⃗
\vec P
P使基向量组转换成叉积的向量,那么下图的等式就证明叉积的几何意义?
主要证明的是
P
⃗
\vec P
P与由
W
⃗
\vec W
W和
V
⃗
\vec V
V组成的平面垂直,也就是右手法则,这样才能组成行列式的体积!
这个对偶性,没啥好理解的了。









 本文深入探讨了线性代数中点积的几何意义及其与对偶性的关系,并通过实例解释了如何利用点积进行向量的投影运算。此外,还介绍了叉积的概念及其几何解释。
本文深入探讨了线性代数中点积的几何意义及其与对偶性的关系,并通过实例解释了如何利用点积进行向量的投影运算。此外,还介绍了叉积的概念及其几何解释。
















 8062
8062

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








