线性代数的本质1

GiggleMiao

已于 2022-02-04 17:18:32 修改

阅读量1k

点赞数 1

分类专栏：学习笔记线性代数文章标签：线性代数机器学习矩阵

于 2022-02-02 19:04:52 首次发布

本文链接：https://blog.youkuaiyun.com/gigglehuahua/article/details/122768022

版权

学习笔记同时被 2 个专栏收录

13 篇文章

订阅专栏

线性代数

3 篇文章

订阅专栏

干货满满~昨天停更了，因为机器学习白板推导听不明白了。。所以赶紧补补线性代数的课，二刷《线性代数的本质》，内容不难，很有助于打开思维。系列文章会尽量把精华都摘下来，有理解不当处欢迎指出。有兴趣的同学也可以直接去刷视频https://www.bilibili.com/video/BV1ys411472E?p=1http://link

向量究竟是什么？

在线性代数中，最基础最根源的组成部分就是向量，向量的加法和向量的乘法贯穿线性代数始终。而向量的定义，主要有三种角度的说法：

1）物理视角——向量是空间中的箭头，只要确定了它的长度和方向不变，就可以任意移动该向量而保持不变。

2）计算机视角——向量是有序的数字列表，在解决具体问题时选取不同的特征作为列表进行计算。

3）数学角度（抽象）——只要保证两个向量相加以及数字与向量相乘有意义，向量可以是任何东西。

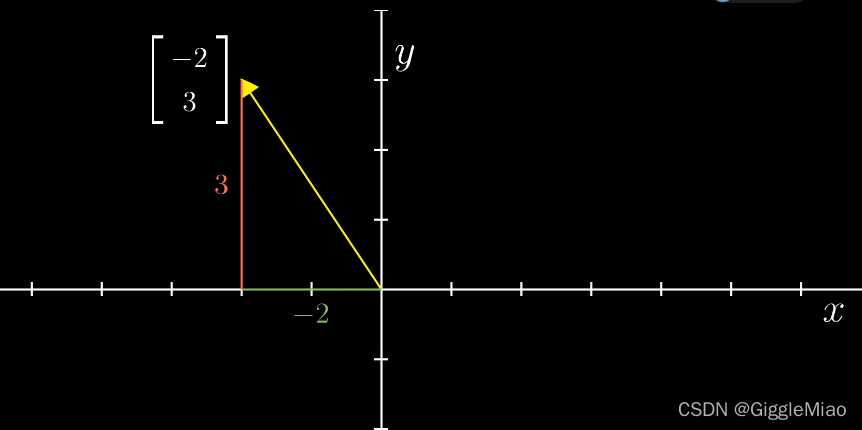
在“向量是有序的数字列表”中，如上图中黄色箭头表示的向量，第一个数告诉你从原点处沿着x轴走了多远，第二个数告诉你在此基础上沿着平行于y轴的方向走了多少。其中正数代表向右移动，负数代表向左移动。并且在线性代数中，一般默认向量的起源在原点。并且为了和坐标中的点(-2,3)进行区分，通常竖着写来表示向量 $\begin{bmatrix} -2\\ 3 \end{bmatrix}$ 。

每一对这样的数 $\begin{bmatrix} x\\ y \end{bmatrix}$ 给出唯一一个向量，每一个向量恰好对应唯一一对数 $\begin{bmatrix} x\\ y \end{bmatrix}$ 。

向量的加法 $\vec{v}+\vec{w}$ ：

1）平移其中一个向量，使它的起点与另一个向量的终点重合：

2）然后从固定不动的向量起点出发，指向第平移向量的终点，此时构成的新向量就是 $\vec{v}+\vec{w}$ 的和。：

3）从“计算”的角度认为向量加法就是把对应项相加：

向量的数乘 $k\vec{v}$ ：

向量乘以一个数k，即是对向量进行拉伸和压缩k倍，-k时进行反向。也可以说，数字在线性代数中起到的主要作用就是缩放向量。（线性代数中，“数字”和“标量”认为是一样的）

从“计算”的角度认为向量与标量（数字）相乘就是将向量中的每个分量与标量相乘。

我们看到的每一个点，其实都可以认为是以该点为终点，原点为起点的一个向量。

线性组合、张成的空间与基

基

每当我们用数字描述向量时，它都依赖于我们正在使用的基。上述所说的向量可以认为是对一对基向量进行“缩放之后并相加”得到的，也可以说是基向量的线性组合。

一般情况下，默认指向x轴正向和y轴正向且单位为1的向量作为标准基。

当把坐标看作标量时，使用这些标量对基向量进行缩放相加，可以得到一个新的二维向量。如坐标（3，-2）作用于基向量 $\begin{bmatrix} \hat{i}\\ \hat{j} \end{bmatrix}$ ——即把 $\hat{i}$ 向量拉伸为原来的3倍， $\hat{j}$ 向量拉伸为原来的2倍并反向，得到了新的向量 $\begin{bmatrix} 3\\ -2 \end{bmatrix}$ 。

思考：如果选择不同的基向量会怎样？

在二维空间中，随便选择一对相互垂直的向量作为基向量，然后任意选择两个坐标标量，分别用于缩放这一对基向量，把结果相加，也会得到二维空间中的一个新向量。

张成的空间

上面我们反复提到对基进行“缩放向量并相加”，就是一种线性组合，所有可以表示为给定向量线性组合的向量的集合，被称为给定向量张成的空间（SPAN）。

· 在二维空间中，如果不断改变坐标标量的值对一对基向量进行“缩放向量并相加”（做加法才是这个二维基下对应的向量 $\vec{x}=\begin{bmatrix} a\\ b \end{bmatrix}=a\hat{i}+b\hat{j}$ ，不做加法的话只是两个缩放了的基向量），可以表示出所有的线性组合 $a\vec{v}+b\vec{w}$ ，即整个二维空间。

进一步讨论：

1）若两个基向量共线时，，产生的所有向量会被限制在一条直线上。

2）当两个基向量都是零向量时，则产生的向量都是零向量。

· 在三维空间中，如果不断改变坐标标量的值对一组相互垂直的三维基向量进行“缩放向量并相加”，可以表示出所有的线性组合 $a\vec{v}+b\vec{w}+c\vec{u}$ ，即整个三维空间。

进一步讨论：

如果第三个基向量恰好落在另外两个向量所张成的二维空间中（三个向量并不垂直），此时三个向量能够张成的空间并不改变。也可以理解为这一组向量中至少有一个是多余的基向量，没有对张成空间做出任何贡献。这种情况下，称这三个向量之间线性相关。其中的任何一个向量都可以表示为其他向量的线性组合：

如果所有的向量都给张成的空间增添了新的维度，则称这些向量之间是线性无关的：

由以上内容，可以将向量空间中的一组基定义为是张成该空间的一个线性无关的向量集。

思考：看了这个视频明白了不是方阵的矩阵A的秩 $R(A)\leq min\left \{ m,n \right \}$ 。比如三行四列的矩阵，三维空间用四个向量表示，肯定用不完啊，肯定存在列线性相关；四行三列的矩阵，三个向量放到四维空间中，也绝对够用啊，肯定存在行线性相关。

矩阵与线性变换

矩阵

线性代数当中的矩阵，可以解读为对空间的一种特定变换。如一个二维的线性变换仅由四个数字进行确定，标准基 $\hat{i}$ 变换后的基对应的二维坐标和标准基 $\hat{j}$ 变换后的基对应的二维坐标。通常把这些坐标包装在一个 $2\times 2$ 的格子里，称为 $2\times 2$ 矩阵：

当我们看到一个矩阵时，就要想到它的每一列都是经过变换后的基向量。

线性变换

线性变换是操纵空间的一种手段，“变换”表示可以可视化的呈现向量在空间上的变化。当满足以下两点时，称为是线性的变换：1）直线在变换后仍然保持为直线，不能有所弯曲；2）原点保持固定。

当一个向量进行线性变换时，可以理解为该向量在标准基进行该线性变换后的基上的表示结果。展开来说就是先对基进行线性变换，然后该向量在变换后的基上的表示，即为此向量进行线性变换的结果。

上段话说的有点绕，让我们来举个“栗子”：

· 如果想把一个向量 $\begin{bmatrix} x\\ y \end{bmatrix}$ 进行逆时针旋转90°的变换，则可以先把该基进行逆时针90°变换，然后让向量坐标作用在变换之后的基上就可以了。

逆时针旋转90°

$\hat{i}=\begin{bmatrix} 1\\ 0 \end{bmatrix}\rightarrow \begin{bmatrix} 0\\ 1 \end{bmatrix}$ ， $\hat{j}=\begin{bmatrix} 0\\ 1 \end{bmatrix}\rightarrow \begin{bmatrix} -1\\ 0 \end{bmatrix}$ 。变换后的基组合为 $\begin{bmatrix} 0 &-1 \\ 1&0 \end{bmatrix}$ （每列对应一个变换后的基向量坐标）。

然后将该向量表示在变换后的基上 $x\begin{bmatrix} 0\\ 1 \end{bmatrix}+y\begin{bmatrix} -1\\ 0 \end{bmatrix}$ ，即为该向量进行了逆时针90°的旋转变换。

矩阵·向量

向量在变换后的基上的表示形式 $x\begin{bmatrix} 0\\ 1 \end{bmatrix}+y\begin{bmatrix} -1\\ 0 \end{bmatrix}$ 实际上就是矩阵与向量之间做乘法 $\begin{bmatrix} 0 & -1\\ 1& 0 \end{bmatrix}\begin{bmatrix} x\\ y \end{bmatrix}$ 的计算过程。观察线性变换对一个向量的作用，只需要取出向量的坐标，将它们分别与变换后的基矩阵进行相乘即可，其中矩阵的每一列对应一个变换后的基向量：

矩阵乘法中的左右顺序不能随意颠倒，基在左侧坐标在右侧，可以读作——在基 $\begin{bmatrix} a & c\\ b & d \end{bmatrix}$ 下坐标为 $\begin{bmatrix} x\\ y \end{bmatrix}$ 的向量是 $x\begin{bmatrix} a\\ c \end{bmatrix}+y\begin{bmatrix} b\\ d \end{bmatrix}$ （跟“缩放基向量并求和”一样意思）。说明了矩阵与向量的乘法计算相当于是向量在变换后的基下的线性组合。

矩阵乘法与线性复合变换

前面我们说了矩阵与向量的乘法，接下来讨论矩阵与矩阵的乘法。依然是从几何意义进行入手。

以二维为例，当基 $\begin{bmatrix} x\\ y \end{bmatrix}$ 经过了一组线性变换M1后又经过了一次线性变换M2，此时称对基 $\begin{bmatrix} x\\ y \end{bmatrix}$ 进行了复合变换。效果如下：

看的时候要从右往左读——基 $\begin{bmatrix} x\\ y \end{bmatrix}$ 先进行了 $\begin{bmatrix} 0 & -1\\ 1& 0 \end{bmatrix}$ 的变换，在此基础上又进行了 $\begin{bmatrix} 1 &1 \\ 0& 1 \end{bmatrix}$ 的变换。这种复合变换的结果，也就是我们所说的矩阵的乘法运算。

结论——矩阵相乘的结果也就是标准基进行复合变换的结果。

· 举个例子来详细说明矩阵相乘的几何意义。假设标准基先经过M1 $\begin{bmatrix} 1 &-2 \\ 1 & 0 \end{bmatrix}$ 的变换，得到了变换后的基矩阵为 $\begin{bmatrix} 1 &-2 \\ 1 & 0 \end{bmatrix}$ ，然后又经过M2 $\begin{bmatrix} 0 & 2\\ 1 & 0 \end{bmatrix}$ 的变换，这相当于在基变换成

$\begin{bmatrix} 1 &-2 \\ 1 & 0 \end{bmatrix}$ 之后，其中每一列向量 $\begin{bmatrix} 1\\1 \end{bmatrix}$ ， $\begin{bmatrix} -2\\ 0 \end{bmatrix}$ 又都经过了M2 $\begin{bmatrix} 0 & 2\\ 1 & 0 \end{bmatrix}$ 的变换的结果。分步：

1）标准基 $\begin{bmatrix} \hat{i}\\ \hat{j} \end{bmatrix}$ 经过M1变换后变成了 $\begin{bmatrix} 1 &-2 \\ 1 & 0 \end{bmatrix}$ 。

2）1）中列向量 $\begin{bmatrix} 1\\1 \end{bmatrix}$ 经历了M2 $\begin{bmatrix} 0 & 2\\ 1 & 0 \end{bmatrix}$ 变换，相当于矩阵和向量的乘积 $\begin{bmatrix} 0 & 2\\ 1 & 0 \end{bmatrix}$ $\begin{bmatrix} 1\\1 \end{bmatrix}$ ，为 $\hat{i}$ 经复合变换后的结果，即复合矩阵中的第一列。

3） 1）中列向量 $\begin{bmatrix} -2\\ 0 \end{bmatrix}$ 经历了M2 $\begin{bmatrix} 0 & 2\\ 1 & 0 \end{bmatrix}$ 变换，相当于矩阵和向量的乘积 $\begin{bmatrix} 0 & 2\\ 1 & 0 \end{bmatrix}$ $\begin{bmatrix} -2\\ 0 \end{bmatrix}$ ，为 $\hat{j}$ 经复合变换后的结果，即复合矩阵中的第二列。

矩阵相乘的交换和结合

矩阵相乘不能交换的原因时先经过M1变换再经过M2变换，与基先经过M2变换再经过M1变换的结果不一样。

而结合律有效的原因是无论怎么变化小括号的位置，从右往左的变换顺序都是固定的，不影响复合变换的结果。

思考：看完这节视频我明白了为什么矩阵相乘时左边矩阵的列数与右边矩阵的行数相等。从变换的角度从右往左看的话是右边矩阵的每一列向量需要进行左边矩阵所表示的变换，而向量坐标数和基数是相互对应的，即n维的向量要在n维的基上进行表示。