07、极限
因为之前的内容,都是直观性的讲解,所以本节是要准确的给出3个定义:

G1、导数的正式定义
下面写法等价, d f d x ( 2 ) = lim x → 0 f ( 2 + h ) − f ( 2 ) h \frac{df}{dx}(2)= \lim _{x \to 0 }\frac{f(2+h)-f(2)}{h} dxdf(2)=limx→0hf(2+h)−f(2)
导数指函数 f f f,当 d x dx dx逼近于0时, f f f逼近于某个值时(上例为2)的变化,(不是 d x dx dx取无穷小)
主要注意,
d
x
dx
dx本身包含逼近于零时的含义,而
h
h
h的写法则需要明确这件事。
G2、极限的定义
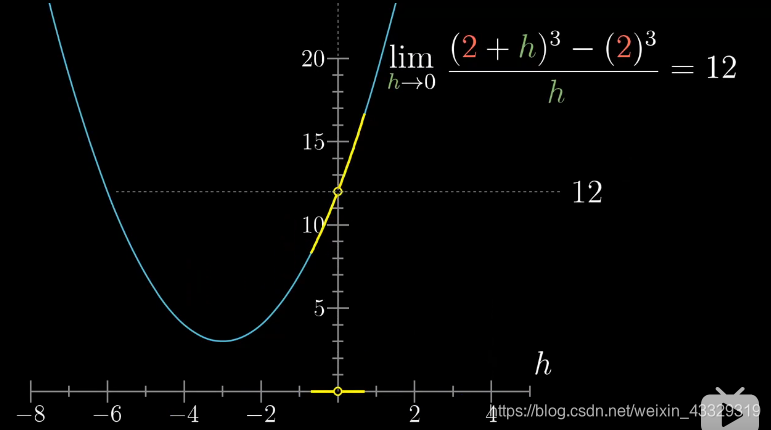
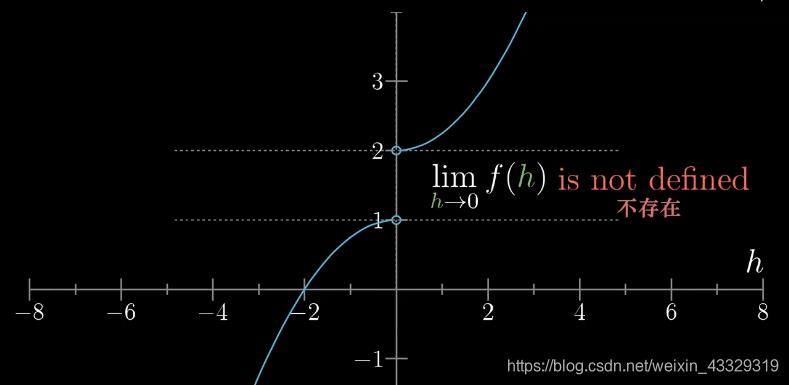
考虑上面两张图的函数,都在0点位置断点,因为当
h
=
0
h=0
h=0,分母为0,但是下面的函数不存在极限
lim
h
→
0
f
(
h
)
\lim_{h \to 0} f(h)
limh→0f(h)
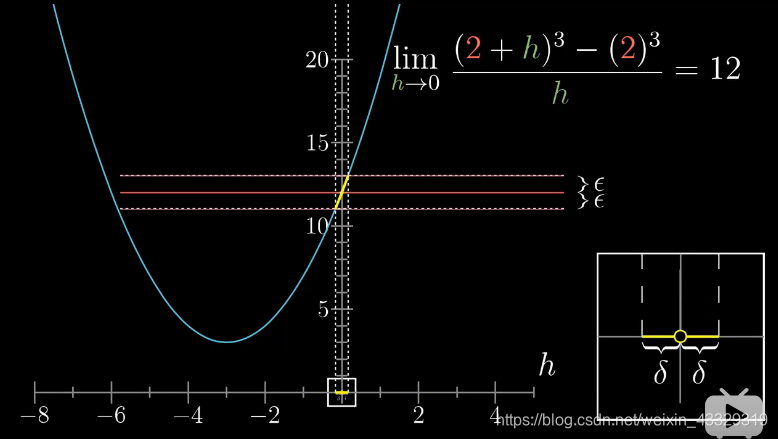
因为第一个函数在函数断点处,两侧取一个范围 δ \delta δ,对应会有一个函数值的范围 ϵ \epsilon ϵ,在此范围内, δ \delta δ和
ϵ \epsilon ϵ,一一对应。
而第二个函数则不能。
G3、洛必达法则
如下图函数,由于 f ( a ) = 0 , g ( a ) = 0 f(a)=0,g(a)=0 f(a)=0,g(a)=0,所以在a点无法计算,他们的商。
可以采用,极限的方式:
lim
x
→
a
f
(
x
)
g
(
x
)
\lim_{x \to a}\frac{f(x)}{g(x)}
limx→ag(x)f(x),对其分别求极限值,然后求商,如下图:
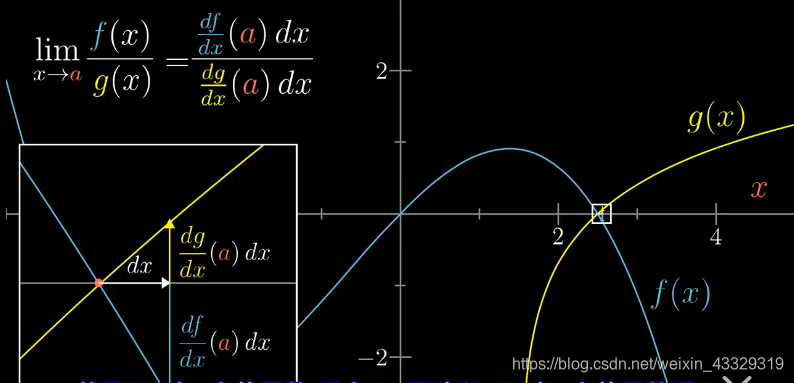
实际上,因为,两个无穷小之比或两个无穷大之比的极限可能存在,也可能不存在。洛必达法则,就是用来求这个值的。
除了零比零形式,还有无穷比无穷 ,基本形式。洛必达法则
08、积分和微积分基本定理
正式定义:牛顿-莱布尼茨公式的内容是一个连续函数在区间 [ a,b ] 上的定积分等于它的任意一个原函数在区间[ a,b ]上的增量。牛顿-莱布尼茨公式
本节只是形象的解析这个公式:求导与积分,为互逆运算
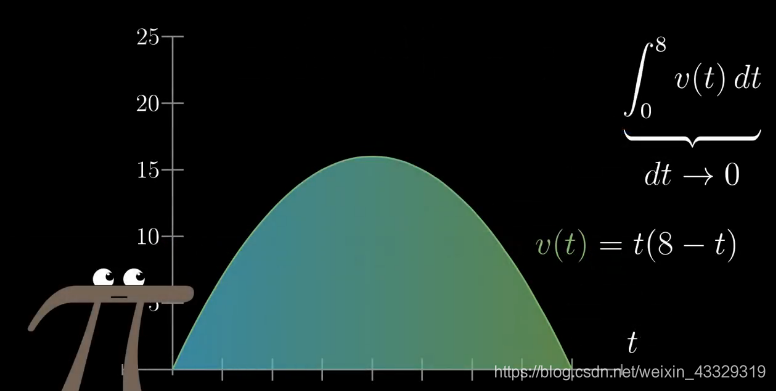
如下图,车辆的形式速度的曲线,其下方的面积就是其积分(即原函数)
例如 v ( t ) = t ( 8 − t ) v(t)=t(8-t) v(t)=t(8−t),其原函数有多个,但是在[0,8]区间积分,有唯一值 ∫ 0 8 v ( t ) d t \int_0^8v(t)dt ∫08v(t)dt
需要注意,如果图像在x轴下方,则为负值。
09、面积和斜率有什么关系?
如下图,如何求
s
i
n
(
x
)
sin(x)
sin(x)在
[
0
,
π
]
[0,\pi]
[0,π]之间的平均值?
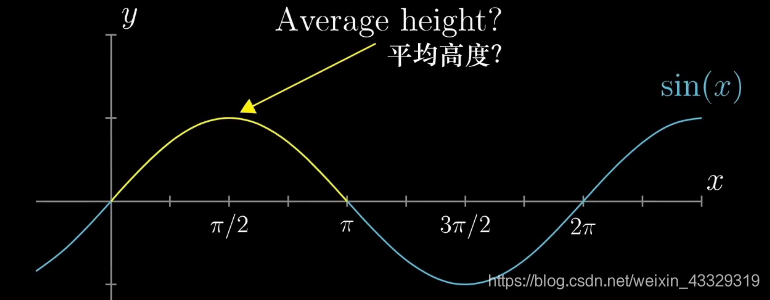
毫无疑问,求面积除与长度。求面积就需要,原函数。
s
i
n
(
x
)
sin(x)
sin(x)的原函数是
−
c
o
s
(
x
)
-cos(x)
−cos(x),从下图可见,求出来的值,应该是原函数在两点之间的斜率!
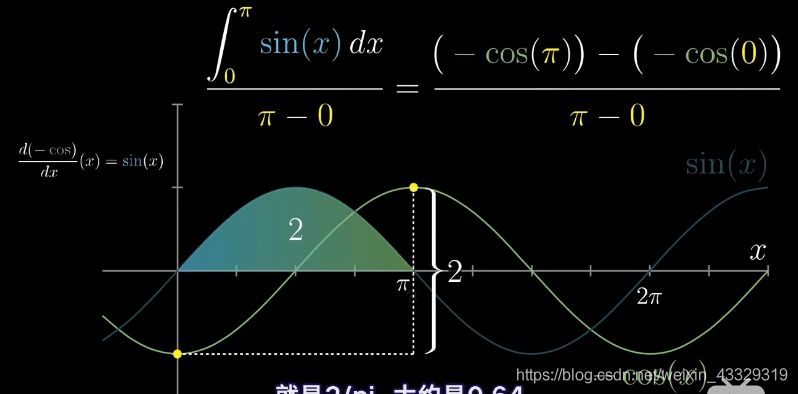
这个也好解析:斜率是
Δ
y
Δ
x
\frac{\Delta y}{\Delta x}
ΔxΔy,斜率在两点之间的平均,就是两点之间的累积和之比。








 本文深入浅出地介绍了微积分中的核心概念,包括导数、极限、洛必达法则及其应用,详细解析了积分与微积分基本定理,并探讨了面积与斜率之间的内在联系。
本文深入浅出地介绍了微积分中的核心概念,包括导数、极限、洛必达法则及其应用,详细解析了积分与微积分基本定理,并探讨了面积与斜率之间的内在联系。
















 457
457

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








