hdu5015 233Matrix(矩阵快速幂+思维）好题

https://vjudge.net/problem/HDU-5015
这题是一道2014icpc区域赛的题果然就是有难度，而且想法确实不错，这题的地推矩阵真的不好想，也是看了大佬的博客才理解的，总结了一点经验，算是学到了一点东西，锻炼了一下思维能力，：
参考了大佬的解题思路：
因为数据量很大，暴力求解肯定是不行的。必定超时，虽然给定的时间是5秒钟。
那接下来就是推公式了，而我最终也真的推出来个公式，但很遗憾，它只有当n和m相等的时候才成立，可是n最大才为10，这种思路也就被否定了。
既然给定的是一个矩阵的形式，难道可以用矩阵快速幂搞出来？可以试试。注意一点，如果能构造出来快速幂的话，也只有按列来推。
因为a[0][1]=233，a[0][2]=2333，a[0][3]=23333，…………，所以有a[0][i]=10*a[0][i-1]+3（i>1，a[0][1]=233）

如果令a[0][0]=23，那么a[0][i]=10*a[0][i-1]+3（i>0，a[0][0]=23）

则对于n+1行，m+1列的矩阵A，有
第一列，下标j = 0

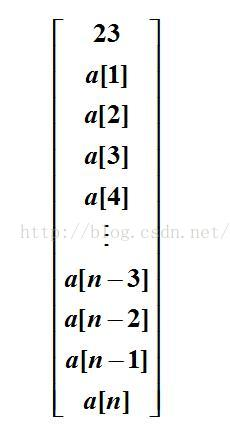
第二列：

第三列：

对上述矩阵的各列适当变形得：

第一列（下标j=0）

第二列（下标j=1）:


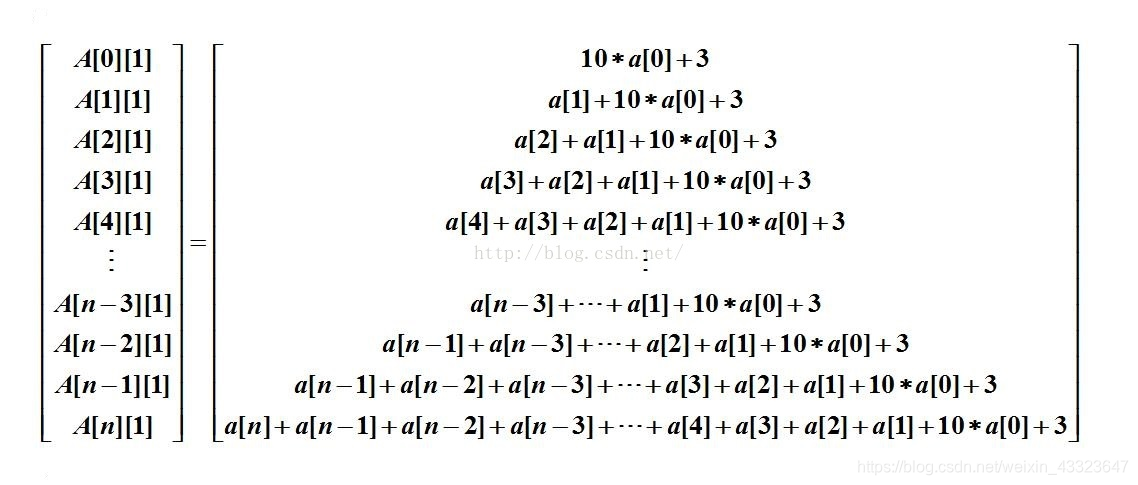
所以得出地推矩阵就是：

=
这是AC代码:

#include <iostream>
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod = 1e7 + 7;
int n,m;
ll a[15];
struct matrix{
    ll a[15][15];
    matrix()
    {
        memset(a,0,sizeof(a));
    }
};
matrix Matrix(matrix a,matrix b)
{
    matrix c;
    for(int i = 1;i <= n + 2;i++)
    {
        for(int j = 1;j <= n + 2;j++)
        {
            for(int k = 1;k <= n + 2;k++)
            {
                c.a[i][k] = (c.a[i][k] + a.a[i][j] * b.a[j][k]) % mod;
            }
        }
    }
    return c;
}
matrix quick_pow(matrix A,ll x)
{
    matrix ans;
    for(int i = 1;i <= n + 2;i++)
    {
        ans.a[i][i] = 1;
    }
    while(x)
    {
        if(x&1)
        {
            ans = Matrix(ans,A);
        }
        A = Matrix(A,A);
        x/=2;
    }
    return ans;
}
int main()
{
    while(scanf("%d%d",&n,&m) != EOF)
    {
       matrix A,B;
       A.a[1][1] = 23;
       for(int i = 1;i <= n;i++)
       {
           scanf("%lld",&A.a[i+1][1]);
       }
       A.a[n+2][1] = 3;
       for (int i = 1; i <= n + 1; i++)
			B.a[i][1] = 10;
		for (int i = 1; i <= n + 2; i++)
			B.a[i][n + 2] = 1;
		for (int i = 1; i < n + 2; i++)
			for (int j = 2; j <= i; j++)
				B.a[i][j] = 1;
        B = quick_pow(B,m);//这是地推矩阵
        A = Matrix(B,A);//这是最后称出来的的那个矩阵
        cout << A.a[n+1][1]%mod << endl;
    }
}