二叉搜索树

• 树

线性结构中结点具有唯一前驱和唯一后继的关系，而非线性结构中结点间前驱、后继的关系并不具有唯一性。在树结构中，结点间关系是前驱唯一而后继不唯一，即树结构中结点间是一对多的关系；图结构中结点间是多对多的关系。
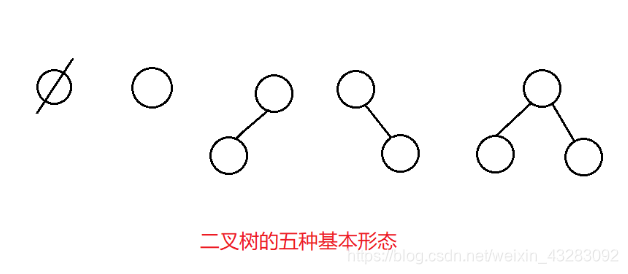
1、 树：元素与元素之间存在一对多的关系 层次关系
2、根节点 叶子结点 孩子结点 父亲结点 （双亲结点）兄弟结点 堂兄弟 祖先结点 子孙结点 前辈 后辈

• 二叉树

二叉树：每个结点的度都不大于2；
没个节点的孩子结点次序不能任意颠倒

3. 二叉树：就是一种特殊的树结构 元素节点最多有两个孩子节点
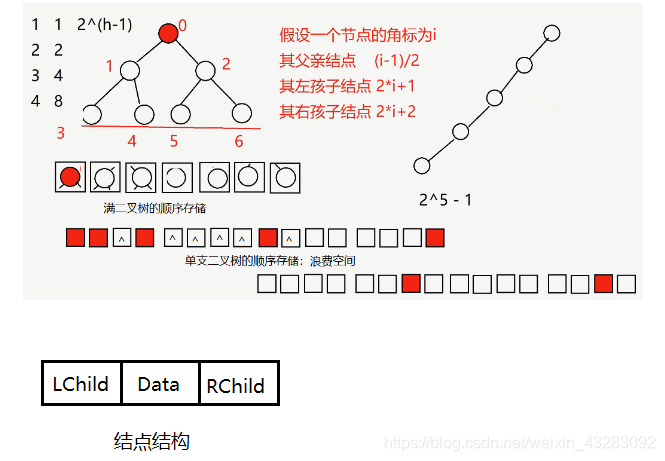
   4.二叉树怎么存？动态数组 动态链表
   5.如果用动态数组存一个深度为h的二叉树 最多需要 2^h-1
   6.每一层最多几个节点 2^(h-1)
   如果此时的二叉树不是一个平衡二叉树 那么用动态数组存会有很多空间浪费
   平衡二叉树：满二叉树和完全二叉树
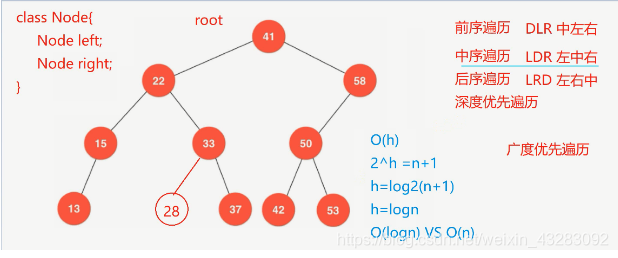
   7.满二叉树：叶子节点的深度差为0 且最后一层全是叶子结点
4. 完全二叉树：是按照每一层从左到右填充节点，叶子节点的深度差<=1
5. 满二叉树一定是完全二叉树
   完全二叉树不一定是满二叉树
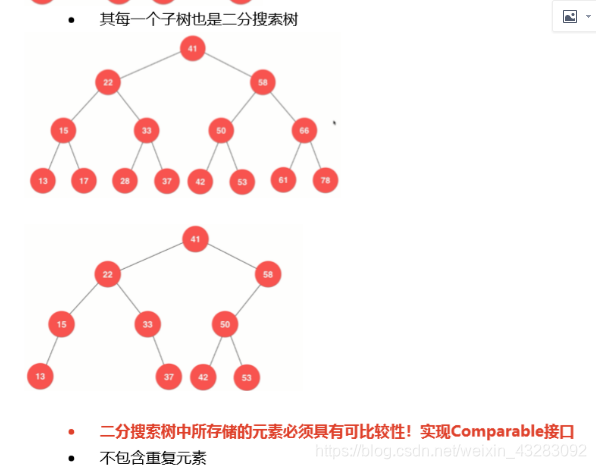
   10.二分搜索树：就是一颗二叉树,只不过有一些条件限定
   目前这个二分搜索树是非平衡！（平衡二叉树：AVL和红黑树）
   二叉搜索树又叫 二叉排序树或二叉顺序树
   对于二叉树中的每一个结点
   其左子树中所有的结点都小于该节点
   其右子树中所有的结点都大于该节点
   相等怎么处理？不对相等做处理！不能存储重复元素
   
   目前为止 关于O(logn) 二分查找 插入排序 二分搜索树 快速排序

package org.yanan.二分搜索树;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;

public class BinarySearchTree<E extends Comparable<E>> {//用二分搜索树存储的元素必须具有可比较性
	//1.定义内部类，结点
	private class Node{
		public E e;
		public Node left,right;
		//内部类的构造函数
		public Node(E e){
			this.e=e;
			left=null;
			right=null;
		}
	}
	//2.定义成员变量
	private Node root;
	private int size;
	//3.定义构造函数
	public BinarySearchTree(){
		root=null;//根节点，不是虚拟头结点
		size=0;
	} 
	//4.获取树中元素个数
	public int size(){
		return size;
	}
	//5.判断树是否为空
	public boolean isEmpty(){
		return size()==0;
	}
	//6.添加元素
	public void add(E e){//添加的元素首先和根作比较，大于超右子树走，小于超左子树走
		root=add(root,e);//如果此时是一颗空树，插入的结点为根节点
		//迭代实现添加
		/*
		 if(size==0){
		 	root=new Node(e);
		 	size++;
		 }
		 Node p=root;
		 while(true){
		 	if(e.compareTo(p.e)==0){
		 		return;
		 	}else if(e.compareTo(p.e)>0){
		 		if(p.right!=null){
		 			p=p.right;
		 		}else{
		 			p.right=new Node(e);
		 			size++;
		 			return;
		 		}
		 	}else if(e.compareTo(p.e)<0){
		 		if(p.left!=null){
		 			p=p.left;
		 		}else{
		 			p.left=new Node(e);
		 			size++;
		 			return;
		 		}
		 	}
		 }
		  */
	}
	//递归,当传入的节点遍历到叶结点之下（即：node==null）或者在空树中传入一个结点，此节点就为根节点
	//以node为当前树的根节点，添加元素e并返回该树的根
	private Node add(Node node, E e) {
		//递归出口
		if(node==null){
			size++;
			return new Node(e);
		}
		if(e.compareTo(node.e)<0){
			node.left=add(node.left,e);
		}else if(e.compareTo(node.e)>0){
			node.right=add(node.right,e);//将整个结点的右子树重新给node.right，重新拼接上
		}
		return node;
	}
	//7.查询元素，查找元素e是否存在于二分搜索树中
	public boolean contains(E e){
		return contains(root,e);
		//迭代实现查找
		/*
		 if(size==0){
		 	return false;
		 }
		 Node p=root;
		 while(p!=null){
		 	if(e.compareTo(p.e)>0){
		 		p=p.right;
		 	}else if(e.compareTo(p.e)<0){
		 		p=p.left;
		 	}else{
		 		return true;
		 	}
		 }
		 return false;
		*/
	}
	//递归：查找以node为根结点的树中是否包含元素e
	private boolean contains(Node node, E e) {
		//递归出口
		if(node==null){//如果找到树的叶子结点的下一层了，即node==null,找不到
			return false;
		}
		if(e.compareTo(node.e)<0){
			return contains(node.left,e);
		}else if(e.compareTo(node.e)>0){
			return contains(node.right,e);
		}else{
			return true;
		}
	}
	//8.前序遍历，根左右，深度优先遍历
	public void preOrder(){
		preOrder(root);
	}
	private void preOrder(BinarySearchTree<E>.Node node) {
		//前序遍历
		if(node==null){
			return;
		}
		System.out.println(node.e);
		preOrder(node.left);
		preOrder(node.right);
	}
	//9.中序遍历，左根右，深度优先
	public void inOrder(){
		ArrayList<E> list=new ArrayList<>();
		inOrder(root,list);
		System.out.println(list);
	}
	private void inOrder(Node node, ArrayList<E> list) {
		//递归：中序遍历root为根的树，并将结果放入list集合中
		if(node==null){
			return;
		}
		inOrder(node.left,list);
		list.add(node.e);
		inOrder(node.right,list);
	}
	//10.后序遍历，左右根，深度优先
	public void postOrder(){
		postOrder(root);
	}
	private void postOrder(BinarySearchTree<E>.Node node) {
		if(node==null){
			return;
		}
		postOrder(node.left);
		postOrder(node.right);
		System.out.println(node.e);
	}
	//11.层序遍历，广度优先,按照层次走:利用队列，根节点入队，然后出队，只要结点出队，再将结点的左右孩子入队 
	public void levelOrder(){
		Queue<Node> queue=new LinkedList<>();
		ArrayList<E> list=new ArrayList<E>();
		queue.add(root);//将根节点入队
		while(!queue.isEmpty()){
			Node current=queue.poll();//将队列中的第一个元素弹出
			list.add(current.e);//放入list集合中
			if(current.left!=null){
				queue.add(current.left);
			}
			if(current.right!=null){
				queue.add(current.right);
			}
		}
		System.out.println(list);//打印list，此时list中存放的就是层序遍历的结果
	}
	//12.获取最小值
	public E minimum(){
		if(size==0){
			throw new IllegalArgumentException("Tree is empty");
		}
		return minimum(root).e;
	}
	private Node minimum(BinarySearchTree<E>.Node node) {
		if(node.left==null){//从根开始，一直遍历树的的左子树，若某一结点没有左子树，那该节点是最小的
			return node;
		}
		return minimum(node.left);
	}
	//13.获取最大值
	public E maximum(){
		if(size==0){
			throw new IllegalArgumentException("Tree is empty");
		}
		return maximum(root).e;
	}
	private Node maximum(BinarySearchTree<E>.Node node) {
		if(node.right==null){
			return node;
		}
		return maximum(node.right);
	}
	//14.删除最小值:改动树(增或删)后，返回新树的根节点，删除数的最小值并返回新树的根
	public E removeMin(){
		E e=minimum();
		root=removeMin(root);
		return e;
	}
	private Node removeMin(Node node) {
		if(node.left==null){
			Node nodeLeft=node.right;//把最小值的右子树给其父节点做左子树
			node.right=null;//切断关系
			size--;
			return nodeLeft;
		}
		node.left=removeMin(node.left);
		return node;
	}
	//15.删除最大值：以node为根节点，删除二叉排序树的最大值并返回新树的根
	public E removeMax(){
		E e=maximum();
		root=removeMax(root);
		return e;
	}
	private Node removeMax(Node node) {
		if(node.right==null){
			Node nodeRight=node.left;
			node.left=null;
			size--;
			return nodeRight;
		}
		node.right=removeMax(node.right);
		return node;
	}
	//16.删除任意值:以root为根删除指定元素后返回新树的根
	public void remove(E e){
		root=remove(root,e);
	}
	private Node remove(Node node, E e) {
		if(node==null){
			return null;
		}
		if(e.compareTo(node.e)>0){
			node.right=remove(node.right,e);
			return node;//未找到，递归继续，
		}else if(e.compareTo(node.e)<0){
			node.left=remove(node.left,e);
			return node;//未找到，递归继续，
		}else{
			if(node.left==null){
				Node rightNode=node.right;
				node.right=null;
				size--;
				return rightNode;
			}
			if(node.right==null){
				Node leftNode=node.left;
				node.left=null;
				size--;
				return leftNode;
			}
			//将要删除的结点的左子树的最大值或右子树的最小值替换给要删除的值
			Node successor=minimum(node.right);//找到要删除结点的右子树的最小值
			//把要删除结点的右子树的全部(除开 successor本身)给 successor，左子树的全部给 successor
			successor.right=removeMin(node.right);//把右子树删掉最小值，将产生的新根给 successor.right
			successor.left=node.left;
			node.left=node.right=null;
			size--;
			return successor;
			
		}
		
	}
	//17.打印，重写toString方法，按中序打印
	@Override
	public String toString() {
		StringBuilder sb=new StringBuilder();
		generateBSTString(root,0,sb);//从头结点开始（第0层）,递归的把每一层结点放进去
		return sb.toString();
	}
	private void generateBSTString(BinarySearchTree<E>.Node node, int depth,
			StringBuilder sb) {
		if(node==null){
			sb.append(generateDepthString(depth)+"null\n");
			return;
		}
		//中序遍历
		generateBSTString(node.left,depth+1,sb);
		sb.append(generateDepthString(depth)+node.e+"\n");
		generateBSTString(node.right,depth+1,sb);
	}
	private String generateDepthString(int depth) {//每一层的元素前有多少个空格，根据层数来定
		StringBuilder sb=new StringBuilder();
		for(int i=0;i<depth;i++){
			sb.append("--");
		}
		return sb.toString();
	}
}