无监督学习-主成分分析(Unsupervised Learning-Principle Component Analysis)

#无监督学习-主成分分析
Principle Component Analysis
主成分分析
聚类(Clustering)

HAC层次凝聚的聚类


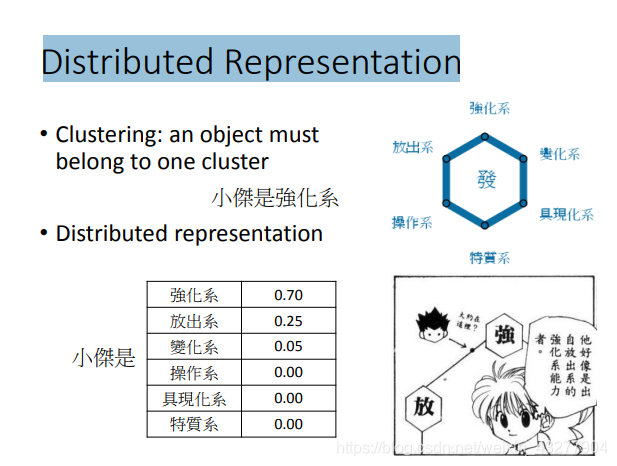
降维
Feature selection
Feature selectio：去掉没用的维度。
PCA

基于特征值分解协方差矩阵实现PCA算法
因为S 是数据的协方差矩阵,所有具有一些性质:

S是对称的(Symmetric)
S是半正定矩阵(Positive-semidefinite): 设S SS为实对称矩阵，若对于每个非零实向量X ，都有XTSX≥0 X^TSX\ge 0X
T
SX≥0，则称A为半正定矩阵，称XTSX X^TSXX
T
SX为半正定二次型。
S SS的特征值(eigenvalues)都是非负的
eigenvector是特征向量
通过推导得到结论:
计算数据矩阵的协方差矩阵，然后得到协方差矩阵的特征值特征向量,选择特征值最大(即方差最大)的k个特征所对应的特征向量组成的矩阵。





基于SVD分解协方差矩阵实现PCA算法
在定义中一个digit由component线性组成,再加一个digit的平均
digit: x xx
digits的平均: x¯ \bar x xˉcomponent线性组成: xˆ \hat x x^x¯ \bar x xˉ和x xx是已知的,目标就是最小化x−x¯ x-\bar xx− xˉ 与xˆ \hat x x^ 之间的重构误差(reconstruction error)



PCA通过神经网络实现
注意这时候W不能保证是正交矩阵