《统计学习方法》—— 统计学习方法概论

前言

最近发现在自然语言处理上，理论知识掌握得还是不够牢靠。因此决定开始钻研李航写的《统计学习方法》，虽然之前系统地自学过机器学习，平时也零散地研究过一些概念和算法，但总归还是担心有些东西只是掌握了皮毛，或者压根就不知道。同时为了达到比较好的学习效果，开始学习画思维导图，同时也把学习笔记整理成文章，作为博客发出来，既为自我督促，也为经营自己的技术博客，塑造好的个人品牌。这也算是部分践行被号称是终极学习法的费曼学习法：One can only learn by teaching. 对目前的我来说，能把学会的东西系统整理出来，表达出来，并能灵活运用，是最终所要追求的。当然，因为时间和精力的限制，下面的内容并不以教学为目的，只能是给有相关知识背景的人士参阅和交流用。

研究完第一章——统计学习方法概论，确实会有更通透的感觉，认知上又提升了不少，收获不小。

思维导图

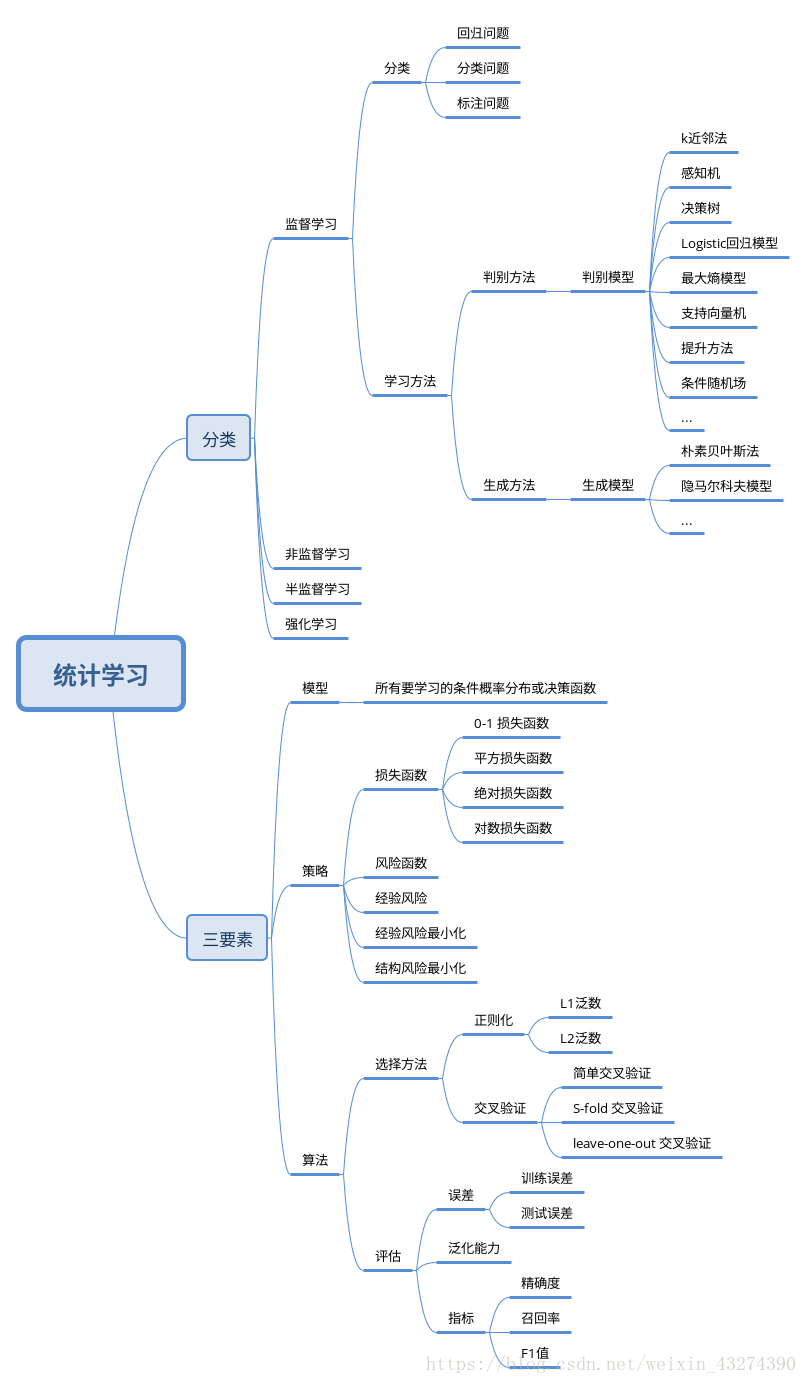
关键概念

统计学习的三要素：模型、策略和算法。

• 模型：所有要学习的条件概率分布或决策函数。
• 策略：模型选择的准则
• 算法：根据学习策略，从假设空间中选择最优模型，并最后考虑用什么计算方法求解最优模型。

研究问题分类

• 回归问题：输入变量和输出变量均为连续变量的预测问题
• 分类问题：输出变量为有限个离散变量的预测问题
• 标注问题：输入变量与输出变量均为变量序列的预测问题。

泛化能力（generalization ability）

• 学习方法对未知数据的预测能力

交叉验证

• 简单交叉验证
• S-fold cross validation：随机地将已给数据切分为S个互不相交的大小相同的子集；然后利用S-1个子集的数据训练模型，利用余下的子集测试模型；将这一过程对可能的S种选择重复进行；最后选出S次评测中平均测试误差最小的模型
• leave-one-out cross validation：S-fold 的特殊情况 S = N，N 为给定数据集的容量。该方法往往在数据缺乏的情况下使用

监督学习模型

• 生成模型：由数据学习联合概率分布P(X,Y)，然后求出条件概率分布P(Y|X)作为预测的模型。
  • P(Y|X) = P(X,Y) / P(X)
• 判别模型：由数据直接学习决策函数f(X)或者条件概率分布P(Y|X)作为预测的模型。

评价指标

• 精确率：P = TP / (TP + FP)
• 召回率：R = TP / (TP + FN)
• F1值：2 / F1 = 1 / P + 1 / R
  
  

认知提升

正则化符合奥卡姆剃刀（Occam’s razor）原理

在所有可能选择的模型中，能够很好地解释已知数据并且十分简单才是最好的模型，也就是应该选择的模型。

正则化是如何实现这一点的？我们把正则化项的前面部分称为第1项，正则化项称为第2项。

如果第1项模型较复杂（有多个非零参数），则第2项的值会较大，这样和要使损失函数尽量小的目标相反。因此，正则化的作用是最终的结果选择经验风险与模型复杂度同时较小的模型。

以前只是简单的记住了一个结论，就是正则化能防止过拟合，这次对正则化的认识又深入了很多。

TODO

#1 为什么叫“似然损失函数”？

对数损失函数（logarithmic loss function），又叫对数似然损失函数（log-likelihood loss function）

#2 如何理解？

贝叶斯估计中的最大后验概率估计（maximum posterior probability, MAP）就是结构风险最小化的一个例子。当模型是条件概率分布、损失函数是对数损失函数、模型复杂度由模型的先验概率表示时，结构风险最小化就等价于最大后验概率估计。

#3 如何理解？

从贝叶斯估计的角度看，正则化对应于模型的先验概率。可以假设复杂的模型有较小的先验概率，简单模型有较大的先验概率。

#4 待深入理解

由Hoeffding不等式，可以推导出泛化误差上界。证明训练误差小的模型，其泛化误差也会小。

该文章在我的个人博客的地址：
http://yuanyu.fr/2018/09/25/statistic-learning-mothods-chapter-1