1.问题
对于下图使用Dijkstra算法求由顶点a到顶点h的最短路径

2.解析
用V1表示已经找到最短路径的顶点,V2表示与V1中某个顶点相邻接且不在V1中的顶点;E1表示加入到最短路径中的边,E2为与V1中的顶点相邻接且距离最短的路径。
步骤 V1 V2 E1 E2
1. {a} {b} {} {ab}
2. {a,b} {d} {ab} {bd}
3. {a,b,d} {c,f} {ab,bd} {dc,df}
4. {a,b,d,c} {f} {ab,bd} {df}
5. {a,b,c,d,f} {e} {ab,bd,dc,df} {fe}
6. {a,b,c,d,e,f} {g} {ab,bd,dc,df,fe} {eg}
7. {a,b,c,d,e,f,g} {h} {ab,bd,dc,df,fe,eg} {gh}
8. {a,b,c,d,e,f,g,h} {} {ab,bd,de,df,fe,eg,gh} {}
求所有顶点对之间的最短路径可以使用Dijkstra算法,使其起始节点从a循环到h,每次求起始节点到其他节点的最短路径,最终可以求得所有顶点对之间的最短路径。
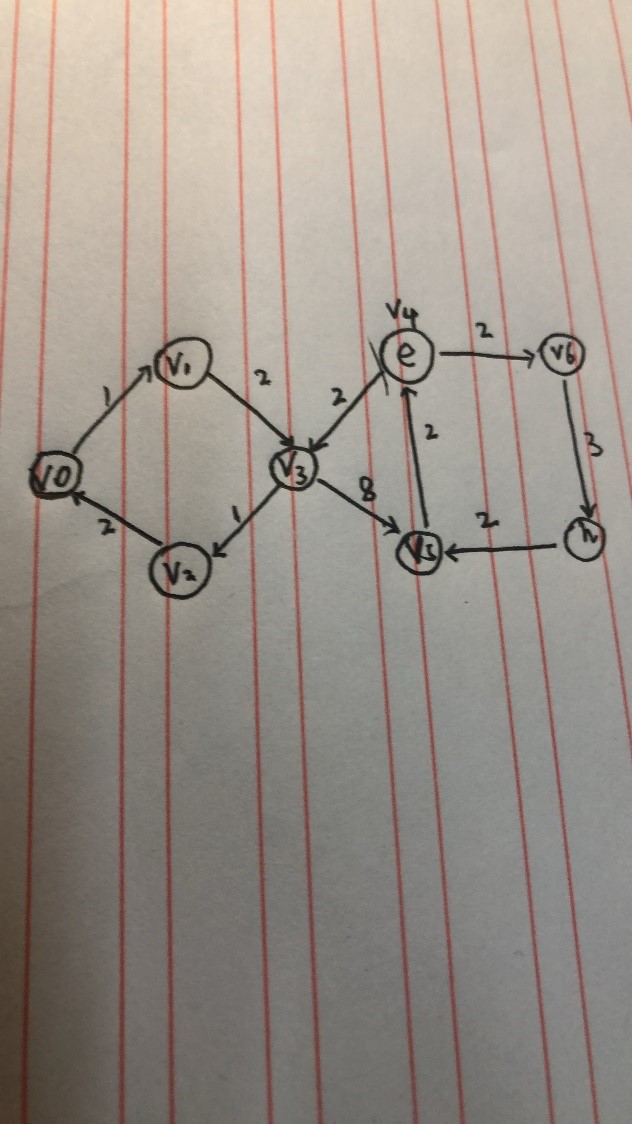
使用二维数组作表存储顶点之间的关系。 将a比作V1,b比作V2依次类推得:
a:V0, b:V1,c:V2, d:V3, e:V4, f:V5, g:V6, h:V7
得到图:
3. 设计
伪代码
算法:Dijkstra(G,s)
//单起点最短路径的Dijkstra算法
//输入;具非负权重加权连通图G = <V , E>以及它的顶点s
//以及路径上的倒数第二个顶点pv
Initialize(Q)
for V中每一个顶点v
dv←;pv←null
Insert(Q, v, dv) //初始化优先队列中顶点的优先级
ds←0; Decrease(Q,s,ds) //将s的优先级更新为ds
VT←Ø
for i←0 to |V|-1 do
u*←DeleteMin(Q) //删除优先级最小的元素
VT←VT∪{u*}
for V-VT中每一个和u*相邻的顶点u do
if du* + w(u*, u) <du
du←du*+w(u*,u); pu←u*
Decrease(Q , u, du)
实验截图:

4. 分析
[算法复杂度推导]
不会推,ԾㅂԾ,,结论:O(n^2)
5. 源码
[github源码地址]
https://github.com/Lin02993/Algorithm-Analysis-and-Practice-on-the-job

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








