LeetCode Python - 54. 螺旋矩阵

---

题目

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

示例 1：

输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]

示例 2：

输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出：[1,2,3,4,8,12,11,10,9,5,6,7]

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 10
• -100 <= matrix[i][j] <= 100

---

答案

方法一

我们用 i 和 j 分别表示当前访问到的元素的行和列，用 k 表示当前的方向，用数组或哈希表 vis 记录每个元素是否被访问过。每次我们访问到一个元素后，将其标记为已访问，然后按照当前的方向前进一步，如果前进一步后发现越界或者已经访问过，则改变方向继续前进，直到遍历完整个矩阵。

时间复杂度 O(m×n)，空间复杂度 O(m×n)。其中 m 和 n 分别是矩阵的行数和列数。

对于访问过的元素，我们也可以将其值加上一个常数 300，这样就不需要额外的 vis 数组或哈希表来记录是否访问过了，从而将空间复杂度降低到 O(1)。

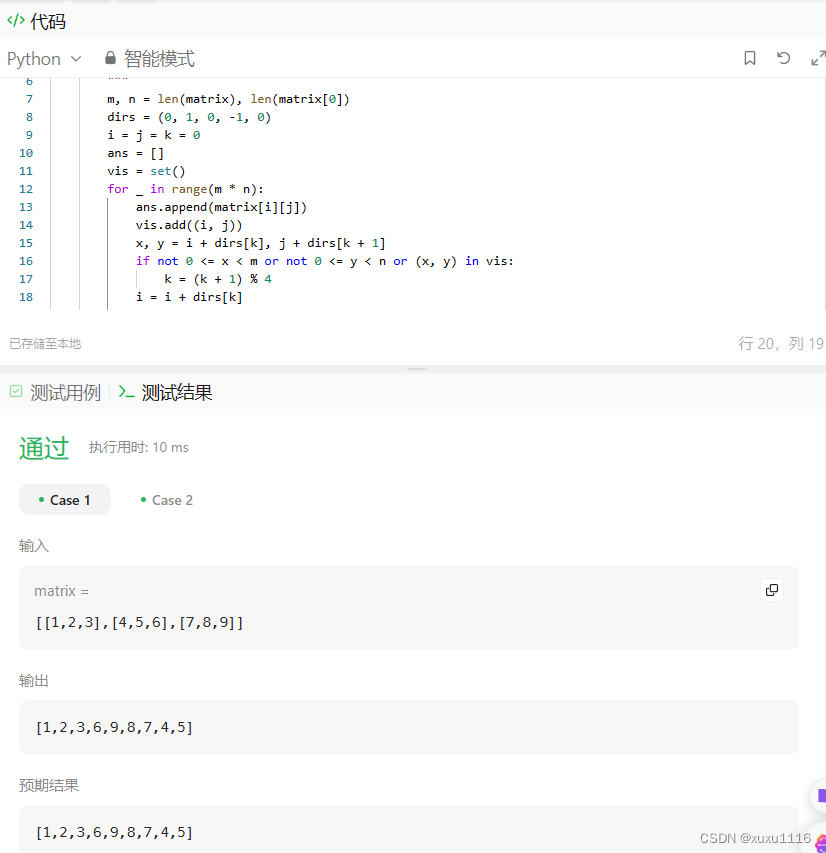
class Solution(object):
    def spiralOrder(self, matrix):
        """
        :type matrix: List[List[int]]
        :rtype: List[int]
        """
        m, n = len(matrix), len(matrix[0])
        dirs = (0, 1, 0, -1, 0)
        i = j = k = 0
        ans = []
        vis = set()
        for _ in range(m * n):
            ans.append(matrix[i][j])
            vis.add((i, j))
            x, y = i + dirs[k], j + dirs[k + 1]
            if not 0 <= x < m or not 0 <= y < n or (x, y) in vis:
                k = (k + 1) % 4
            i = i + dirs[k]
            j = j + dirs[k + 1]
        return ans

方法二：逐层模拟

我们也可以从外往里一圈一圈遍历并存储矩阵元素。

时间复杂度 O(m×n)，空间复杂度 O(1)。其中 m 和 n 分别是矩阵的行数和列数。

class Solution(object):
    def spiralOrder(self, matrix):
        """
        :type matrix: List[List[int]]
        :rtype: List[int]
        """
        m, n = len(matrix), len(matrix[0])
        dirs = (0, 1, 0, -1, 0)
        i = j = k = 0
        ans = []
        for _ in range(m * n):
            ans.append(matrix[i][j])
            matrix[i][j] += 300
            x, y = i + dirs[k], j + dirs[k + 1]
            if not 0 <= x < m or not 0 <= y < n or matrix[x][y] > 100:
                k = (k + 1) % 4
            i = i + dirs[k]
            j = j + dirs[k + 1]
        # for i in range(m):
        #     for j in range(n):
        #         matrix[i][j] -= 300
        return ans

方法三

class Solution(object):
    def spiralOrder(self, matrix):
        """
        :type matrix: List[List[int]]
        :rtype: List[int]
        """
        m, n = len(matrix), len(matrix[0])
        x1, y1, x2, y2 = 0, 0, m - 1, n - 1
        ans = []
        while x1 <= x2 and y1 <= y2:
            for j in range(y1, y2 + 1):
                ans.append(matrix[x1][j])
            for i in range(x1 + 1, x2 + 1):
                ans.append(matrix[i][y2])
            if x1 < x2 and y1 < y2:
                for j in range(y2 - 1, y1 - 1, -1):
                    ans.append(matrix[x2][j])
                for i in range(x2 - 1, x1, -1):
                    ans.append(matrix[i][y1])
            x1, y1 = x1 + 1, y1 + 1
            x2, y2 = x2 - 1, y2 - 1
        return ans

---

运行结果

方法一

方法二

方法三