Leetcode刷题-59. 螺旋矩阵 II_写一个函数,输入变量为整数n,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序-优快云博客

本文链接：https://blog.youkuaiyun.com/ITSOK_123/article/details/123933656

本文详细介绍了LeetCode上的螺旋矩阵II问题的解题思路和解决方案。通过分析题目，提出了从外到内顺时针构造螺旋矩阵的方法，并提供了具体的算法实现。重点讲解了如何控制循环边界和方向变化，以生成满足条件的矩阵。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

解题思路

1.题目描述
2.题目分析
3.题目解答

1.题目描述

给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

示例1：

输入：n = 3
输出：[[1,2,3],[8,9,4],[7,6,5]]

在这里插入图片描述
示例2：

输入：n = 1
输出：[[1]]

2.题目分析

乍一看这题目好像有点无处下手，因为不知道如何进行循环控制。但是我们可以仔细观察题目描述中的矩阵构成其实是一圈圈来构造的，而这个圈数也是与所给的参数n密切相关，于是我们可以想到从一圈圈循环入手。
本题的难点在于编码时间控制循环的边界条件。即使我们已经得出是从圈数来进行入手，由于每圈涉及到繁琐的转向问题，而每次转向的控制又有些难以编码实现。我们可以以示例1中的矩阵进行模拟尝试。

首先第一圈循环的保存顺序依次是1,2,3-转向->4,5-转向->6,7-转向->8
第二圈保存9，最后一圈矩阵保存完毕

我们观察上面第一圈的保存顺序模拟，就可以考虑编码实现了。需要注意的是在编码过程中因为又前后四次循环，所以我们必须保证横向和纵向的循环各自的循环次数是一定的，也就是说我们采用必须1,2,3-->4-->5,6,7-->8-->9;或者1,2-->3,4-->5,6-->7,8这样的循环，也就是说四次循环之间纵向和横向的循环元素是一致的，如果是1,2,3-->4,5-->6,7-->8-->9这类的就是不一致的区间遍历结构，是无法有效编码的。在有效的两种循环中我们发现后者是更加有规律可循的，因此我们考虑每次转向后的循环遍历当前圈的周长/4个元素；
我们按照如下的填充顺序填充矩阵
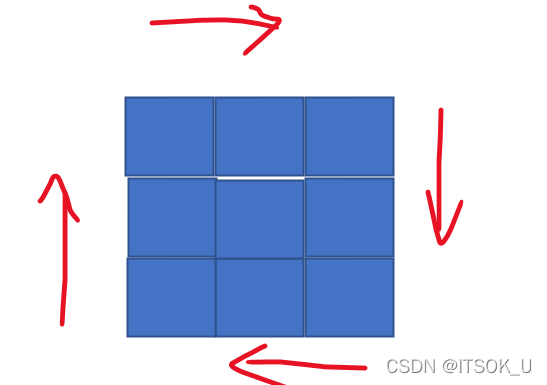
在这里插入图片描述
注意我们按照示例一的输入模拟时最后一圈只有一个元素，而如果输入是偶数的化，就会有着完整的圈数，经过计算我们可以得出对于给定的整数n，构建螺旋矩阵的圈数是n/2，n为奇数的话还要填充最后一个处于最中间的位置的元素。
具体算法可以看下面的代码，已经十分清晰了。

3.题目解答

3.1 从外到内顺时针模拟

class Solution {
   
public:
    vector<vector<int>> generateMatrix(int n) {
   
        vector<vector<int>> res(n,vector<int>(n,0));
        int loop = n/2,mid = n/2;    //循环几圈
        int x =0 ,y=0;      //每圈的起始位置
        int ptr = 1;        //圈内循环计数，用来控制每行每列的元素数
        int val = 1;        //赋值自变量
        //顺时针打印（行列行列）
        while(loop--){
   
            int i =