首先一开始需要提出一个新的问题,那就是在参数更新次数不断增加,loss却趋于一个低值不再减小。一般情况我们会认为这个是遇到local minima了,但是一看梯度的具体值会发现,梯度值并不为0。那么他就有可能是卡在这个两壁之间了,左右横跳,左右都是一样的loss,梯度不为0还在横跳.
并且这种可能性比critical point的可能性大多了,而且一般在掉到最底下之前,就会被其他问题阻挠。


通过上图我们来论证一下卡在两壁之间真比掉到最底下更容易发生吗。
上图是一个很普通的loss值的等高线图,×就是我们要到达的地方。黑点是起始点,如果先把n也就是学习率设为0.01,learning rate会乘以梯度成为移动的距离,所以它其实就是我们迈出的步伐的大小,然后就会发现步伐太大了就跨过了,一直跨过头,就如同×在山谷底,而我们在前后山壁上来回跳。
那如果吧n设的更小一点,让步伐迈小一点呢。首先这个等高线之间其实就是梯度,那么等高线越密集的地方,梯度越密集,也就是梯度越大,所以在一开始还能走很大一步,但是一旦走到这个圈里面了,没有高度的变化了,梯度几乎为0 ,学习率也被设置的很小,那么移动的步伐会非常的小,根本就到不了×这个地方,图里面的这里就是更新100000次仍然只走了这么一点。
那我们发现问题其实就在学习率上面,我们会很轻易的想到,如果在高度变化小的地方,比如下图中沿着这个等高线的方向,或者是线的圈内,这个时候的learning rate大一点就好了,因为这个时候的g小,步伐迈不出去。并且在垂直跨越等高线,g会比较大的时候,learning rate能小一点就好了,这样就不会跨过头,在两壁之间反复横跳了。
所以需要这个learning rate可以自动调整,在坡度大的方向时小,坡度小的方向大。如下图,这里讲的时候假设只关注下标i这个参数,所以所有的都会带有下标i。将n除以一个σ,这个σ与上标t有关。这个σ叫做n这个参数的依赖(parameter dependent)。

先讲第一种简单的σ定义方式,叫做root mean square均方根。公式如下图。
简单来说,这个σ就是把过去所有的g都算均方根,平方相加再开根。它的效果如下右图,假设θ1是一个比较变化平缓的参数,是个平原谷,那么这个上面的蓝色g值都很小,那么σ也会小,σ是分母,所以n就会大。而θ2是一个陡峭谷,它上面有很大的g,那么Σ这个分母就会大,n就会小。这样就达到了让n可以根据在g方向上的变化剧烈与否(g陡峭与否)来相应改变了。


这种方法其实也是有问题的,比如下面这个新月形状的分布图。会发现比如说w1这个横轴方向上,绿色箭头的坡度是陡峭的,而红色箭头也是水平方向,但是它几乎是沿着等高线的,它反而需要大的学习率。所以说在这种比较复杂的error surface上,需要学习率更加动态的调整。
也比如下面的刚才提到的很简单的哪个error surface如果应用均方根的方法试一下,就会发现,在达到中间之后确实会 前进一段,但是很快由于过小的g会调整带来很大的n,导致发生了上下方向的喷发,但是喷发一会之后又会回到水平上的移动,但是不一会儿又会喷发。


那么就有更好的方法来设置σ,就是加权重。这里的α就是加入的权重,它把当前一次的g和有上一个σ带来的过去所有的g值分开,分开给予不同的权值。这个α就是一个超参数,由个人来定义。
下右图其实就是说明了σ这个参数的作用就是平地踩油门,下坡踩刹车。


并且,今天RMSProp和Momentum已经集成叫做Adam,被pytorch内嵌封装了,不需要自己写。
Learning Rate Scheduling
σ还有一个最最最终极升级版,因为在均方根的应用时出现了喷发的情况,所以出现了一种论调,是给n与时间t相关起来,并且是随着t的增加,n逐渐减小,叫做Learning Rate Decay。如下图并且确实解决了喷发问题。
然后除了持续减小,其实还有一种没有被理论验证,没有数学计算支撑的黑科技,那就是warm up,它随时间是先增后减的,有一些文章用到了这个技术,但是都没有给出解释为什么要这么做。
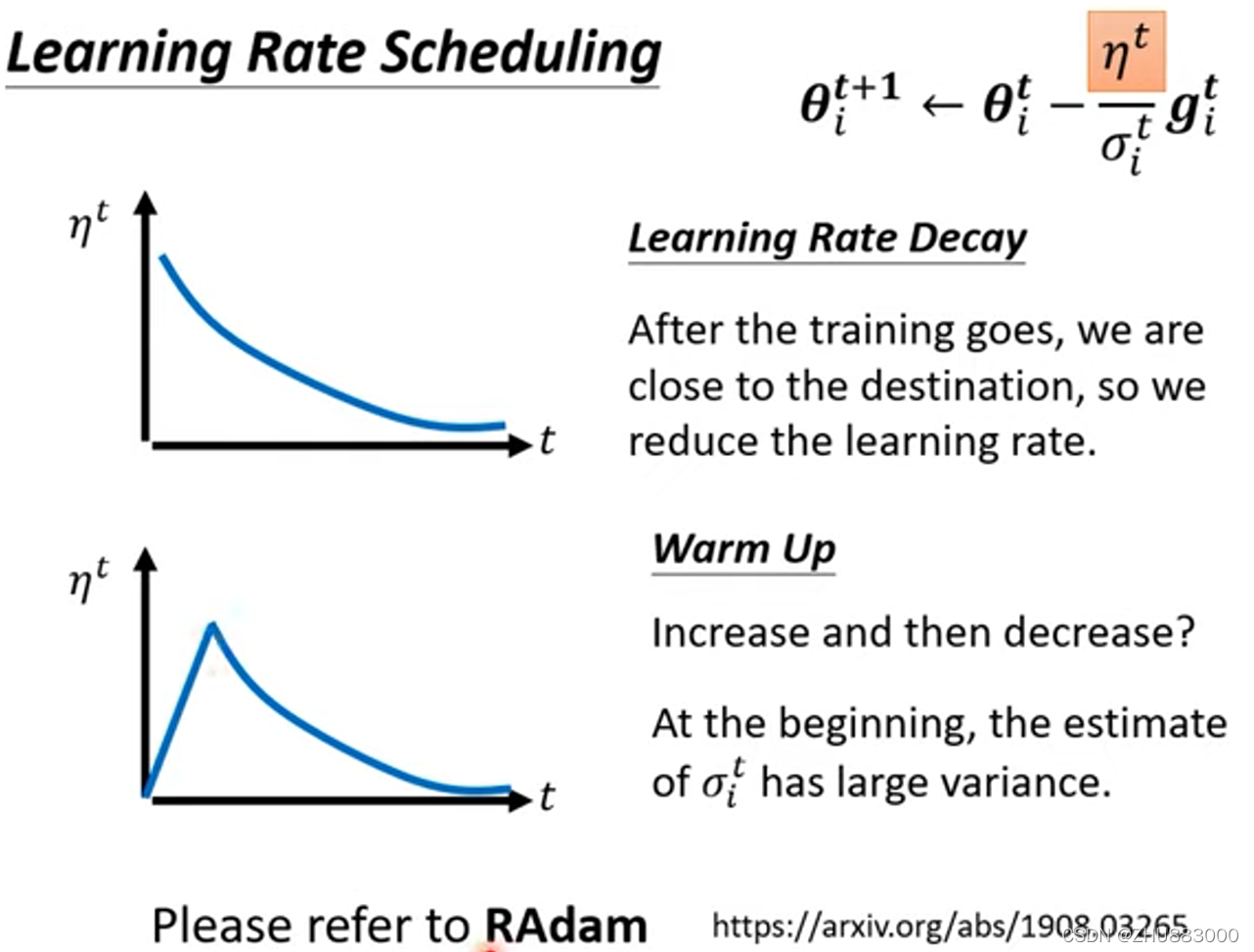

然后这个技术也和momentum一起集成了,叫做RAdam。
上图最后中,虽然三个参数都与t相关,也就是跟每一次的参数更新都有关,但是他们对于g的用法是不一样的,M是考虑方向来计算的,而σ是平方在开放,就只在乎值的大小了。
最后有一些个人的感慨:机器学习确实和数学联系非常紧密,我是指这种思考问题的方式非常相似,你会发现机器学习的发展并不是圈地自乐,他会联系物理联系数学去理解去解释问题,甚至由此解决问题。并且就像从均方根发展到分权重这一步一样,数学中很多问题都有这样的情况和发展路径。
























 6万+
6万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








