1D CNN处理振动数据实现轴承不同故障诊断-python代码

1. 数据描述

数据来自实验室转子齿轮传动实验台，使用三轴振动传感器，共采集了轴承滚动体、外圈、内外混合、正常状态下的四种数据，每种状态，共采集到50000个数据点，因此对应的csv文件包含3列，50000行，三列分别为X,Y,Z三个方向的振动数据。

2. 代码详解

2.1 导入相关库

from keras.models import Sequential
from keras.layers import Dense, Dropout
from keras.layers import Embedding
from keras.layers import Conv1D, GlobalAveragePooling1D, MaxPooling1D
import numpy as np
import keras
import xlrd
import tensorflow as tf
from keras.utils import plot_model
from keras.callbacks import TensorBoard
from keras import regularizers

from time import time
import matplotlib.pyplot as plt
from matplotlib import offsetbox
from sklearn import (manifold, datasets, decomposition, ensemble,
                     discriminant_analysis, random_projection)

2.2 读取数据

写两个读取数据的函数，excel2train以及excel2test，excel2train从原始excel文件中读取前40000个数据点作为训练集，excel2test从原始excel文件中读取后10000个点作为测试集

def excel2train(path):
    data = xlrd.open_workbook(path)
    table = data.sheets()[0]
    nrows = table.nrows  # 行数
    ncols = table.ncols  # 列数
    datamatrix1 = np.zeros((40000,1))
    datamatrix = np.zeros((nrows, ncols))
    for x in range(ncols): #按列存储
        cols = table.col_values(x) #取第x列，返回list型数据
        # np.array创建数组，传递的实参一定是数组，不是tuple。例如，np.array((1,2,3)) # wrong, np.array([1,2,3]), # right
        cols1 = np.array(cols)  # 把list转换为矩阵进行矩阵操作    
        datamatrix[:, x] = cols1 # 把数据进行存储
    # 取前40000个做训练数据，只取第一列，也就是x方向振动数据进行建模
    datamatrix1 = datamatrix[0:40000,0] 
    return datamatrix1

def excel2test(path):
    data = xlrd.open_workbook(path)
    table = data.sheets()[0]
    nrows = table.nrows  # 行数
    ncols = table.ncols  # 列数
    datamatrix1 = np.zeros((10000,1))
    datamatrix = np.zeros((nrows, ncols))
    for x in range(ncols):
        cols = table.col_values(x)
        cols1 = np.array(cols)  # 把list转换为矩阵进行矩阵操作    
        datamatrix[:, x] = cols1 # 把数据进行存储
    datamatrix1 = datamatrix[40000:50000,0] #取第1列，后10000个点建模
    return datamatrix1

读取训练用数据

path1 = 'E:/xxxxxxxxxx' #数据路径
traindata_rollfault = excel2train(path1 + '/滚动体故障/RollFault1000.xlsx')
traindata_innerfault = excel2train(path1 + '/内圈故障/InnerFault1000.xlsx')
traindata_inner_outer_fault = excel2train(path1 + '/内圈+外圈混合故障/InnerOutterFault1000.xlsx')
traindata_normal = excel2train(path1 + '/正常轴承/Normal1000.xlsx')
traindata = np.hstack([rawdata_rollfault, rawdata_innerfault, rawdata_inner_outer_fault, rawdata_normal])

产生训练数据的one-hot标签。这里，样本的shape为(50,10)，即500个数据点划分为一个样本，共得到320个样本，4类故障类型，每类80个样本。

#产生y标签-one-hot编码
x_train = rawdata.reshape(-1,50,10)
print(x_train.shape)
#每类故障的标签个数是80
y_train1 = keras.utils.to_categorical(np.random.randint(1, size=(80, 1)), num_classes=4)
print(y_train1.shape)
y_train2 = keras.utils.to_categorical(np.random.randint(1, size=(80, 1)), num_classes=3)
y_train2 =  np.insert(y_train2, 0, 0, axis=1)
print(y_train2.shape)
y_train3 = keras.utils.to_categorical(np.random.randint(1, size=(80, 1)), num_classes=2)
y_train3 =  np.insert(y_train3, 0, 0, axis=1)
y_train3 =  np.insert(y_train3, 0, 0, axis=1)
print(y_train3.shape)
y_train4 = keras.utils.to_categorical(np.random.randint(1, size=(80, 1)), num_classes=1)
y_train4 =  np.insert(y_train4, 0, 0, axis=1)
y_train4 =  np.insert(y_train4, 0, 0, axis=1)
y_train4 =  np.insert(y_train4, 0, 0, axis=1)
print(y_train4.shape)
y_train = np.vstack((y_train1,y_train2,y_train3,y_train4))
print(y_train)
print(y_train.shape)

读取测试用数据

path2 = 'E:/Datasets/BEIHANG/Bearing/轴承数据20210320/'
testdata_rollfault = excel2test(path2 + '/滚动体故障/RollFault1000.xlsx')
testdata_innerfault = excel2test(path2 + '/内圈故障/InnerFault1000.xlsx')
testdata_inner_outer_fault = excel2test(path2 + '/内圈+外圈混合故障/InnerOutterFault1000.xlsx')
testdata_normal = excel2test(path2 + '/正常轴承/Normal1000.xlsx')
testdata = np.hstack([testdata_rollfault, testdata_innerfault, testdata_inner_outer_fault, testdata_normal])

产生测试数据的one-hot编码。同样的，测试数据每个样本的shape也为(50,10)，即每500个数据点划分为一个样本，共得到80(10000*4/500)个样本

#产生测试数据的table
x_test = testdata.reshape((-1,50,10))
print(x_test.shape)
y_test1 = keras.utils.to_categorical(np.random.randint(1, size=(20, 1)), num_classes=4)
y_test2 = keras.utils.to_categorical(np.random.randint(1, size=(20, 1)), num_classes=3)
y_test2 =  np.insert(y_test2, 0, 0, axis=1)
y_test3 = keras.utils.to_categorical(np.random.randint(1, size=(20, 1)), num_classes=2)
y_test3 =  np.insert(y_test3, 0, 0, axis=1)
y_test3 =  np.insert(y_test3, 0, 0, axis=1)
y_test4 = keras.utils.to_categorical(np.random.randint(1, size=(20, 1)), num_classes=1)
y_test4 =  np.insert(y_test4, 0, 0, axis=1)
y_test4 =  np.insert(y_test4, 0, 0, axis=1)
y_test4 =  np.insert(y_test4, 0, 0, axis=1)
y_test = np.vstack((y_test1,y_test2,y_test3,y_test4))

2.3 创建并训练CNN模型

建立的模型包含7层，分别为一维卷积层、最大池化层、一维卷积层、最大池化层、一维卷积层、最大池化层、全连接层Dense。给每层命名的目的是为了后面用tsne可视化特征时方便查看每层的输出，可视化特征聚类的过程。

model = Sequential()
model.add(Conv1D(filters=64, kernel_size=3, padding='same',activation='relu',name = "Conv1D_1",activity_regularizer=regularizers.l2(10e-4),input_shape=(50, 10)))
model.add(MaxPooling1D(3,name = "MaxP_2"))
model.add(Conv1D(128, 3, padding='same',activation='relu',name = "Conv1D_3"))
model.add(MaxPooling1D(3,name = "MaxP_4"))
model.add(Conv1D(128, 3, padding='same',activation='relu',name = "Conv1D_5",activity_regularizer=regularizers.l2(10e-4)))
model.add(GlobalAveragePooling1D(name = "MaxP_6"))
model.add(Dropout(0.5))
model.add(Dense(4, activation='softmax',name = "Dense_7"))

设置模型训练条件

model.compile(loss='categorical_crossentropy',
              optimizer='adam',
              metrics=['categorical_accuracy'])

模型训练

model.fit(x_train, y_train, batch_size=16, epochs=50,validation_data=(x_test, y_test))

模型测试，手动计算测试精度，该例中，测试精度为97.5%

predict_array = model.predict(x_test)
# 计算测试精度
y_predict = np.zeros_like(predict_array)
y_predict[np.arange(len(predict_array)), predict_array.argmax(axis=1)] = 1 #将每行最大值置1，最大值即为预测标签
temp = np.sum(abs(y_predict - y_test), axis=1) #将y_predict与y_test相减，每一行取绝对值后相加，不为0的元素即为错误预测
temp[temp>0]=1 #将每一行中不为零的数置1
accuracy = (len(temp)-temp.sum())/len(temp)
print("Test accuracy is:", accuracy)

3 tsne特征提取过程可视化

定义函数，用于打印tsne的输出

def plot_embedding(X, title=None):
    x_min, x_max = np.min(X, 0), np.max(X, 0)
    X = (X - x_min) / (x_max - x_min)

    plt.figure(figsize=(6, 6))
    ax = plt.subplot(111)
    for i in range(X.shape[0]):
        plt.text(X[i, 0], X[i, 1], str(y[i]),
                 color=plt.cm.Set1(y[i] / 4.), #colormap 返回颜色
                 fontdict={'weight': 'bold', 'size': 14})

    if hasattr(offsetbox, 'AnnotationBbox'):
        # only print thumbnails with matplotlib > 1.0
        shown_images = np.array([[1., 1.]])  # just something big
        for i in range(X.shape[0]):
            dist = np.sum((X[i] - shown_images) ** 2, 1)
            if np.min(dist) < 4e-3:
                # don't show points that are too close
                continue
    plt.axis([0,1.1,0,1.1])        
    plt.xticks([]), plt.yticks([])#传递空列表来禁用x，y刻度
    ax.spines['top'].set_visible(False)
    ax.spines['right'].set_visible(False)
    ax.spines['bottom'].set_visible(False)
    ax.spines['left'].set_visible(False)
    if title is not None:
        plt.title(title,fontsize=16)

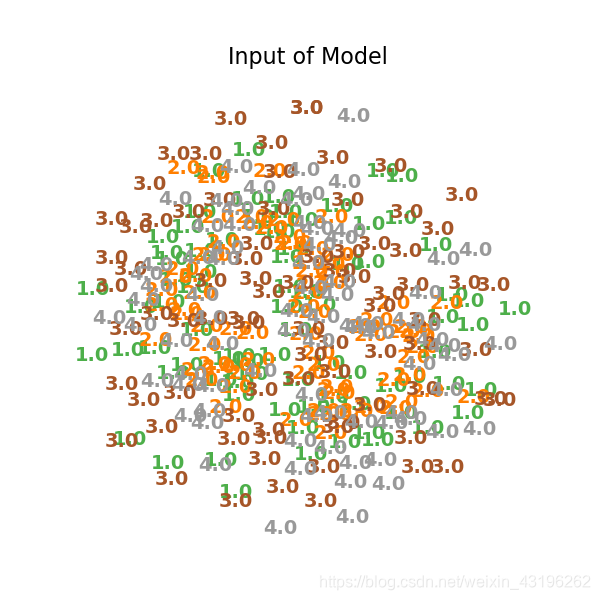
将训练数据原始数据x_train reshape成(320,500)，通过TSNE降维后生成X_tsne，并打印，结果如图所示，可以看到，原始数据通过tsne降成2D后，是非常散乱，同一类型的特征并不聚类。

X = x_train.reshape((-1,500))
# t-SNE数据集
print("Computing t-SNE embedding")
tsne = manifold.TSNE(n_components=2, init='pca', random_state=0)
X_tsne = tsne.fit_transform(X)

plot_embedding(X_tsne,
               "Input of Model")

plt.savefig('E:/xxxxx', dpi = 1000) #图片保存路径
plt.show()

下面打印网络第一层到第七层的输出，代码没有优化，有些啰嗦。
打印第一层，也就是Conv1D层

from keras.models import Model
#取'Conv1D'层 的输出为输出新建为model，采用函数模型
dense1_layer_model = Model(inputs=model.input,outputs=model.get_layer('Conv1D_1').output)
#以这个model的预测值作为输出
dense1_output = dense1_layer_model.predict(x_train)
 
X1 = dense1_output
X1 = X1.reshape((320,-1))
tsne = manifold.TSNE(n_components=2, init='pca', random_state=0)
t0 = time()
X_tsne = tsne.fit_transform(X1)
#print(X_tsne.shape)
plot_embedding(X_tsne,
               "Output of Layer_1")
plt.savefig('E:/xxxxxx', dpi = 1000)
plt.show()

打印第二层

dense2_layer_model = Model(inputs=model.input,
                                     outputs=model.get_layer('MaxP_2').output)
#以这个model的预测值作为输出
dense2_output = dense2_layer_model.predict(x_train)
 
print (dense2_output.shape)
X2 = dense2_output
X2 = X2.reshape((320,-1))
tsne = manifold.TSNE(n_components=2, init='pca', random_state=0)
t0 = time()
X_tsne = tsne.fit_transform(X2)
#print(X_tsne.shape)

plot_embedding(X_tsne,
               "Output of Layer_2")
plt.savefig('E:/xxx', dpi = 1000)
plt.show()

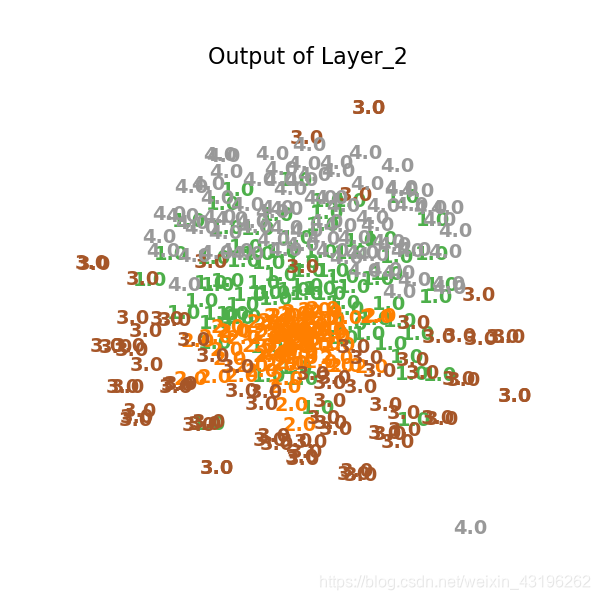
打印第三层，聚类效果初显。

dense3_layer_model = Model(inputs=model.input,
                                     outputs=model.get_layer('Conv1D_3').output)
#以这个model的预测值作为输出
dense3_output = dense3_layer_model.predict(x_train)
 
#print (dense3_output.shape)
X3 = dense3_output
X3 = X3.reshape((320,-1))
tsne = manifold.TSNE(n_components=2, init='pca', random_state=0)
t0 = time()
X_tsne = tsne.fit_transform(X3)
#print(X_tsne.shape)

plot_embedding(X_tsne,
               "Output of Layer_3")
plt.savefig('E:/Datasets/BEIHANG/Bearing/bearing_prediction3.png', dpi = 1000)
plt.show()

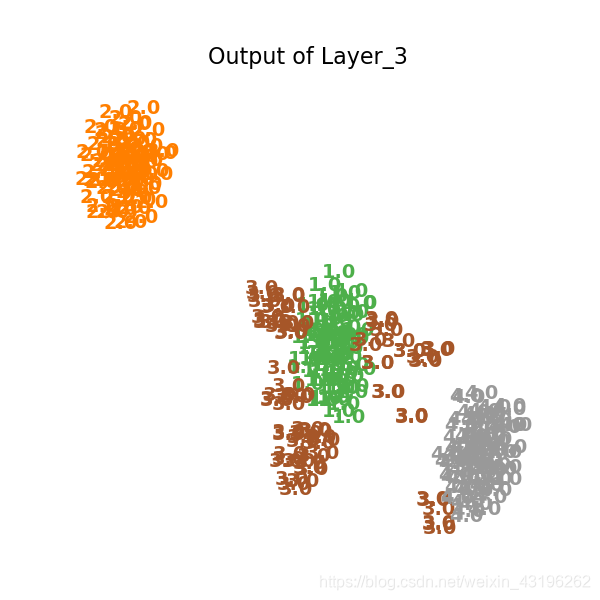
打印第四层，聚类效果更明显

dense4_layer_model = Model(inputs=model.input,
                                     outputs=model.get_layer('MaxP_4').output)
#以这个model的预测值作为输出
dense4_output = dense4_layer_model.predict(x_train)
 
print (dense4_output.shape)
X4 = dense4_output
X4 = X4.reshape((320,-1))
tsne = manifold.TSNE(n_components=2, init='pca', random_state=0)
t0 = time()
X_tsne = tsne.fit_transform(X4)
#print(X_tsne.shape)

plot_embedding(X_tsne,
               "Output of Layer_4")
plt.savefig('E:/Datasets/BEIHANG/Bearing/bearing_prediction4.png', dpi = 1000)
plt.show()

打印第五层，已经能很好聚类了

dense5_layer_model = Model(inputs=model.input,
                                     outputs=model.get_layer('Conv1D_5').output)
#以这个model的预测值作为输出
dense5_output = dense5_layer_model.predict(x_train)
 
print (dense5_output.shape)
X5 = dense5_output
X5 = X5.reshape((320,-1))
tsne = manifold.TSNE(n_components=2, init='pca', random_state=0)
t0 = time()
X_tsne = tsne.fit_transform(X5)
#print(X_tsne.shape)

plot_embedding(X_tsne,
               "Output of Layer_5")
plt.savefig('E:/Datasets/BEIHANG/Bearing/bearing_prediction5.png', dpi = 1000)
plt.show()

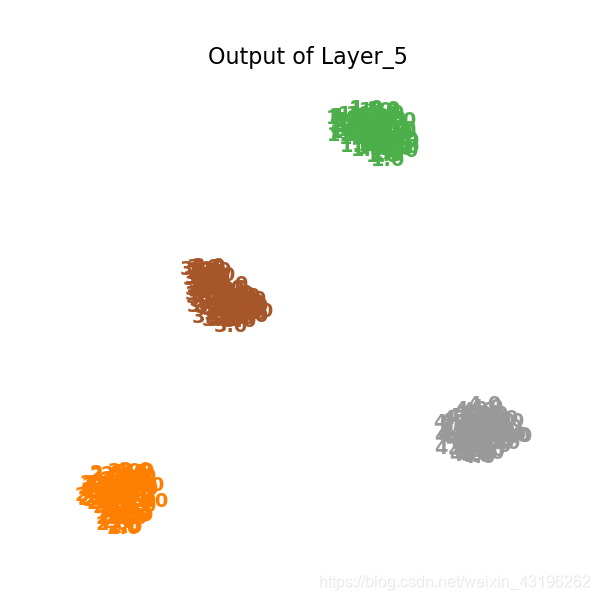
打印第六层

dense6_layer_model = Model(inputs=model.input,
                                     outputs=model.get_layer('MaxP_6').output)
#以这个model的预测值作为输出
dense6_output = dense6_layer_model.predict(x_train)
 
print (dense6_output.shape)
X6 = dense6_output
tsne = manifold.TSNE(n_components=2, init='pca', random_state=0)
t0 = time()
X_tsne = tsne.fit_transform(X6)
#print(X_tsne.shape)

plot_embedding(X_tsne,
               "t-SNE embedding of the bearing_faults(6) ")
plt.savefig('E:/Datasets/BEIHANG/Bearing/bearing_prediction6.png', dpi = 1000)
plt.show()

打印第七层

dense7_layer_model = Model(inputs=model.input,
                                     outputs=model.get_layer('Dense_7').output)
#以这个model的预测值作为输出
dense7_output = dense7_layer_model.predict(x_train)
 
print (dense7_output.shape)
X7 = dense7_output
tsne = manifold.TSNE(n_components=2, init='pca', random_state=0)
t0 = time()
X_tsne = tsne.fit_transform(X7)
#print(X_tsne.shape)

plot_embedding(X_tsne,
               "t-SNE embedding of the bearing_faults(7) ")
plt.savefig('E:/Datasets/BEIHANG/Bearing/bearing_prediction7.png', dpi = 1000)
plt.show()

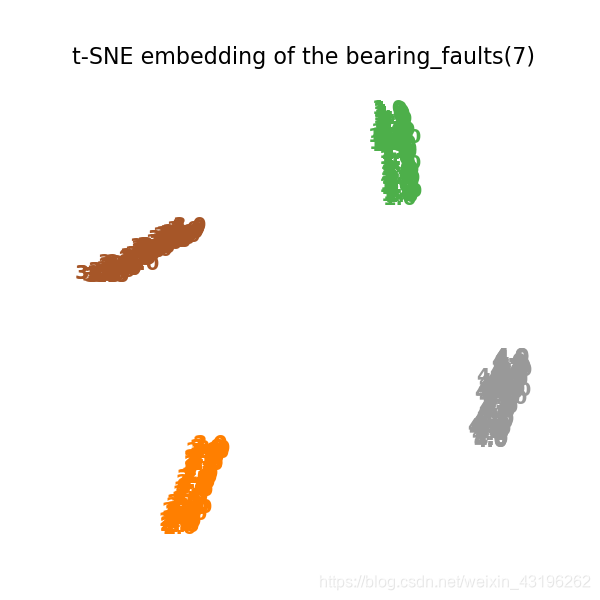
对测试数据的tsne降维可视化是类似的，只需将x_train改成x_test即可，聚类效果与上述类似。
下面展示最终输出的tsne降维图。可以看到，有一个错判的，实际精度97.5%。