LeetCode 399. 除法求值(并查集+BFS)

最新推荐文章于 2023-03-23 16:40:30 发布

只会写臭虫

最新推荐文章于 2023-03-23 16:40:30 发布

阅读量644

点赞数

CC 4.0 BY-SA版权

分类专栏：并查集 LeetCode题解 BFS例题

本文链接：https://blog.youkuaiyun.com/weixin_43175029/article/details/94558925

LeetCode题解同时被 3 个专栏收录

46 篇文章

订阅专栏

BFS例题

9 篇文章

订阅专栏

并查集

4 篇文章

订阅专栏

本文介绍了一种使用图算法解决方程组问题的方法，通过将字符串视为顶点，方程比值作为边权，利用BFS遍历求解从起点到终点的路径边权乘积。代码实现包括并查集、邻接表等数据结构，适用于处理大量查询的场景。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

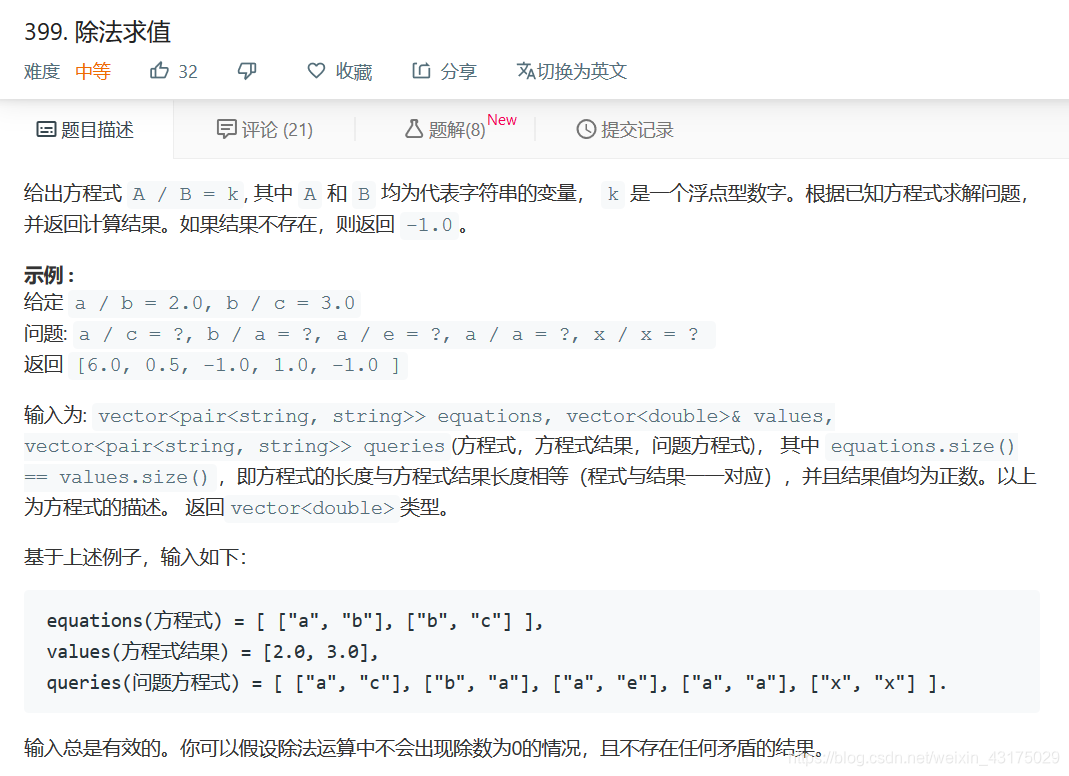
在这里插入图片描述把各个string看做顶点。然后a/b的值看做边。对于每个查询a/b，我们要求的就是从a到b的一条路径，答案就是这条路径上的边权之积。我用的是BFS
代码如下：

class Solution {
public:
    unordered_set<string>st; //存放顶点的集合
    map<pair<string,string>,double>mp; //存放边的权值
    unordered_map<string,string>f;  //并查集数组
    vector<double>ans;
    unordered_map<string,int>vis;  
    queue<string>q;
    unordered_map<string,double>sum; //记录到当前的连乘数值
    unordered_map<string,vector<string>>g;  //领接表
    
    string findx(string &s){
        return s==f[s]?s:f[s]=findx(f[s]);
    }
    void merge(string &s1,string s2){
        string f1=findx(s1);
        string f2=findx(s2);
        if(f1!=f2)
            f[f1]=f2;
    }
    
    double bfs(string start,string end){
        if(start==end)
            return 1.0;
        
        for(auto it:st)  //初始化vis数组
            vis[it]=0;
        while(!q.empty())
            q.pop();
        
        sum[start]=1; //初始化起始点的sum值
        q.push(start);
        
        vis[start]=1;
        while(!q.empty()){
            string front=q.front();
            q.pop();
            for(auto u:g[front]){
                if(vis[u])
                    continue;
                sum[u]=sum[front]*mp[make_pair(front,u)];
                if(u==end)
                    return sum[u];
                q.push(u);
                vis[u]=1;
            }
        }
        return -1;
    }
    
    
    vector<double> calcEquation(vector<vector<string>>& equations, vector<double>& values, vector<vector<string>>& queries) {
        //读入数据
        for(int i=0;i<equations.size();i++){
            vector<string>p=equations[i];
            st.insert(p[0]);
            st.insert(p[1]);
            mp[make_pair(p[0],p[1])]=values[i];
            mp[make_pair(p[1],p[0])]=1/values[i];
            g[p[0]].push_back(p[1]);
            g[p[1]].push_back(p[0]);
        }
        for(auto it:st){  //并查集初始化
            f[it]=it;
            
        }
        for(auto p:equations){
            merge(p[0],p[1]);
        }
                
        for(auto p:queries){
            //判断这两个点是否在集合中
            if(st.find(p[0])==st.end()||st.find(p[1])==st.end()){
                ans.push_back(-1);
                continue;
            }
            if(findx(p[0])!=findx(p[1])){//判断这两个点是否连通
                ans.push_back(-1);
                continue;
            }                  
            double ret=bfs(p[0],p[1]);
            ans.push_back(ret);
        }
        return ans;
              
    }
};