百面机器学习基础部分整理+LeetCode必刷

Week1

特征工程

归一化的方法有哪些？为啥要对数值特征做归一化？

• 归一化的方法主要有（1）Min-Max归一化将结果映射到[0,1],进行等比缩放（2）零均值归一化将数据映射到均值为0标准差为1的分布上
• 通过归一化，梯度下降能够更快的找到最优解。常见的需要归一化的模型有（线性回归、逻辑回归、支持向量机、神经网络等），决策树不需要，以c4.5为例，节点分裂主要依靠特征的信息增益比，与是否归一化无关。

类别型变量编码方式？

• LabelEncoder
• OneHot
• 二进制编码

什么是组合特征，如何处理高维组合特征？

• 为提高模型的拟合能力，在特征工程上往往把一阶离散特征两两组合
• 矩阵分解，比如用户Id和物品Id进行交叉特征，将其分别用k维向量表示

如何有效找组合特征？

• 通过降维的方法，减少两个高维特征组合后需要学习的参数，但是在实际问题中，常常需要多种高维特征，如果简单的两两组合，依然存在参数过多过拟合等问题，并不是所有的特征组合都有意义。
• 可以用类似决策树输出规则的方法寻找组合特征，（利用决策树规则挖掘），FFM DeepFFM

文本特征？

• 有哪些文本表示模型？
  • 词袋模型和n-gram模型，不考虑语序，将文章看成一袋子词，忽略语序。通常将连续出现的N个词形成的词组也放到词袋中去。
  • 主题模型 LDA
  • 词嵌入Embedding

Word2Vec如何工作与LDA有什么区别联系？

• Word2Vec 是一种浅层的神经网络模型，它有两种网络结构，分别是CBOW和Skip-gram。
• CBOW是根据上下文出现的词语预测当前词的生成概率，Skip-gram是根据当前词预测上下文各词的生成概率。
• Word2Vec原理
• LDA是概率图生成式模型，其似然函数可以写成若干条件概率连乘的模式。而Word2Vec为神经网络的形式，似然函数定义在网络输出之上，需要通过学习网络的权重从而得到单词的稠密向量表示。

LeetCode-快排及快排变种快速选择

快排

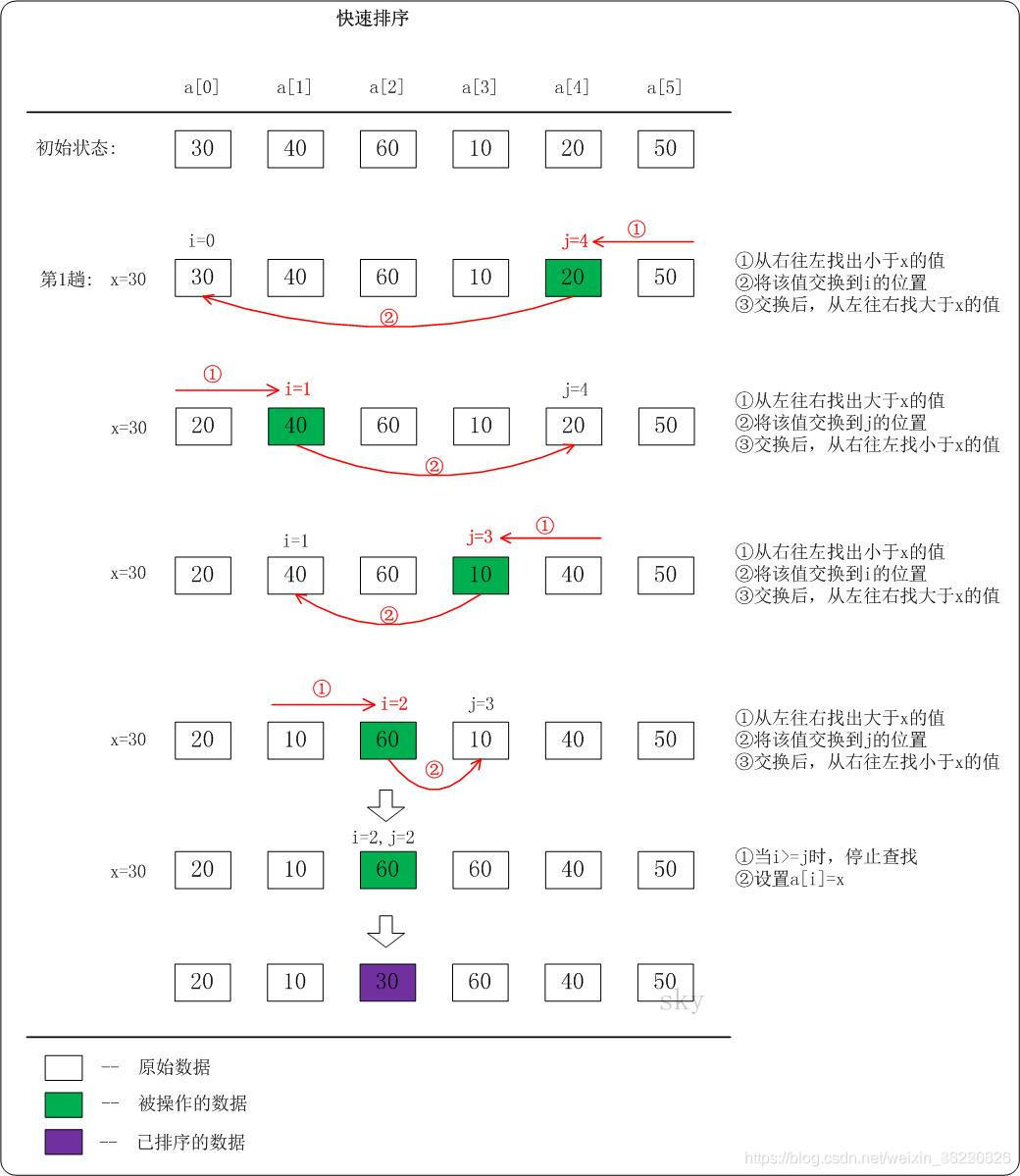
快速排序（英语：Quicksort），又称划分交换排序（partition-exchange sort），通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

• 步骤为：

  从数列中挑出一个元素，称为"基准"（pivot），
  重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区结束之后，该基准就处于数列的中间位置。这个称为分区（partition）操作。
  递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。
  递归的最底部情形，是数列的大小是零或一，也就是永远都已经被排序好了。虽然一直递归下去，但是这个算法总会结束，因为在每次的迭代（iteration）中，它至少会把一个元素摆到它最后的位置去。
  

def quick_sort(alist, start, end):
    """快速排序"""
    if start >= end:  # 递归的退出条件
        return
    mid = alist[start]  # 设定起始的基准元素
    low = start  # low为序列左边在开始位置的由左向右移动的游标
    high = end  # high为序列右边末尾位置的由右向左移动的游标
    while low < high:
        # 如果low与high未重合，high(右边)指向的元素大于等于基准元素，则high向左移动
        while low < high and alist[high] >= mid:
            high -= 1
        alist[low] = alist[high]  # 走到此位置时high指向一个比基准元素小的元素,将high指向的元素放到low的位置上,此时high指向的位置空着,接下来移动low找到符合条件的元素放在此处
        # 如果low与high未重合，low指向的元素比基准元素小，则low向右移动
        while low < high and alist[low] < mid:
            low += 1
        alist[high] = alist[low]  # 此时low指向一个比基准元素大的元素,将low指向的元素放到high空着的位置上,此时low指向的位置空着,之后进行下一次循环,将high找到符合条件的元素填到此处

    # 退出循环后，low与high重合，此时所指位置为基准元素的正确位置,左边的元素都比基准元素小,右边的元素都比基准元素大
    alist[low] = mid  # 将基准元素放到该位置,
    # 对基准元素左边的子序列进行快速排序
    quick_sort(alist, start, low - 1)  # start :0  low -1 原基准元素靠左边一位
    # 对基准元素右边的子序列进行快速排序
    quick_sort(alist, low + 1, end)  # low+1 : 原基准元素靠右一位  end: 最后



if __name__ == '__main__':
    alist = [54, 26, 93, 17, 77, 31, 44, 55, 20]
    quick_sort(alist, 0, len(alist) - 1)
    print(alist)

LeetCode 215 快排变种-快速选择

class Solution(object):
    def findKthLargest(self, nums, k):
        """
        :type nums: List[int]
        :type k: int
        :rtype: int
        """
        def partition(nums, start, end):
            left, right = start+1, end
            pivot = nums[start]
            while left <= right:
                if nums[left] < pivot and nums[right] > pivot:
                    nums[left], nums[right] = nums[right], nums[left]
                    left += 1
                    right -= 1
                elif nums[left] >= pivot:
                    left += 1
                elif nums[right] <= pivot:
                    right -= 1
            nums[start], nums[right] = nums[right], nums[start]
            return right
        def find_k(num, start, end, k):
            split = partition(num, start, end)
            if split == k-1:
                return nums[k-1]
            elif split < k-1:
                return find_k(nums, split+1, end, k)
            elif split > k-1:
                return find_k(nums, start, split-1, k)
        n = len(nums)
        return find_k(nums, 0, n-1, k)
        ######
用快速排序法思想选第K大数，划分函数（左边比pivot处大，右边比其小）用来找到指定范围内pivot处元素（在这个范围）的位置，然后在初始数据选一个数，如果划分函数找到位置=K-1，找到，大于K，小于K再在相应范围里递归地找。

####自己写的 快速选择
class Solution(object):
    def findKthLargest(self, nums, k):
        """
        :type nums: List[int]
        :type k: int
        :rtype: int
        """
        def partition(nums,start,end):
            mid = nums[start]
            low = start
            high = end
            while low<high:
                while low<high and nums[high] >= mid:
                    high -= 1
                nums[low] = nums[high]
                while low<high and nums[low] < mid:
                    low+=1
                nums[high] = nums[low]
            nums[low] = mid
            return low
        def find_k(nums,start,end,k):
            if start==end:
                return nums[start] 
            split = partition(nums,start,end)
            if split == len(nums)-k:
                return nums[len(nums)-k]
            elif split < len(nums)-k:
                return find_k(nums, split+1, end, k)
            else:
                return find_k(nums, start, split-1, k)
        n = len(nums)
        return find_k(nums, 0, n-1, k)
######## 堆排序 留

模型评估

ACC 精确率与召回率

精确率 = TP/TP+FP 召回率 = TP/TP + FN

• 精确率是针对我们预测结果而言的，它表示的是预测为正的样本中有多少是真正的正样本。那么预测为正就有两种可能了，一种就是把正类预测为正类(TP)，另一种就是把负类预测为正类(FP)
• 召回率是针对我们原来的样本而言的，它表示的是样本中的正例有多少被预测正确了。那也有两种可能，一种是把原来的正类预测成正类(TP)，另一种就是把原来的正类预测为负类(FN）
• 当然希望检索结果Precision越高越好，同时Recall也越高越好，但事实上这两者在某些情况下有矛盾的。比如极端情况下，我们只搜索出了一个结果，且是准确的，那么Precision就是100%，但是Recall就很低；而如果我们把所有结果都返回，那么比如Recall是100%，但是Precision就会很低。因此在不同的场合中需要自己判断希望Precision比较高或是Recall比较高。如果是做实验研究，可以绘制Precision-Recall曲线来帮助分析。

ROC曲线-TPR FPR，如何绘制ROC曲线，AUC？

FPR = FP/N TPR= TP/P

• 不断移动分类器的截断点，得到TPR FPR，绘制成ROC
• AUC的物理意义，分类器把正样本排在前面的能力，分类器性能越好

ROC曲线与P-R曲线的特点优劣？

• 当正负样本的分布发生变化时，ROC曲线的形状能够保持不变，P-R曲线的形状一般保持剧烈的变化。ROC曲线能够降低不同测试集带来的干扰，更加客观的衡量模型本身的性能
• 如果更希望看到在特定数据集上的表现，P-R曲线更合适
• 注意TPR用到的TP和FN同属P列，FPR用到的FP和TN同属N列，所以即使P或N的整体数量发生了改变，也不会影响到另一列。也就是说，即使正例与负例的比例发生了很大变化，ROC曲线也不会产生大的变化，而像Precision使用的TP和FP就分属两列，则易受类别分布改变的影响。

为什么对模型路线评估后还要进行A/B测试？

• 离线评估无法完全消除模型过拟合的影响，因此得到的离线评估结果无法完全替代线上评估的结果。
• 离线评估无法还原线上的工程环境
• 线上系统的某些商业指标在离线评估中无法计算，离线评估往往是对本身进行评估。模型上线后（如推荐模型）用户点击率，留存时长PV访问量等变化都要由A/B测试进行全面评估

如何进行A/BTest？

• 进行A/B测试的主要手段是对用户进行分桶，将用户分成实验组和对照组。在分桶的过程中，要注意样本的独立性和采样方式的无偏性，确保同一样本只能分到一个桶中，分桶的userid需要是随机数。
• 对对照组施加旧模型，实验组施加新模型。

超参数调优

• 网格搜索
• 随机搜索
• 贝叶斯优化，似然函数？先验分布，后验分布？

过拟合与欠拟合？

• 增加数据，图像平移、旋转、缩放，生成式对抗网络，和成训练数据。
• 降低模型复杂度，神经网络中减少网络层数、神经元个数，树模型中降低树深度、进行剪枝
• 正则化 L1、L2
• 集成学习 Bagging降低对某一单模型依赖
• ——————————————————
• 增加新特征，组合特征，因子分解机等
• 增加模型复杂度
• 减小正则化系数

LeetCode-滑动窗口

209. 长度最小的子数组

• 可以发现这种算法的魅力所在是left和right一直都在向右移动，所以说复杂度为2*O(N)。其通过不断寻找最长这样一个思想，每次限定了right最小的起始位置，从而舍弃了很多一定不是最优解的计算，达到了O(N)的时间复杂度。

class Solution(object):
    def minSubArrayLen(self, s, nums):
        """
        :type s: int
        :type nums: List[int]
        :rtype: int
        """
        left,minCount= 0,float('inf')
        cumsum = 0

        for right in range(len(nums)):
            cumsum += nums[right]

            while cumsum >= s:
                minCount = min(minCount,right-left+1)
                cumsum = cumsum - nums[left]
                left += 1
        return minCount if minCount != float('inf') else 0

438. 找到字符串中所有字母异位词

class Solution(object):
    import collections
    def findAnagrams(self, s, p):
        """
        :type s: str
        :type p: str
        :rtype: List[int]
        """
        res = []
        need = collections.Counter(p)
        window = collections.Counter()
        valid ,left = 0,0 #valid 用于校验符合的字符的个数
        
        for right in range(0,len(s)) :
            current