洛谷 P1025 数的划分+【POJ - 1664】放苹果(dp)

最新推荐文章于 2024-02-02 19:07:28 发布

只会写臭虫

最新推荐文章于 2024-02-02 19:07:28 发布

阅读量260

点赞数

CC 4.0 BY-SA版权

分类专栏： POJ DP例题

本文链接：https://blog.youkuaiyun.com/weixin_43175029/article/details/94417387

DP例题同时被 2 个专栏收录

10 篇文章

订阅专栏

POJ

3 篇文章

订阅专栏

本文详细解析了如何使用动态规划解决将n个元素分成m组的组合问题，通过两种状态转移方程，即存在空组和所有组均非空的情况，阐述了递归求解的思路，并提供了完整的C++代码实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

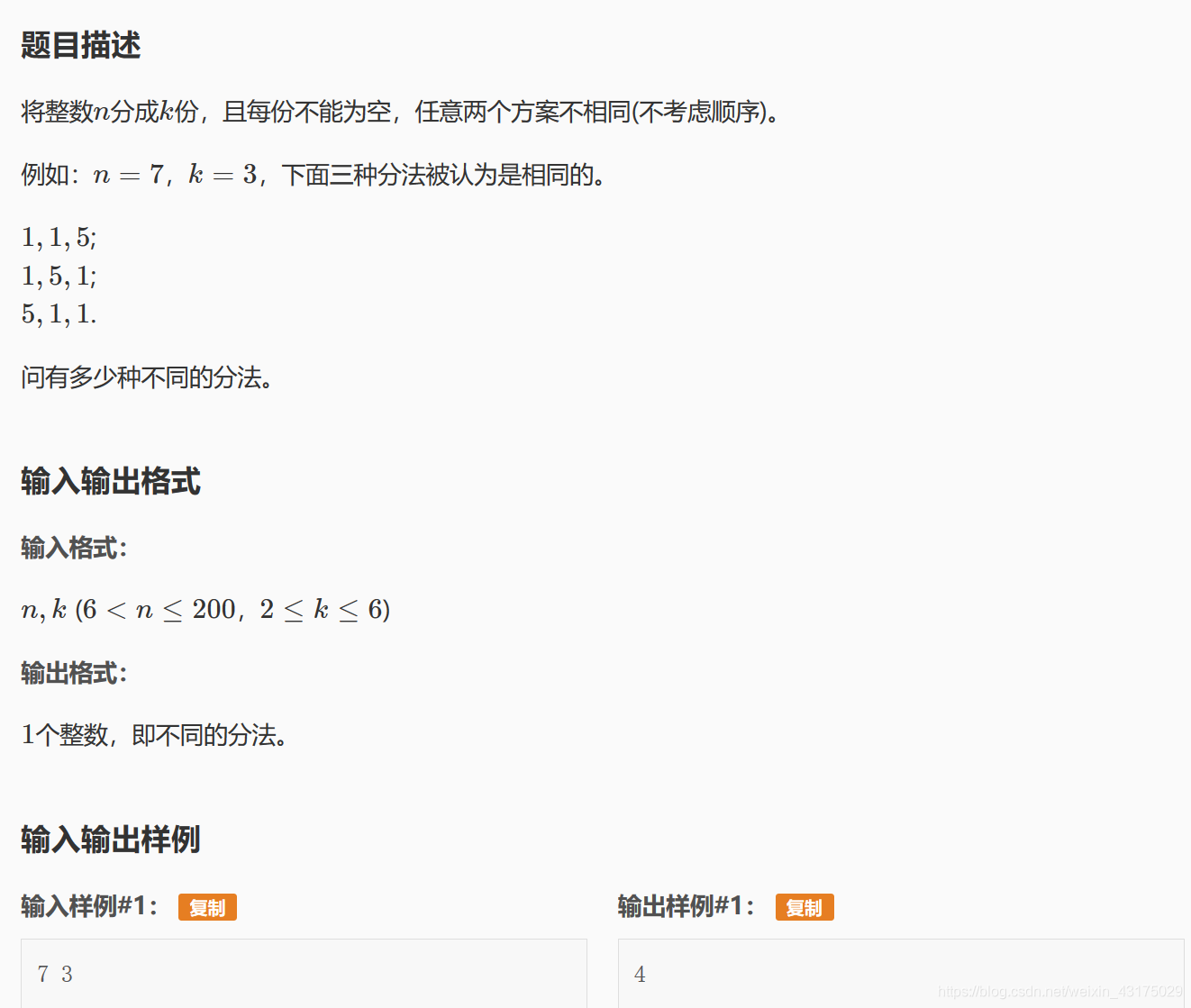
在这里插入图片描述 dp[n][m]表示将n划分为m组的方案数，该状态可能有两种情况：
①至少有一组的数等于1，所以他的上一个状态是: dp[i-1][j-1]
②每一组的数都大于1,所以他的上一个状态是每一组数减1：dp[i-j][j]

#include <stdio.h>
#include <string.h>
#include <cmath>
#include <algorithm>
#include <iostream>
#include<vector>
#include<queue>
using namespace std;

int dp[205][8];

int main()
{
	int n, m;
	cin >> n >> m;
	dp[0][0] = 1;//边界条件
	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= m; j++)
			if (i - j >= 0)
				dp[i][j] = dp[i - 1][j - 1] + dp[i - j][j]; 
			else
				dp[i][j] = dp[i - 1][j - 1];
	cout << dp[n][m];
			
	
	return 0;
}

在这里插入图片描述在这道题中，dp[n][m]表示将n个苹果放入m个盘子的方案数，该状态可能有两种情况：
①该状态至少有一个空盘子，所以他的上一个状态是: dp[i][j-1]
②该状态没有空盘子,所以他的上一个状态是每一组数减1：dp[i-j][j]

边界条件是dp[0][j]=1，表示全是空盘子的情况，可以反推一下边界条件。

#include <stdio.h>
#include <string.h>
#include <cmath>
#include <algorithm>
#include <iostream>
#include<vector>
#include<queue>
using namespace std;

int dp[12][12];

int main()
{
	int t; cin >> t;
	for (int k = 0; k < t; k++) {
		memset(dp, 0, sizeof dp);
		int n, m;
		cin >> n >> m;
		for (int j = 1; j <= m; j++) //边界条件
			dp[0][j] = 1; 

		for (int i = 1; i <= n; i++)
			for (int j = 1; j <= m; j++)
				if (i - j >= 0)
					dp[i][j] = dp[i][j - 1] + dp[i - j][j];
				else
					dp[i][j] = dp[i][j - 1];

		cout << dp[n][m]<<endl;

	}		
	
	return 0;
}