数据结构笔记（一）

最近在做编程题的时候，发现自己的数据结构基础太薄弱，就还是从基础开始学起。

基本概念定义：
数据、数据元素（记录）、数据项（数据不可分割的最小单位）、数据对象（性质相同的数据元素的集合）

物理结构：数据的逻辑结构在计算机中的存储形式。

算法的特性：
输入输出、有穷性、确定性、可行性

一个程序的运行时间，依赖于算法的好坏和问题的输入规模。

算法的时间复杂度：
$T(n)=O(f(n))$，其中f（n）是问题规模n的某个函数。

线性阶、对数阶、平方阶

循环的时间复杂度等于循环的复杂度乘以该循环运行的次数。

算法的空间复杂度：
可以用空间来换取时间。
$S(n)=O(f(n))$，n为问题的规模，f(n)为语句关于n所占存储空间的函数。

线性表：
零个或多个数据元素的有限序列。每个数据元素的类型都是相同的。

线性表的顺序存储结构：

描述顺序存储结构需要的属性：
1）存储空间的起始位置：数组data，它的存储位置就是存储空间的存储位置
2）线性表的最大存储容量：数组长度
3）线性表的当前长度

存储器中的每个存储单位都有自己的编号，这个编号称为地址。

顺序存储结构的插入与删除：
获取位置、插入、删除

线性表顺序存储结构的优缺点：
无须为表示表中元素之间的逻辑关系而增加额外的存储空间；
可以快速地存取表中任一位置的元素；
插入和删除操作需要移动大量元素；
当线性表长度变化较大时，难以确定存储空间的容量；
造成存储空间的”碎片“

线性表的链式存储结构：
用一组任意的存储单元存储线性表的数据元素，这组存储单元可以是连续的，也可是不连续的。
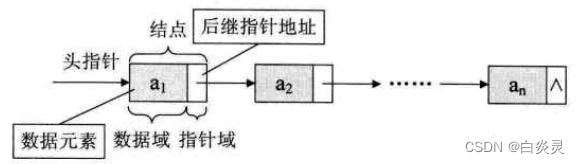
链式结构中，不仅要存数据元素信息（数据域），还要存储它的后继元素的存储地址（指针域）。

数据域和指针域两部分信息组成数据元素的存储映像，称为结点。

单链表的示意图：

单链表的读取：

单链表的插入和删除：

s -> next = p -> next;
p -> next = s 

p的后继结点改成s的后继结点，再把结点s变成p的后继结点。

单链表的删除：

代码：

q = p -> next;
p -> next = q -> next;

对于插入或删除数据越频繁的操作，单链表的效率优势就越是明显。

单链表的整表创建：

单链表的整表删除：

静态链表
用数组描述的链表叫做静态链表。

循环链表：
将单链表中终端结点的指针端由空指针改为指向头结点，就使整个单链表形成一个环，这种头尾相接的单链表称为单循环链表。

双向链表是在单链表的每个结点中，再设置一个指向其前驱节点的指针域。双向链表中的结点都有两个指针域，一个指向直接后继，另一个指向直接前驱。