[剑指Offer学习] ：堆结构理解及堆排序的Java实现

什么是堆结构

堆其实是一种特殊的完全二叉树，完全二叉树的概念，就是自上而下，自左而右，依次的将每一个节点，垒满整棵树，这种树，称之为完全二叉树。当完全二叉树的每一个节点大于等于或者小于等于自己的左右子树时，称该完全二叉树为堆，当堆的顶端是最大的值时，称之为大顶堆，当堆的最顶端为最小值时，称之为小顶端。
我们来看看大顶堆和小顶堆的样子：

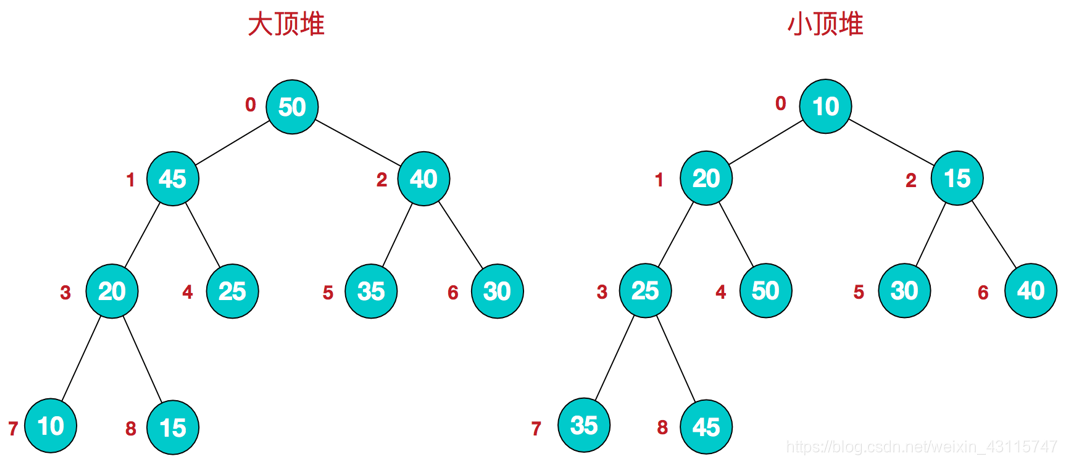
堆排序及其实现逻辑

堆排序虽然引入了堆的概念，但是没有去开销额外的内存去构建一个二叉树，他只是实现了一个“逻辑堆”。
什么是逻辑堆呢？由于完全二叉树是依次垒满的二叉树，所以我们可以将垒好的二叉树从上至下，从左至右的标上序号，如此一来，很容易得出序号为i的节点，其左右子树分别为2i+1，2i+2。而拿大顶堆为例子，其要求便是a[i]>a[2i+1]&&a[i]>a[2i+2]。

堆排序的实现步骤

堆排序的思想如下：
1、构造初始堆，从最后一个非叶节点开始调整
选出叶子节点中比自己大的一个交换，如果交换后的叶子节点不满足堆，则继续调整。

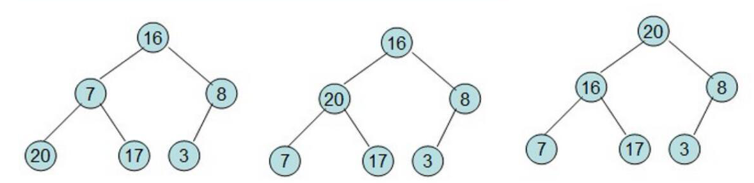
交换后，重新调整：

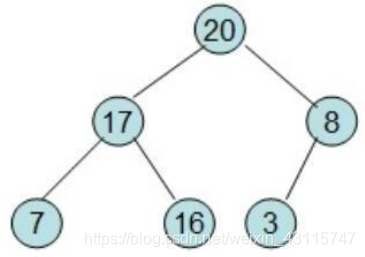
2、构造好初始堆之后，将堆头元素交换到堆尾，堆尾的元素就已经是有序的了，然后一直重复，直到所有都有序。
由此，定义堆排序的过程：
① 由输入的无序数组构造一个最大堆，作为初始的无序区
② 把堆顶元素（最大值）和堆尾元素互换
③ 把堆（无序区）的尺寸缩小1，并调用heapify(A, 0)从新的堆顶元素开始进行堆调整
④ 重复步骤2，直到堆的尺寸为1

堆排序复杂度分析

时间复杂度O(NlogN)：初始化建堆的时间复杂度为O(n)，排序重建堆的时间复杂度为nlog(n)，所以总的时间复杂度为O(n+nlogn)=O(nlogn)。
额外空间复杂度O(1)；
堆排序是不稳定的排序算法，不稳定发生在堆顶元素与A[i]交换的时刻。比如序列：{ 9, 5, 7, 5 }，堆顶元素是9，堆排序下一步将9和第二个5进行交换，得到序列 { 5, 5, 7, 9 }，再进行堆调整得到{ 7, 5, 5, 9 }，重复之前的操作最后得到{ 5, 5, 7, 9 }从而改变了两个5的相对次序。
堆结构非常重要：堆可以搞定几乎所有的贪心算法。

代码展示

public class N5堆排序 {
    public static void main(String[] args) {
        int[] a={1,5,6,8,7,2,3,4,9};
        HeapSort(a);
        for(int i = 0;i<a.length;i++)
            System.out.println(a[i]+ " ");
    }

    //堆排序函数
    public static void HeapSort(int[] a){
        int n = a.length-1;
        //从最后一个非叶子节点开始构造大顶堆
        for(int i = (n-1)/2;i>=0;i--){
            //构造大顶堆，从下往上构造
            //i为树根节点，n为数组最后一个元素的下标
            HeapAdjust(a,i,n);
        }
        for(int i = n;i>0;i--){
            //把最大的数，也就是堆顶放到最后
            //i每次减1，因为药房的位置每次都不是固定的
            swap(a,i);
            //再调整大顶堆
            HeapAdjust(a,0,i-1);
        }
    }

    //构造大顶堆函数，parent为父节点，length为数组最后一个元素的下标
    public static void HeapAdjust(int[] a,int parent,int length){
        //定义临时变量存储父节点中的数据，防止被覆盖
        int temp = a[parent];
        //2*parent+1是其左孩子节点,一路向下遍历左子树
        for(int i = parent*2+1;i<=length;i=i+2+1){
            //如果左孩子大于右孩子，就让i指向右孩子
            if(i<length && a[i]<a[i+1]){
                i++;
            }
            if(temp>=a[i])
                break;

            //如果父节点小于孩子节点，就把孩子节点放到父节点上
            a[parent] = a[i];
            parent = i;  //把交换的孩子节点的下标赋值给parent，让其继续循环以保证大顶堆构造正确
        }
        a[parent] = temp;
    }

    //定义swap函数：用于堆顶元素和最后位置的元素交换
    //注意：这里的最后是相对位置，是在变化的
    public static void swap(int[] a,int i){
        int temp = a[0];
        a[0] = a[i];
        a[i] = temp;
    }
}