矩阵乘法学习

昨天考试，ouyang老师竟然选了数学！还说这是今后noip csp考试的趋势。说实话，我基本就没怎么碰过数学知识，以往学过的也早就忘了。
最终还是不得不面对数学啊……看来得填填《进阶指南》的坑了。

洛咕日爆讲解

某度百科

矩阵乘法，主要是用来求解递推式子时进行加速，其他作用好像就用的比较少了别欺负本蒟蒻，这是老师说的 。按照式子的递推规律构造出一个矩阵以求出之后项的值。在阅读下文前最好了解一下它是怎样进行乘法运算的。
如斐波那契数列：
第一、二项都为一

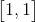
构造出的矩阵

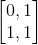
这样

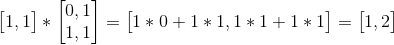
就推出了2,3项。以后的项也可通过多次乘以构造矩阵求得。

而它是怎么加速的呢？实际上是通过快速幂的思想，与数的快速幂类似。因为矩阵乘法具有结合律，所以我们可以直接先求出构造矩阵的次方，最后乘以初始矩阵即可。

例题

Luogu P3390 矩阵快速幂

模板题，需要深刻理解与记忆。

#include<bits/stdc++.h>
using namespace std;

typedef long long ll;
const int mod=1000000007;
ll n,k;

struct mat
{
	ll m[105][105];
}w,o;

mat mul(mat x,mat y)
{
	mat ans;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++) ans.m[i][j]=0;//记得清零
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			for(int k=1;k<=n;k++)
				ans.m[i][j]=ans.m[i][j]%mod+x.m[i][k]*y.m[k][j]%mod;//牢记矩阵乘法规定
	return ans;
}

mat qpow(mat x,ll p)//类似数学快速幂的思想
{
	mat ans=o;
	while(p)
	{
		if(p&1) ans=mul(ans,x);
		x=mul(x,x);//只需把原来的x*x,ans*x改为mul(x,x),mul(ans,x)
		p>>=1;
	}
	return ans;
}

int main()
{
	//freopen("input.txt","r",stdin);
	//freopen("output.txt","w",stdout);
	scanf("%lld%lld",&n,&k);
	for(ll i=1;i<=n;i++)
		for(ll j=1;j<=n;j++) scanf("%lld",&w.m[i][j]);//初始矩阵
	for(ll i=1;i<=n;i++) o.m[i][i]=1;//o矩阵相当于数字1，其他矩阵乘它为该矩阵本身
	mat ans=qpow(w,k);	
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++) printf("%lld ",ans.m[i][j]%mod);
		printf("\n");
	}
	return 0;
}

P1349 广义斐波那契数列

注意构造矩阵，要按照题意，安排p，q的位置。

#include<bits/stdc++.h>
using namespace std;

typedef long long ll;
ll p,q,n,mod;

ll read()
{
	ll x=0,f=1;char ch=getchar();
	while(ch<'0'||ch>'9') {if(ch=='-') f=-1; ch=getchar();}
	while(ch>='0'&&ch<='9') {x=x*10+ch-'0'; ch=getchar();}
	return x*f;
}

struct mat
{
	ll l,r,m[5][5];//l代表矩阵的行数，r代表矩阵的列数，这样两个矩阵相乘时可灵活根据二者的行列数得到答案。
}o,w,b;

mat mul(mat x,mat y)
{
	mat ans;ans.l=x.l,ans.r=x.r;
	for(ll i=0;i<5;i++)
		for(ll j=0;j<5;j++) ans.m[i][j]=0;
	for(ll i=1;i<=x.l;i++)
		for(ll j=1;j<=x.r;j++)
			for(ll k=1;k<=y.r;k++)
				ans.m[i][j]=ans.m[i][j]%mod+x.m[i][k]%mod*y.m[k][j]%mod;//每个数都要取模！！
	return ans;
}

mat qpow(mat x,ll tm)
{
	mat r=o;
	while(tm)
	{
		if(tm&1) r=mul(r,x);
		x=mul(x,x);
		tm>>=1;
	}
	return r;
}

int main()
{
	//freopen("input.txt","r",stdin);
	p=read(),q=read();
	w.m[1][1]=read(),w.m[1][2]=read();w.l=1,w.r=2;
	for(ll i=0;i<5;i++) for(ll j=0;j<5;j++) o.m[i][j]=0;
	o.m[1][1]=o.m[2][2]=1;o.l=o.r=2;
	b.m[1][2]=q,b.m[2][1]=1,b.m[2][2]=p;b.l=b.r=2;//初始化时要将每个矩阵的行数，列数都赋上值。
	n=read(),mod=read();
	if(n<=2) printf("%lld",w.m[1][n]);
	else printf("%lld",mul(w,qpow(b,n-2)).m[1][2]%mod);
	return 0;
}

其他例题

Luogu P1962 斐波那契数列

Luogu P1939 【模板】矩阵加速

Luogu P1306 斐波那契公约数（较难，须推出结论）