4.WebGL+Shader课程基础

WebGL Shader常用外部输入变量

shadertoy变量输入

如果有同学玩过shadertoy一定了解，在这个网站中你可以默认使用一些变量，达到你的目的。经过我最新查阅，目前shadertoy最新外部变量有如下几个：

着色器输入
uniform vec3      iResolution;     // 视口分辨率（以像素为单位）
uniform float iTime; // 着色器播放时间（以秒为单位）
uniform float iTimeDelta; // 渲染时间（以秒为单位）
uniform float iFrameRate; // 着色器帧率
uniform int iFrame; // 着色器播放帧数
uniform float iChannelTime[4]; // 通道播放时间（以秒为单位）
uniform vec3 iChannelResolution[4]; // 通道分辨率（以像素为单位）
uniform vec4 iMouse; // 鼠标像素坐标。xy：当前位置（如果鼠标左键按下），zw：点击位置
uniform samplerXX iChannel0..3; // 输入通道。XX = 2D/Cube
uniform vec4 iDate; // （年、月、日、以秒为单位的时间）

我们在实际中常用的有几个iResolution、iTime与iMouse。因为此网站更加专注于shader的效果，但是我们本教程是基于webgl环境下的shader教程，所以我们需要通过webgl将变量传到shader中。

WebGL Shader变量输入

u_resolution 此变量意思是画布的长和宽

WebGL API中变量赋值

 let resolution = gl.getUniformLocation(gl.program, 'u_resolution');
 gl.uniform2fv(resolution, [512, 512]);

u_time 此变量意思是系统时间

WebGL API中变量赋值

步骤一 获取系统当前时间并赋值

 let utime = gl.getUniformLocation(gl.program, 'u_time');
 let time = (new Date().getTime()) * 0.001;
 gl.uniform1f(utime, time);

步骤二 实时更新时间函数去调取步骤一内容

setTimeout();

u_mouse 此变量意思是系统鼠标位置

步骤一 监听获取鼠标移动事件

canvas.addEventListener('mousemove', mouseMove, true);
//width与height是当前画布的宽和高
function mouseMove(e){
	movex = e.offsetX / width;
	movey = e.offsetY / height;
}

步骤二 赋值给相应的shader变量

let mouse = gl.getUniformLocation(gl.program, 'u_mouse');
gl.uniform2fv(mouse, [movex, movey]);

以上是对于shader输入变量的讨论，至于我们如何应用这些输入的变量创造出效果，后续我们会具体应用，请继续跟我来，baby！

实例

简单讲解下这个例子，这也是我们中级课程中的第一个例子：

1、首先m和p两个变量都是我们上节课给大家讲的将像素坐标进行一个标准化，限定在方便日后操作的区间内：

2、再次t变量是效果的关键，length是一个长度函数，反应的是以鼠标点为中心，根据p点坐标，求得m-p的向量的模。先是这样我们的效果如下面代码所示：（最好配图）图片恰好印证了我们逻辑正确性，越是靠近mose位置说明向量的模越接近与0，越是远离mose，向量的模越是大于1。

precision mediump float;
uniform float u_time;
uniform vec2  u_mouse;
uniform vec2  u_resolution;

void main(void){
    vec2 m =  (u_mouse.xy * 2.0 - u_resolution) / min(u_resolution.x, u_resolution.y);
    vec2 p = (gl_FragCoord.xy * 2.0 - u_resolution) / min(u_resolution.x, u_resolution.y);
    float t = length(m - p);
    gl_FragColor = vec4(vec3(t), 1.0);
}

3、继续我们的理解，此时我们如果扣上sin值，众所周知，sin值最大特点就是返回的值循环变化，（后面我们讲解函数专栏，会给大家详细讲解）。随着m-p向量的模越大，我们sin值是在[-1,1]，之间不断震荡，此时p点再某个位置，sin返回的值又恰好等于0，所有有存在黑色带。请结合下面sin函数的图片仔细思考：

4、*30.的目的自然是让我们sin函数的值震荡区间更加频繁，也就是我们数学上长说的周期更短。

5、至于在加上time*5.的目的是让我们sin函数成波纹状态，动态变化。

precision mediump float;
uniform float u_time;
uniform vec2  u_mouse;
uniform vec2  u_resolution;

void main(void){
    vec2 m =  (u_mouse.xy * 2.0 - u_resolution) / min(u_resolution.x, u_resolution.y);
    vec2 p = (gl_FragCoord.xy * 2.0 - u_resolution) / min(u_resolution.x, u_resolution.y);
    float t = sin(length(m - p) * 30.0 + u_time * 5.0);
    gl_FragColor = vec4(vec3(t), 1.0);
}

坐标系统

回忆WebGL 中的坐标系统

经历了WebGL中坐标变换，最终来到屏幕坐标系，在屏幕坐标系渲染片元像素值的时候就是我们本节课shader的使命。

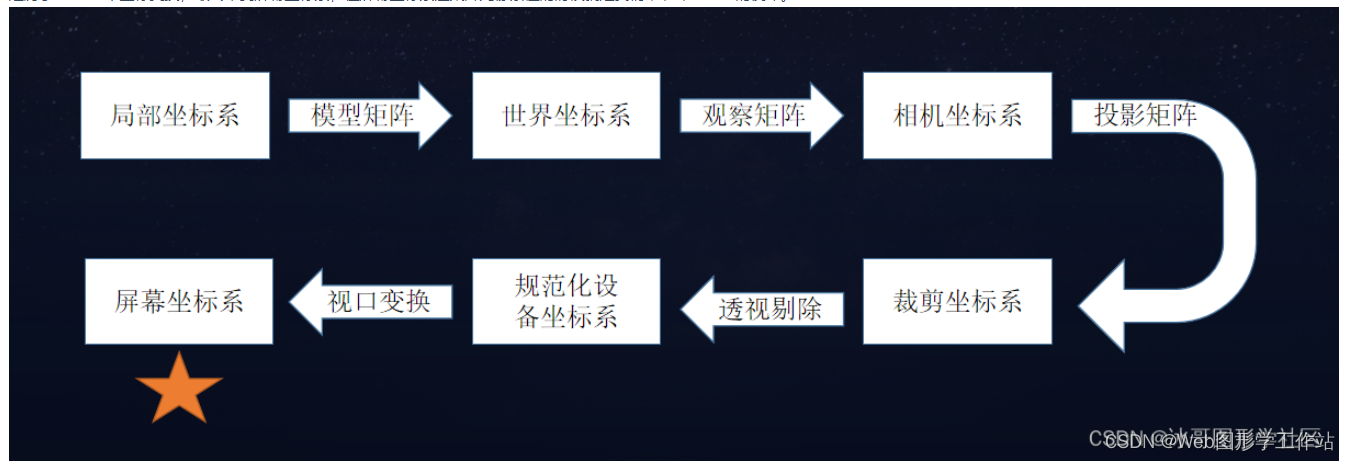
下图是我将shader中的关键性坐标系做了类比：

WebGL Shader中坐标系统

gl_FragCoord

gl_FragCoord是片元着色器坐标系，他的原点在左下角，y轴正方向向上延伸，x轴正方向向右延伸。
为了验证此条结论，我们将gl_FragCoord在代码中做了相应的体现。
如右图所示：
左下角颜色值是vec2（0.，0.，0.，1.），第一个和第二参数都是0，所以呈现是黑色满足在原点的规律。
右上角颜色值是vec2(1.,1.,0.,1.)，第一个和第二参数都是1，所以呈现是黄色满足规律。
下图是片元着色器中执行代码：

#ifdef GL_ES
precision mediump float;
#endif
uniform vec2  resolution;
void main() {
    vec2 p = gl_FragCoord.xy/resolution;
    gl_FragColor = vec4(p.xy, 0.0, 1.0);
}

接下来我们的目标是将我们gl_FragCoord坐标原点移动到画布的中心，这里我们采用的方法是gl_FragCoord.xy坐标各自减去.5。很多同学对这里存在疑惑：为什么是减去，又为什么是0.5？

（1)首先为什么是0.5.

vec2 p = gl_FragCoord.xy/resolution;

我们先将坐标系范围明确到[0,1]之间，因为gl_FragCoord默认坐标区间是[resolution.x,resolution.y]；
我们常用的是坐标原点在画布中间去进行后续的编程。减去0.5，数值目的是让其范围在[.5,.5]。
(2)为什么是减去呢？
我们以左下角的点为例子，当原点在做下角的时候其点位在坐标是（0,0），如果我们将坐标系移动到原点，那此时改点坐标值会变成（-.5，-.5）。从（0,0）=>(-.5,-.5)中间经历的变换就是横纵坐标分别减去.5.所以是减法。
以此类推，因为范围中所有点都是满足此线性变换，所以都是应该是减去-.5.
*注： vec2 p = gl_FragCoord.xy/resolution;此处存在缺陷，因为在实际情况中画布的宽高比是不等于1的， 如果按照此比例去绘制图形会出现拉伸情况，我们后面再一起讨论如何对此进行优化。

具体的变换过程如下所示，我将逐行，逐字符去解释，

vec2 uv = gl_FragCoord.xy*2./resolution.xy;  
uv-=1.; 
uv.x*=resolution.x/resolution.y; 

步骤一

首先画布区间分别除画布长宽，即可将uv定义在[0.,2.]区间内。

步骤二

将坐标系xy分别减去1.，即可将坐标原点移动到画布的正中心。

步骤三

此处存在缺陷，因为在实际情况中画布的宽高比是不等于1的，如果按照此比例去绘制图形会出现比例拉伸情况。为解决此问题，我们进行以下操作：

uv.x*=resolution.x/resolution.y; 

相对比例大的长度除以比例小的长度，得到的是比值乘以当前比例长的数值所对应的坐标uv.x，其目的是将uv.x变化率与uv.y变化率进行同步。结果如下代码所示：

vec2 uv = gl_FragCoord.xy*2./resolution.xy;  
uv-=1.;
uv.x*=resolution.x/resolution.y; 

如果上述从数学角度去分析，uv.x乘上一个正整数倍数，那么每个单元标量所代表的长度就会拉长，这样就会和y轴单元标量变化比率保持一致。

**注:**这里的 uv-=1.;uv.x*=resolution.x/resolution.y;是不能颠倒位置的。绿色和橙色的线是本应该移动距离（-1.，1.），但是如果我们假设先让我们uv.x乘上某个值，比如点（0.3,0）那么此时点的坐标发生变化，若此时再去移动（-1,1.），原点（绿色点）的位置就不在中间位置。

步骤四

以上基本已经达到我们的目标，但是犹豫其代码复杂度较高，我们进行以下简写：

vec2 p = (gl_FragCoord.xy*2. - resolution.xy) / min(resolution.x, resolution.y);

这里面应用 min(resolution.x, resolution.y)的目的是将uv.x与uv.y的变化率进行了同步，并且按照最小的比例长度进行计算。如下图所示：橙色的长方形是当前画布的颜色，绿色是修正后的着色器绘制区。

**注：**实际上我们uv坐标进行了坐标系转换，我们在之后内容中提到mouse鼠标点也可以应用此方法，将值的变化范围定格你想的区间。但是mouse坐标系和gl_FragCoord坐标系的原点位置和y轴方向大家一定要注意区分哈。

let mouse = (u_mouse.xy * 2.0 - u_resolution) / min(u_resolution.x, u_resolution.y);

这是不是非常cool，实际上这为我们后续的操作带来极大方便（还记得我们在初级课程中给大家讲到rgb颜色范围是在[0,1]区间内哦，我们这样做其实也方便了我们将uv位置关系和颜色做一个挂钩，也方便我们去检索逻辑上的bug，以后你或许会更加明白！*

gl_PointCoord

gl_PointCoord坐标原点是在点的左上角，同样我们为了验证结论，我们采用如下代码进行测试：

#ifdef GL_ES
precision mediump float;
#endif
uniform vec2  resolution;
void main() {
    gl_FragColor = vec4(gl_PointCoord.xy, 0.0, 1.0);
}

通过下图我们可以得到左上角的颜色值是vec2（0,.，0.），右下角颜色值vec2（1.，1.），这样可以验证左上角坐标即为我们的0，0点咯。

二者关系

二者之间的关系是相对的，同一个像素点在不同的坐标系范围内，被表示的值也是不一样的，因为二者参考坐标系是不一样的。

WebGL shader颜色计算

自然界中的颜色

自然界中主要有3种颜色分别是R(红)G(绿)B(蓝)这3种是最基本的颜色,称为三基色。它的颜色混合方式就好像有红、绿蓝三盏灯,当它们的光相互叠合的时候色彩相混,而亮度却等于两者亮度之总和,越混合亮度越高。红、绿、蓝三个颜色通道每种色各分为255阶亮度在0时“灯”最弱时候是关掉的,而在255时“灯”最亮。当三色数值相同时为无色彩的灰度色而三色都为255时为最亮的白色都为0时为黑色。同时颜色会相加，并向中间靠拢，最终形成新的色系。

这里介绍一个中国色的网站，网站做的非常出色，有兴趣的朋友学习。http://zhongguose.com/#danfei

Shader中的颜色

shader中颜色是对自然界中颜色的仿真与模拟，具有和自然界中颜色类似的效果。以下将shader中颜色特性做解释：
1.颜色分为红®，绿(g)，蓝(b)，透明度(a)是个值，组合为个4维向量(r,g,b,a)。
2.每个分量的范围是0->1的浮点数，即颜色值/255
3.可以每个分量进行加减乘除计算，也可对整个颜色向量进行加减乘除计算。
常用颜色距离:

(0.0,0.0,0.0,0.0): 黑色 
(1.0,1.0,1.0,1.0): 白色
(1.0,0.0,0.0,1.0): 红色
(0.0,1.0,0.0,1.0): 绿色
(0.0,0.0,1.0,1.0): 蓝色

Shader颜色计算

左边颜色可以表示为：

color1
vec3(1.) 
vec3(0.)

右边颜色可以表示为：

color2
vec3(1.,1.0.)
vec3(0.)

问题：想从左边颜色转换为右边颜色如何计算呢？
答：
左边颜色乘上vec3(1.,1.0.)即可转为右边颜色。
因为在shader里面 黑色乘上任何数字都是黑色，白色乘上任何数字都是乘上的这个数所表示的颜色。

Shader颜色计算常见问题

经常遇到问题：
1、底色比如是黑色，无论乘上什么数都还是黑色；
2、如果是白色，乘以什么就是他本身。
3、底色是黑色，加上什么颜色就是颜色本身。
4、如果颜色系数小于0，那么返回的效果也都是黑色。
5、如果颜色系数大于1，那么返回的效果也都是白色。
注：shader的核心在于数学公式，在于数字的加减乘除，我们的学习过程一定是不断的学习数学，并且总结数学，将规律封装成关键公式去使用。

WebGL Shader颜色输出与打印

为什么要打印颜色？

想一想我们在应用这些语言在打印的时候目的是为了什么呢？答案是调试。以下将不同语言中的打印进行了枚举，供大家欣赏：

Java：System.out.println();
C#：Debug.WriteLine();
JS：console.log();

但是Shader里面目前没有console.log(),没有alert()，更没有什么debugger，也没有F12开发者模式，因为shader的特殊性（GPU渲染完数据在显存，回传内存的唯一方式glReadPixels函数），我们之前调试工具都是在CPU里面进行，目前GPU的调试工具实现比较难，我相信未来一定可以实现变量数值的调试！也许那时候三维编程更加简单！
所以只能通过观察颜色变化，来获取某一节点的数值，通过数值来观察程序的异常，说实话这种情况在实际应用不是很多，大多数通过函数图形或者逻辑推演（我们在中级课程中给大家讲解）的方式进行。但是颜色打印对于毫无头绪的bug，真的是很实用的工具！

如何打印颜色值？

我们以webgl1为例子：
像素读取的时候是按照一个个小长方形进行读取，明确长方形左下角x，y坐标系，在确定起长和高，即可明确长方形的大小，进而将整个读取的数据放到提前声明好的类型化数组里面。
x：指定从矩形像素块的左下角。
y：指定从矩形像素块的左下角。
width：指定矩形宽度。
height：指定矩形高度。
format：指定像素数据格式。gl.ALPHA 、gl.RGB、gl.RGBA。
type：

gl.UNSIGNED_BYTE
gl.UNSIGNED_SHORT_5_6_5
gl.UNSIGNED_SHORT_4_4_4_4
gl.UNSIGNED_SHORT_5_5_5_1
gl.FLOAT

pixels：
要将数据读入的对象。数组类型必须匹配参数的类型

Uint8Array  =>  .gl.UNSIGNED_BYTE
Uint16Array  =>  .gl.UNSIGNED_SHORT_5_6_5gl.UNSIGNED_SHORT_4_4_4_4gl.UNSIGNED_SHORT_5_5_5_1
Float32Array  => .gl.FLOAT

常见异常

如果不是可接受的值，则会引发错误。gl.INVALID_ENUMformattype
如果出现以下情况，则会引发错误。gl.INVALID_OPERATION
type是和不是。gl.UNSIGNED_SHORT_5_6_5formatgl.RGB
type是和不是。gl.UNSIGNED_SHORT_4_4_4_4formatgl.RGBA
type与 的类型化数组类型不匹配。pixels
如果当前 绑定帧缓冲未完成。gl.INVALID_FRAMEBUFFER_OPERATION

WebGL Shader 变量、矢量、矩阵、结构体、数组、函数、限定词、预处理

变量

变量定义

GLSL ES 语言的变量，需要遵循以下原则：

1. 变量名只能包含英文字符、数字和下划线即(a-z、A-Z、0-9、_)
2. 变量名的首字母不能是数字
3. 不能以 gl_ 、webgl_ 或 webgl 开头，这些前缀已经被OpenGL ES 保留了
4. 不能是GLSL ES内置的关键字和保留的关键字

GLSL ES 关键字

attribute	bool	break	bvec2	bvec3	bvec4
const	continue	discard	do	else	false
float	for	highp	if	in	inout
int	invariant	ivec2	ivec3	ivec4	lowp
mat2	mat3	mat4	medium	out	precision
return	sampler2D	samplerCube	struct	true	uniform
varying	vec2	vec3	vec4	void	while

GLSL ES 保留字

asm	cast	class	default
double	dvec2	dvec3	dvec4
enum	extern	external	fixed
flat	fvec2	fvec3	fvec4
goto	half	hvec2	hvec3
hvec4	inline	input	interface
long	namespace	noinline	output
packed	public	sampler1D	sampler1DShadow
sampler2DRect	sampler2DRectShadow	sampler2DShadow	sampler3D
sampler3DRect	short	sizeof	static
superp	switch	template	this
typedef	union	unsigned	using
volatile

变量基本类型

基本类型

GLSL ES中变量类型中的基本类型主要有布尔类型、整形和浮点型。

变量类型	说明
bool	布尔类型，该类型的变量表示一个布尔值即 true或false
int	整型，该类的变量表示一个整数
float	单精度浮点数类型，该类型的变量表示一个单精度的浮点数

类型转换

使用等号（=）可以将值赋给变量，GLSL ES 是强类型语言，如果等号左右两边的变量类型不一样，会报错的哈。例如：在语义上 1 和 1.0 是一个值，但是将 1 赋值给浮点型变量时会出错。

转换	函数	描述
转换为整型数	int(float)	去掉浮点数小数部分，转换为整型数
	int(bool)	true 转换为1，false 转换为0
转换为浮点点	float(int)	将整型数转换为浮点数
	float(bool)	true 转换为1.0，false转换为0.0
转换为布尔值	bool(int)	0转换为false，非0转换为true
	bool(float)	0.0 转换为false，非0转换为 true

矢量

矢量类型

向量指的是具有大小（Magnitude）和方向（Direction）量。在物理学中也称为矢量。向量的表示通常使用小写字母上面加上向右的箭头→表示，或者使用粗体的小写字母表示。向量具有平移不变形。向量只与大小和方向有关系，和向量的起点和终点没有关系。向量也只包含两个属性：大小和方向。

对于空间中的两个点𝐴和𝐵，从𝐴到𝐵的向量可以表示为𝐴𝐵，计算方法为𝐴𝐵=𝐵−𝐴。这块大家要留意一下，就是向量的表示方法和实际的顺义是相反的哈（我记得高中时候数学老师经常强调这一点，不然有的时候求出来的角度是不对的）。

GLSL ES支持矢量类型，这种数据类型适合用来处理计算机图形。矢量类型的变量包含多个元素，每个元素是一个数值（整型数、浮点数或布尔值)。矢量将这些元素排成一列，可以用来表示顶点坐标或颜色值等。

矢量类型介绍

变量类型	说明
vec2, vec3, vec4	具有2、3、4个浮点数元素的矢量
ivec2, ivec3, ivec4	具有2、3、4个整形元素的矢量
bvec2, bvec3, bvec4	具有2、3、4个布尔值元素的矢量

向量代数表示

$$\overrightarrow{oa}=\left[\begin{array}{c}4\\ 3\end{array}\right]$$
如果此时求向量oa的转置：
$$\overrightarrow{oa}=\left[\begin{array}{cc}4& 3\end{array}\right]$$

矢量构造、赋值与取值

构造

在GLSL ES中，矢量非常重要，所以GLSL ES提供了丰富灵活的方式来创建矢量。请重点体验下下面的构造方法

vec3 v3 = vec3(1.0,1.2,1.5); //传入三个分量
vec2 v2 = vec2(v3);  //传入单个分量，其他自动填充
vec4 v4 = vec4(1.0);  vev4 v4b = vec4(v2,v4); //两个变量拼成一个变量，第一个变量取全部的值，第二个变量取剩下的值填满vec4

**注：**如果向构造函数中只传一个参数，构造函数会自动将这个参数赋值所有元素，但是如果给构造函数传了不止一个值，但又比所需的参数个数少，就会报错。

赋值

使用等号(=)来对矢量进行赋值操作。记住，赋值运算符左右两边的变量/值的类型必须一致，左右两边的元素个数也必须相同。赋值情况比较灵活，但大家可以自行尝试，体会下面代码的含义。

vec3 v3 = vec3(1.0,1.2,1.5); //三维矢量v3的设置为(1.0,1.2,1.5),即v3的三个分量x、y、z分别是1.0,1.2,1.5
vec2 v2 = vec2(v3); //使用三维矢量v3赋值给二维矢量v2，实际是使用v3的前两个元素给v2赋值
vec4 v4 = vec4(1.0); //将四位矢量v4设置为(1.0,1.0,1.0,1.0)
vev4 v4b = vec4(v2,v4); //使用v2和v4赋值v4b，结果为(1.0,1.2,1.0,1.0)

取值

矢量既可以通过点运算符(.)来访问也可以通过方括号运算符([])来访问。通常矢量通过点运算符来访问，只需要在矢量变量名后接点运算符，然后在接上分量名。

x,y,z,w 	用来获取顶点坐标的分量 
r,g,b,a 	用来获取颜色分量 
s,t,p,q 	用来获取纹理坐标的分量 

矢量可以用来存储顶点坐标、颜色和纹理坐标。所以GLSL ES支持以上三种分量名，这样大家在使用的时候便于理解，实际上，一个矢量的x分量或r分量还是s分量都会返回这个矢量的第1个分量，一个矢量的y分量或g分量还是t分量都会返回这个矢量的第2个分量。

**注:**这点实际上和咱们前端javascript很类似哈。这块需要大家留意的是需要多个分量搭配使用的方法，进行灵活运用

矢量常见用法

向量长度

$$\left|a\right|=\sqrt{x^2+y^2+z^2}$$

所谓的向量长度就是向量长度，你们懂的。是不是有点“听君一席话，胜似一席话”。开个玩笑，向量的长度应该就是它的模长，那它的模长又是何物呢，就是他的对应的线段长度。（不严谨哈，更加严谨的定义肯定得去查阅数学课本），上式子实际上是用代数式子表示模的长度。

向量归一化===单位向量

向量的大小（长度）称为向量的模（norm），一般记作
$$\mid A\mid =\sqrt{x^2+y^2}//shader中用法：length()$$
单位向量（Unit vector）指的是模为1的向量。单位向量的计算公式为：
$$\hat{a}=\frac{\vec{a}}{\mid \vec{a}\mid }$$
单位向量的长度为 1，一般只用来表示方向。

注：shader中用法：normalize()

向量加法与减法

向量的求和可以用两种法则：平行四边形法则或者三角形法则。

在代数上，对于在笛卡尔坐标系中定义的向量，向量求和可以简化为求向量各个对应坐标值的和。

**注：**shader中用法：vec2 f +=vec2 (1.,1.)

4.向量乘法

1）点乘（Dot product），又称为向量的内积。计算公式为：
$$\vec{a}.\vec{b}=\mid \vec{a}\mid \mid \vec{b}\mid cos\theta$$
代数形式如下所示：

点乘满足交换律以及分配律。
$$\vec{a}.\vec{b}=\vec{b}.\vec{a}$$

$$\vec{a}.(\vec{b}+\vec{c})=\vec{a}.\vec{b}+\vec{a}.\vec{c}$$

**注：**shader中用法：float f =dot(vec2 (0.,2.),vec2 (0.,1.))

实际应用

（1）计算两个向量夹角
$$\cos \theta =\frac{\vec{a}.\vec{b}}{\mid \vec{a}\mid \mid \vec{b}\mid }$$

$$\cos \theta =\hat{a}.\hat{b}$$

（2）计算一个向量到另一个向量上的投影 ，向量b在向量a上的投影满足，注意此时的投影是个标量

下面这个是根据三角形定则来的，得到的值是下面公式：
$$k=|\vec{b}|\cos \theta$$
再把上面公式的cos角度置换了，得到结果如下所示
$$k=\frac{\vec{a}.\vec{b}}{\mid \vec{a}\mid }$$

2）叉乘（Crossproduct），又称作向量的外积。两个向量叉乘的结果还是一个向量，这个向量和原来的两个向量垂直。叉乘的结果向量的长度为：
$$\Vert a\times b\Vert =\Vert a\mid \Vert b\Vert \sin \varphi$$
如果代数上表示的话如下公式所示：

几何意义

在几何中，叉积得到的向量与a和b所在平面垂直，长度等于向量a和b组成的平行四边形的面积，该向量被称为法向量。如图：

法向量方向：使用右手定则，首先伸出右手，并竖起大拇指，并将其余的四个手指握紧。以最小角度旋转向量a，使其与向量b的方向一致，四个手指朝向如上图，大拇指所指的方向就是法向量的方向。

**注：**shader中用法：vec2 f =cross (vec2 (.1,.2,.3 ),vec2 (.3,.2,.1))

矩阵

矩阵定义

矩阵（Matrix）是一个按照长方阵列排列的复数或实数集合 ，最早来自于方程组的系数及常数所构成的方阵。这一概念由19世纪英国数学家凯利首先提出。
GLSL ES支持矩阵类型，这种数据类型适合用来处理计算机图形。矩阵类型的变量包含多个元素，每个元素是一个数值（整型数、浮点数或布尔值)。矩阵将这些元素划分成行和列，可以用来表示变换矩阵。

矩阵类型介绍

GLSL ES常见矩阵类型如下所示：

mat2	2×2 的浮点数矩阵
mat3	3×3 的浮点数矩阵
mat4	4×4 的浮点数矩阵

行主序和列主序

在学习矩阵构造和赋值前先搞明白两个概念，按行主序和按列主序。WebGL中矩阵元素是按列主序存储在数组中的。

在WebGL中使用的矩阵都是按列主序的，例如你用构造函数创建一个4×4的矩阵时，向矩阵构造函数中传入矩阵的每一个元素的数值来构造矩阵，注意传入值的顺序必须是列主序的。

左乘

右乘

矩阵构造、赋值与取值

构造

创建普通的矩阵

mat4 mat44 = mat4(
    1.0, 2.0, 3.0, 4.0,
    5.0, 6.0, 7.0, 8.0,
    9.0, 10.0, 11.0, 12.0,
    13.0, 14.0, 15.0, 16.0
);

创建对角矩阵或者单位矩阵

mat4 matrix = mat4(1.0)
// 1.0 0.0 0.0 0.0
// 0.0 1.0 0.0 0.0
// 0.0 0.0 1.0 0.0
// 0.0 0.0 0.0 1.0

取值

mat4 mat44 = mat4(
    1.0, 2.0, 3.0, 4.0,
    5.0, 6.0, 7.0, 8.0,
    9.0, 10.0, 11.0, 12.0,
    13.0, 14.0, 15.0, 16.0
);

// 访问矩阵matrix44的第二列vec4 v4 = matrix44[1];//返回值vec4(5.0, 6.0, 7.0, 8.0,)

// 访问矩阵matrix44的第二列第一行对应的元素float f = matrix44[1][0];//返回5.0

矩阵常见用法

矩阵和浮点数相乘

mat4 mat44 = mat4(
    1.0, 2.0, 3.0, 4.0,
    5.0, 6.0, 7.0, 8.0,
    9.0, 10.0, 11.0, 12.0,
    13.0, 14.0, 15.0, 16.0
);
mat4 m44 = matrix44*10.;
//结果是
mat4 m44 = mat4(
    10.0, 20.0, 30.0, 40.0,
    50.0, 60.0, 70.0, 80.0,
    90.0, 100.0, 110.0, 120.0,
    130.0, 140.0, 150.0, 160.0
);

矩阵与点或（矢量）相乘

//声明一个点
vec4 point = vec4(0.,1.,1.,1.);
//向量扩大3倍
//3   0   0    0            0.
//0   3   0    0            1.
//0   0   3    0            1.
//0   0   0    1            1.
mat4 m44 = mat4(3,0,0,0,  0,3,0,0,  0,0,3,0,  0,0,0,1);
vec4 newPoint = m44*point ;
//平移后结果：newPos = vec4(0.,3.,3.,1.)

矩阵和矩阵相乘

1、当矩阵A的列数（column）等于矩阵B的行数（row）时，A与B可以相乘。

2、矩阵C的行数等于矩阵A的行数，C的列数等于B的列数。

3、乘积C的第m行第n列的元素等于矩阵A的第m行的元素与矩阵B的第n列对应元素乘积之和。

结构体定义

着色器中的机构体类似于我们其他语言中的类，GLSL的结构体可以组合基本类型和数组来形成用户自定义的类型。在定义结构体的时候，你可以直接定义一个结构体实例，或者在后面定义结构体实例。

方法一：

struct Light{
  vec3 position;//光源位置
  vec4 color;//光源颜色
}; light1，light2
// Light light1=Light(vec3(1.,2.,3.),vec4(8.,2.,4.,1.));

结构体访问与使用

1、=为结构体赋值，

2、==，!=来判断两个结构体是否相等。只有结构体中的每个成分都相等，那么这两个结构体才是相等的。

3、访问结构体的内部成员使用. (点语法)来访问。

4、固定大小的数组也可以被包含在结构体中。GLSL的结构体不支持嵌套定义。只有预先声明的结构体可以嵌套其中。

结构体注意事项

1、GLSL的结构体不支持嵌套定义，只有预先声明的结构体才可以嵌套其中。

2、结构体定义后面一定要加分号。

3、结构体定义是和main函数并列的。

4、结构体至少包含一个成员。

struct theTemp
{
    float pointSize;
    myTemp temp;
    //注意，这里是不合法的，不可以这么写。结构体只有预先定义过的才可以嵌套。
    struct cantUse{
        float a;
        float b;
    }test;
    //这也是个结构体，但是我们是在这个结构体的下面定义的，所以也是不合法的。
    subTemp sub;
}
struct subTemp
{
    float c;
    float d;
}tex;

数组

数组定义

在GLSL中，可以像C一样声明和访问数组，只支持一维数组，下标不能为负。

//声明含有4个数浮点数的数组 
float Array1[4];
//声明含2个vec4的对象数组
 vec4 Array2[2];

注意：

1、整型字面量

2、数组的长度必须大于 0；

3、数组前面定义的是每个子量的类型

数组构造、赋值与取值

只有整型常量表达式和uniform变量可以被用作数组的索引值。此外，与javascript或C不同，数组不能在声明时被一次性地初始化，而必须显式地对每个元素进行初始化。如下所示：

vec4 Array[0] = vec4(4.0, 5.0, 6.0, 1.0);    
vec4 Array[1] = vec4(3.0, 2.0, 0.0, 1.0);

数组元素可以通过索引值来访问，和JS等语言一样，索引值也是从0开始的。比如，下面这句代码就可以访问float Array变量的第3个元素：

float aa = Array[2];

数组运算

数组本身只支持[ ]运算符，但数组元素能够参与其自身类型支持的任意运算，如下：

//将floatArray的第2个元素乘以3.14    float f = Array[1] * 3.14    

//将vec4Array的第1个元素乘以vec4    vec4 v4 = vec4Array[0] * vec4(1.0, 2.0, 3.0, 4.0); 

限定词

GLSL ES 中提供了三类限定词，主要是为了提高运行效率，减少内存开销。

参数限定词—控制参数的行为
存储限定词—限定变量的类型
精度限定词—限定数据的精度

参数限定词

参数限定词顾名思义就是来限制函数参数的，根据参数不同的行为可以将它们分为以下几类：

● 只向函数中传值
● 在函数中被赋值
● 既向函数中传值也在函数中被赋值

存储限定词

存储限定词其实就是我们用来向着色器传值的变量类型，GLSL ES提供了attribute、uniform和varying三个限定词来声明特定用途的变量。

GLSL ES支持的存储限定词最大最小个数

attribute变量

attribute变量只能出现在顶点着色器中，只能被声明为全局变量，被用来表示逐顶点的信息。顶点着色器中能够容纳的attribute变量的最大数目与设备有关，你可以通过访问内置的全局常量来获取该值（最大数目)，支持WebGL 的环境都支持至少8个attribute变量。

uniform变量

uniform变量可以用在顶点着色器和片元着色器中，且必须是全局变量。uniform变量是只读的，不支持数组和结构体类型。

varying变量

varying限定词声明的变量也要求是全局变量，它担任着一个很重要的角色，就是从顶点着色器向片元着色器传值，

精度限定词

GLSL ES新引入了精度限定字,目的是帮助着色器程序提高运行效率,削减内存开支。 精度默认值写法:

#ifdef GL_ES
precision mediump float;
#endif

WebGL程序支持三种精度，限定词分别是 highp、mediump和lowp

通常会使用 precision 关键字为某一类型的变量设置默认精度，这个设置必须放置在程序的顶部。使用方式如下： $$precision<精度限定词><类型名称>$$ 默认精度限定参照表：

函数

函数结构

GLSL ES 的函数定义与C语言接近，基本构成包括返回类型、函数名、参数和函数体，若无返回值，需要使用 void 代替。具体结构如下 ：

返回类型 函数名 (type0 arg0, type1 arg1, ...,typen argn) {
    函数计算
    return 返回值;
}

参数的type必须为本章所述的类型之一，或者像main()函数这样没有参数也是允许的。如果函数不返回值，那么函数中就不需要有return语句。但这种情况下，返回类型必须是void。你也可以将自己定义的结构体类型指定为返回类型，但是结构体的成员中不能有数组。

注：使用函数时传入的参数类型必须与声明函数时指定的参数类型一致。在GLSL中函数不能在函数内部调用它本身，也就是说不允许递归调用，这项限制的目的是为便于编译器对函数进行内联展开。

规范声明

与C语言一样，如果函数定义在其调用之后，那么必须在进行调用前先声明该函数的规范，规范声明预先告诉GLSL系统函数的参数、参数类型、返回值等信息。

流程控制

着色器中的流程控制与C和JavaScript语言中的流程控制几乎无异，主要是通过if语句和for语句等控制流程。

if语句

if语句有三种控制流程的语句模型，分别是 if 模型、 if…else… 模型 和 if…else if…else 模型。

if(条件表达式1){
    如果条件表达式1为true，执行这里。
} else if(条件表达式2)
{
    如果条件表达式1为false而条件表达式2为true，执行这里。
} else {
    如果上述两个条件都为false执行这里。
}

注：if语句或if-else语句中都必须包含一个布尔值，或者是产生布尔值的表达式。此处不可以使用布尔值类型矢量,比如bvec2。GLSL ES中没有switch语句，在程序中避免过多的使用if语句，否则会影响效率

for语句

大多数循环程序都是通过for语句实现的，GLSL ES 语言也一样，for 语句的格式如下:

for (初始化表达式;条件表达式;循环步进表达式){
    重复执行的语句;
}

GLSL ES 语言的for循环的循环变量有一些特殊的限制，具体如下:

● 一个for循环中只允许有一个循环变量，且只能是int类型或float类型；

● 循环步进表达式必须是以下的形式中的一种，i++，i–，i+=常量表达式，i-=常量表达式；

● 条件表达式必须是循环变量与整形常量的比较；

● 循环体内，循环变量不可以被赋值。

continue、break语句

通常情况下，我们会在for语句中使用continue语句来跳过本次循环，使用break语句终止循环。

continue： 中止包含该语句的最内层循环和执行循环表达式(递增/递减循环变量)，然后执行下一次循环。

break：中止包含该语句的最内层循环，并不再继续执行循环。

discard语句

discard语句只能在片元着色器中使用，表示放弃当前片元直接处理下一个片元，作用与continue类似。

预处理

预处理指令用来在着色器程序真正编译之前对代码进行预处理，预处理指令都是以 (#) 开始。当我们编写 GLSL 代码时，编译器需要先对代码进行处理，然后才能将其编译成机器可以执行的指令。预处理指令就是在这个处理过程中对代码进行一些操作。

#define

使用 #define 指令定义常量，可以在代码中使用该常量来提高代码的可读性和维护性。

#ifdef, #ifndef, #else, #elif, #endif

根据不同的条件选择编译不同的代码。这样可以让代码更加灵活，便于开发人员进行调试和测试。

#version

指定当前代码所使用的 GLSL 版本，确保代码与特定版本的 GLSL 兼容。必须在着色器顶部，在它之前只能有注释和空白。

#warning 和 #error

在编译期间生成警告和错误信息，帮助开发人员调试和诊断代码问题。

#extension

预处理指令中另一个非常重要的是 #extension，用来控制是否启用某些扩展的功能。

#extension extension_name : enable/disable

预处理指令可以让我们更好地组织代码，提高代码的可读性和可维护性，同时也能够帮助我们调试和诊断代码问题。

WebGL Shader内置变量和常量

内置变量

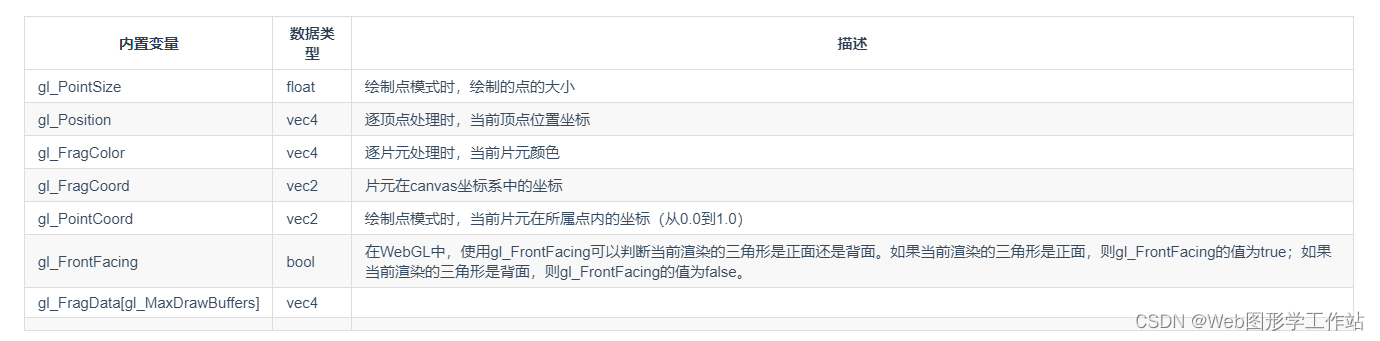
内置常量

OpenGL OpenGL ES WebGL GLSL 版本

GLSL ES 是用于在 WebGL 中编写顶点和片段着色器代码的语言。WebGL2.0支持较新版本的GLSL，称为GLSL3，而WebGL1.0仅支持GLSL1。GLSL3 提供了以前 GLSL1 不支持的新类型、运算符和函数，并且用于从着色器程序导入、导出数据的语法略有不同。

注：webgl里面读取版本的方式是：

  console.log(`${gl.getParameter(gl.VERSION)}与${gl.getParameter(gl.SHADING_LANGUAGE_VERSION)}`);

GLSL ES版本差异

版本 100

顶点着色器
#version 100 es
uniform mat4 projTrans;
attribute vec2 Position;
attribute vec2 TexCoord;
varying vec2 vTexCoord;

void main() {
    vTexCoord = TexCoord;
    gl_Position = u_projView * vec4(Position, 0.0, 1.0);
}
片段着色器
#version 100
uniform sampler2D tex0;
varying vec2 vTexCoord;
void main() {
    vec4 color = texture2D(tex0, vTexCoord);
    gl_FragColor = color;
}

版本 300

顶点着色器

#version 300 es
in vec4 a_position;
uniform vec4 u_offset;
 out vec4 v_positionWithOffset;
 void main() {
  gl_Position = a_position + u_offset;
  v_positionWithOffset = a_position + u_offset;
}

片段着色器
#version 300 es
precision highp float;
in vec4 v_positionWithOffset;
out vec4 outColor;
void main() {
 vec4 color = v_positionWithOffset * 0.5 + 0.5;
  outColor = color;
}

参考地址：https://registry.khronos.org/OpenGL/index_es.php#specs32

小结

章节复习

现在我们来检验你对这结课程的理解？

• 手写两个矩阵相乘

A = [[1, 2, 3],
     [4, 5, 6]]

B = [[7, 8],
     [9, 10],
     [11, 12]]
C = [[58, 64],
     [139, 154]]