【张量｜RTCTV】enhanced low-rank tensor recovery fusing reweight【融合重加权张量相关总变分正则化的增强低秩张量恢复方法用于图像去噪】】

Q&A

• 重加权是什么

  重加权（Reweighted）

  重加权技术是一种在优化问题中增强模型性能的方法，特别是在处理稀疏性和低秩性问题时应用广泛。以下是重加权技术的详细解释：

  1. 重加权的基本概念

  重加权技术通过迭代地调整权重，逐步逼近目标函数的理想解。它通过对目标函数中某些部分赋予不同的权重，来更准确地描述数据的特性。例如，在低秩矩阵恢复或稀疏信号重建中，重加权技术可以更有效地突出重要特征，同时抑制噪声和不重要的特征。

  2. 重加权核范数

  在低秩矩阵恢复中，常用的核范数 $\Vert X{\Vert }_{\ast }$ 计算矩阵 $X$ 的奇异值之和。然而，直接使用核范数会对所有奇异值等同对待，无法区分重要和不重要的奇异值。重加权核范数通过对奇异值应用不同的权重，更灵活地控制低秩性：

  $$\Vert X{\Vert }_{w,\ast }=\sum _i{w}_i{\sigma }_i(X)$$

  其中：

  • ${\sigma }_i(X)$ 是矩阵 $X$ 的第 $i$ 个奇异值。
  • $w_i$ 是对应的权重，通常定义为： $w_i={\frac{c}{{\sigma }_i(X)+ϵ}}^{1-p}$ ，其中 $c$ 和 $ϵ$ 是常数，$0<p\le 1$。

  这种重加权策略使得较大的奇异值受到较小的惩罚，而较小的奇异值受到较大的惩罚，从而更有效地抑制噪声。

  3. 重加权总变差

  在图像去噪中，总变差（TV）正则化用于保持图像的局部平滑性。重加权总变差通过对梯度的奇异值赋予不同权重，进一步提高了去噪性能：

  $$\Vert X{\Vert }_{RTCTV}=\sum _{k=1}^3{\alpha }_k\Vert G_k{\Vert }_{w,\ast }$$

  其中：

  • ${\alpha }_k$ 是权重参数，控制不同方向梯度的权重。

  • $G_k$ 是梯度张量。

  • $\Vert G_k{\Vert }_{w,\ast }$ 是梯度张量的重加权核范数，定义为：

    $$\Vert G_k{\Vert }_{w,\ast }=\frac{1}{n_3}\sum _{i=1}^{n_3}\sum _{j=1}^{\min (n_1,n_2)}{w}_{ij}{\sigma }_j(G_L^{(i)})$$

  4. 重加权策略的迭代过程

  重加权方法通常通过迭代过程实现。在每次迭代中，根据当前解的特性调整权重，从而逐步逼近目标函数的最优解。具体步骤如下：

  1. 初始化权重：根据初始解（如观测图像）设置初始权重。
  2. 优化求解：使用当前权重进行优化，求解更新后的解。
  3. 更新权重：根据更新后的解调整权重，通常是降低较大奇异值的权重，增加较小奇异值的权重。
  4. 迭代收敛：重复步骤2和3，直到解收敛或达到预定的迭代次数。

  例子

  在图像去噪中，使用重加权技术可以显著提升去噪效果。以下是一个简单的重加权迭代过程：

  1. 初始化：设定初始权重 $w^{(0)}$。
  2. 迭代：
     • 用当前权重 $w^{(t)}$ 进行去噪，求解当前图像 $X^{(t+1)}$。
     • 更新权重：$w_i^{(t+1)}={\frac{c}{{\sigma }_i(X^{(t+1)})+ϵ}}^{1-p}$。
  3. 检查收敛条件，若满足则停止，否则继续迭代。

  通过以上过程，可以逐步减少噪声的影响，提高图像的去噪效果。

• Fig.1 解释

  

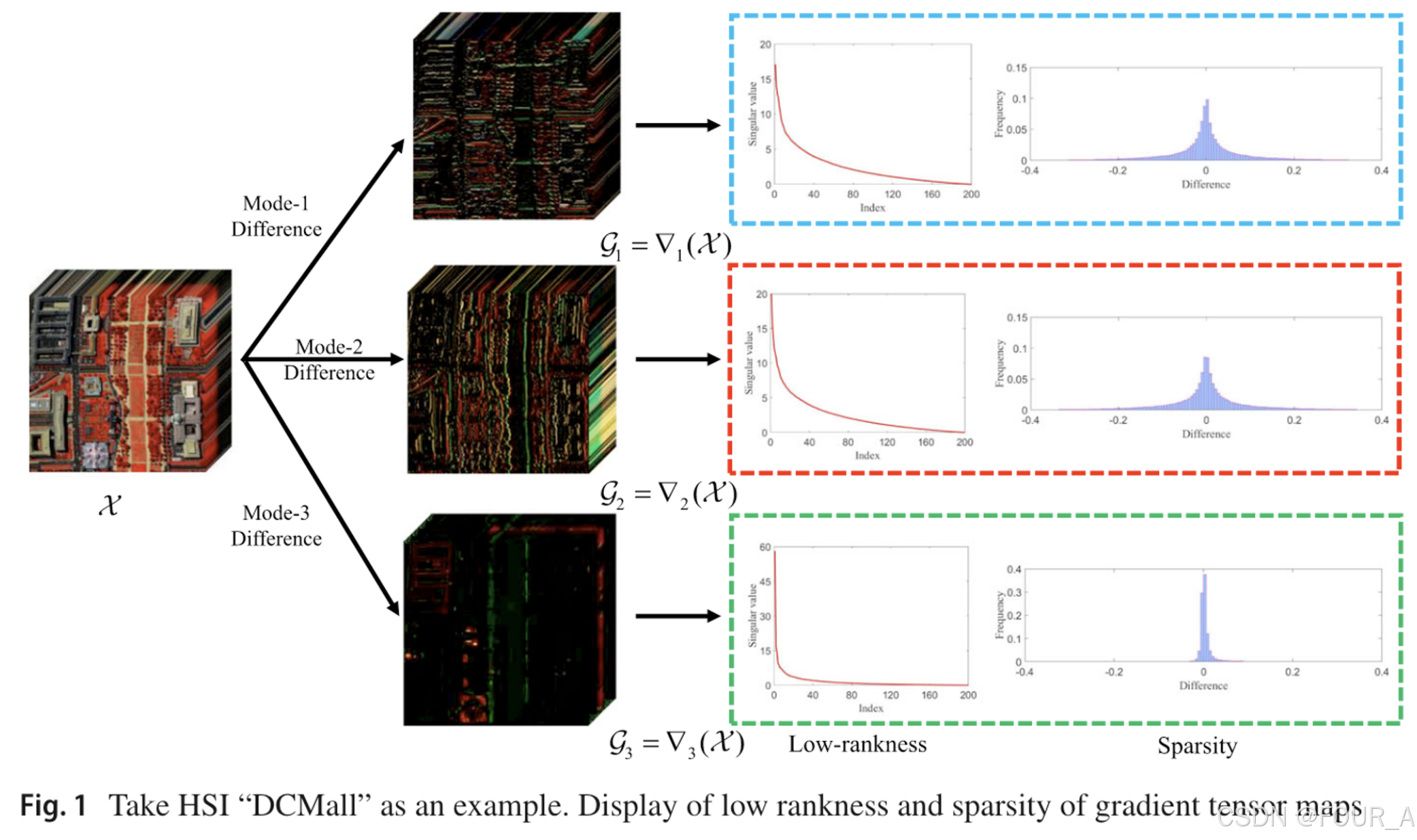
  这张图展示了张量数据的不同模式上的梯度差分，以及这些差分的低秩性和稀疏性的表现。以下是对这张图的详细解释：

  图的结构和内容

  1. 左侧的原始张量 $\mathcal{X}$：
     • 这个张量表示一个高光谱图像（HSI），图中示例为“DCMall”。
     • 张量的每一个维度（模式）可以分别表示图像的不同维度，比如宽度、高度和光谱带。
  2. 中间的梯度差分：
     • 图中展示了在三个模式上的梯度差分：
       • Mode-1 Difference：表示在模式1（例如图像宽度）上的差分，结果为张量 ${\nabla }_1(\mathcal{X})$
       • Mode-2 Difference：表示在模式2（例如图像高度）上的差分，结果为张量 ${\nabla }_2(\mathcal{X})$
       • Mode-3 Difference：表示在模式3（例如光谱带）上的差分，结果为张量 ${\nabla }_3(\mathcal{X})$
  3. 右侧的低秩性和稀疏性分析：
     • 每个梯度差分张量对应两个图：
       • 低秩性（Low-rankness）：左侧的图显示了对应张量的奇异值曲线。这条曲线展示了张量的奇异值从大到小的分布情况。通常，快速下降的奇异值曲线表明张量具有低秩性。
       • 稀疏性（Sparsity）：右侧的图显示了梯度差分张量元素的直方图。集中于零附近的直方图表明这些梯度张量具有稀疏性。

  总结

  这张图通过展示原始张量 $\mathcal{X}$ 的各个模式上的梯度差分，结合这些差分张量的奇异值曲线和元素分布直方图，直观地表明了这些梯度张量在各个模式上的低秩性和稀疏性。这种低秩性和稀疏性是使用TCTV（Tensor Correlated Total Variation）方法进行张量恢复的理论基础。

融合重加权张量相关总变分正则化的增强低秩张量恢复方法用于图像去噪

初步分析

摘要

这篇论文提出了一种新的图像去噪方法，名为重加权张量相关总变分（RTCTV）正则化方法。此方法利用图像梯度张量的内在结构特性，通过重加权策略来区分处理不同的奇异值，从而更好地描述图像的全局低秩性和局部光滑性。为了解决所提出的模型，论文设计了一种基于交替方向乘子法（ADMM）的算法。广泛的实验结果表明，该方法在多种视觉张量数据上的去噪效果优于现有的图像去噪方法。

动机

当前：

方法：利用图像的全局低秩性和局部光滑性先验信息来建模

缺点：参数调优繁琐和无法灵活处理实际问题等局限性

本文：

方法：融合重加权策略的张量相关总变分正则化方法

优点：服这些问题并提高图像去噪性能

贡献

1. 提出了重加权张量相关总变分（RTCTV）正则化方法，同时描述图像的全局低秩性和局部光滑性。
2. 设计了一种新的图像去噪模型，该模型不需要调整TV正则化项的参数，只需调整噪声正则化项和权重参数。
3. 设计了基于ADMM的算法来求解所提出的模型，并在多个类型的视觉张量数据上进行了广泛的实验验证，结果表明该方法在评价指标和视觉效果上均优于现有的图像去噪方法。

方法

1. 重加权张量相关总变分正则化

RTCTV 正则化方法通过重加权策略对梯度张量的不同奇异值进行差异化处理，更好地描述了梯度张量的低秩性和固有稀疏性。具体公式如下：

$$\Vert X{\Vert }_{\text{RTCTV}}=\sum _{k=1}^3{\alpha }_k\Vert {\mathcal{G}}_k{\Vert }_{w,\ast ,L}$$

其中，${\alpha }_k$ 代表对应模式的权重参数，$\Vert G_k{\Vert }_{w,\ast ,L}$ 为重加权核范数。

2. 图像去噪模型

本文提出的 RTCTV 图像去噪模型结合了全局低秩性和局部光滑性先验信息，并通过重加权策略进一步提高了模型的灵活性。具体模型如下：

$$
\min_{X, \mathcal{G}k, E, N} \sum{k=1}^3 \alpha_k |\mathcal{G}k|{w,*,L} + \lambda |E|_1 + \beta |N|_2^2

$$

$$\text{s.t.}M=X+E+N,{\mathcal{G}}_k={\nabla }_k(X)$$

其中，$M$ 为观测图像，$X$ 为去噪后的图像，$E$ 和 $N$ 分别为稀疏噪声项和高斯噪声项。

3. 解决算法

利用 ADMM 算法来求解 RTCTV 模型。具体步骤包括：

1. 更新 $X$：通过傅里叶域中的卷积定理求解优化子问题。
2. 更新 $G_k$：利用之前定义的 t-WSVT 阈值算子进行更新。
3. 更新 $E$：使用张量软阈值算子进行更新。
4. 更新 $N$：通过优化子问题的导数求解。
5. 更新乘子 ${\lambda }_k$ 和 ${\beta }_k$。

实验

在高光谱图像（HSI）、多光谱图像（MSI）、彩色图像、灰度视频和CT图像等多种视觉张量数据上进行了广泛的去噪实验。实验结果表明，与其他图像去噪方法相比，所提出的RTCTV方法在去噪性能和视觉效果上均表现出显著优势。

实验结果示例

• HSI 数据：在多种噪声条件下，RTCTV 方法显著优于LRMR、KBR、LRTV等现有方法。
• MSI 数据：在不同噪声条件下，RTCTV 方法仍表现出较好的去噪效果，尽管其优势在带数较少的数据上略显不足。
• 其他视觉数据：在彩色图像、灰度视频和CT图像上，RTCTV方法展示了强大的噪声去除能力。

结论

本文提出的RTCTV方法通过融合全局低秩性和局部光滑性先验信息，并利用重加权策略对梯度张量的不同奇异值进行差异化处理，显著提高了图像去噪的性能。广泛的实验验证了该方法的有效性和优越性，为实际应用中的图像去噪问题提供了一个强有力的解决方案。

---

3.3 RTCTV 正则化

目标：通过引入重加权张量相关全变差（Reweighted Tensor Correlated Total Variation，RTCTV）范数来增强张量相关全变差（TCTV）范数的灵活性。

关键组成部分和定义

1. RTCTV 范数：

   • 定义为：

     $$\Vert X{\Vert }_{\text{RTCTV}}:=\sum _{k=1}^3{\alpha }_k\Vert {\mathcal{G}}_k{\Vert }_{w,\ast ,L}$$

   • 其中，${\alpha }_k$ 代表每个模式的权重参数，满足 ${\sum }_{k=1}^3{\alpha }_k=1$。

   • $\Vert \mathcal{G}{\Vert }_{w,\ast ,L}$ 是梯度张量 $\mathcal{G}$ 的重加权核范数。

2. 重加权核范数：

   • 对于梯度张量 $G$ 定义为：

     ∥ G ∥ w , ∗ , L = 1 n 3 ∑ i = 1 n 3 ∑ j = 1 min ⁡ { n 1 , n 2 } w i j σ j ( G L ( i ) ) \|\mathcal{G}\|_{w,*,L} = \frac{1}{n_3} \sum_{i=1}^{n_3} \sum_{j=1}^{\min\{n_1, n_2\}} w_{ij} \sigma_j (\mathcal{G}^{(i)}_L) ∥G∥w,∗,L​=n3​1​i=1∑n