回归分析（线性回归、逻辑回归）详解与 Python 实现

1. 回归分析概述

  回归分析是处理多变量间相关关系的一种数学方法。相关关系不同于函数关系，函数关系反应变量间严格依存性，简单说就是一个自变量对应一个因变量。而相关分析中，对自变量的每一个取值，因变量可以有多个数值与之对应。在统计上，研究相关关系可以运用 回归分析 和 相关分析。
  当自变量为非随机变量而因变量为随机变量时，它们的关系分析成为 回归分析。当自变量和因变量都是随机变量时，它们的关系分析称为 相关分析。回归分析和相关分析往往不加区分。广义上说，相关分析包括回归分析，但是严格说两者是有区别的。
  具有相关关系的两个变量 ξ 和 η（ξ：克西、η ：伊塔 ），它们之间虽然存在着密切的关系，但不能由一个变量精确地求出另一个变量的值。通常选用 ξ = x 时 η 的数学期望作为对应 ξ = x 时 η 的代表值，因此它反映 ξ = x 条件下 η 取值的平均水平。这样的对应关系称为 回归关系。根据回归分析可以建立变量间的数学表达式，称为 回归方程。回归方程反映自变量在固定条件下因变量的平均状态变化情况。
  具有相关关系的变量之间虽然具有某种不确定性，但是通过对现象的不断观察可以探索出它们之间的统计规律，这类统计规律称为 回归关系。有关回归关系理论、计算和分析称为 回归分析。
  回归分析可以分为 线性回归分析 和 逻辑回归分析。

2. 线性回归

线性回归就是将输入项分别乘以一些常量，再将结果加起来得到输出。线性回归包括一元线性回归和多远线性回归。

线性回归模型的优缺点

• 优点：快速；没有调节参数；可轻易解释；了理解。
• 缺点：相比其他复杂一些的模型，其预测准确率不高，因为它假设特征和响应之间存在确定的线性关系，这种假设对于非线性的关系，线性模型显然不能很好地进行数据建模。

2.1 简单线性回归分析

  线性回归分析中，如果仅有一个自变量与一个因变量，且其关系大致可以用一条直线表示，则称之为 简单线性回归分析。
  如果发现因变量 Y 和自变量 X 之间存在高度的正相关，则可以确定一条直线方程，使得所有的数据点尽可能接近这条拟合的直线。
$$Y=a+bx$$
  其中 $Y$ 为因变量，$a$ 为截距，$b$ 为相关系数，$x$ 为自变量。

2.2 多元线性回归分析

  多元线性回归分析是简单线性回归分析的推广，指的是多个因变量对多个自变量的回归分析。其中最常用的是只限于一个因变量但有多个自变量的情况，也叫做多重回归分析。
$$Y=a+b_1{X}_1+b_2{X}_2+b_3{X}_3+\cdots +b_k{X}_k$$
  其中，$a$ 代表截距，$b_1,b_2,b_3,\cdots ,b_k$ 为回归系数。

2.3 非线性回归数据分析

数据挖掘中常用的一些非线性回归模型：

1. 渐进回归模型
   $$Y=a+b{e}^{-rX}$$
2. 二次曲线模型
   $$Y=a+b_{1}X+b_2{X}^2$$
3. 双曲线模型
   $$Y=a+\frac{b}{X}$$

3. 用 python 实现一元线性回归

一个简单的线性回归的例子就是房子价值预测问题。一般来说，房子越大，房屋的价值越高。
  数据集：input_data.csv
  
  说明：
    No：编号
    square_feet：平方英尺
    price：价格（元/平方英尺）

代码如下：

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn import linear_model

# 读取数据的函数
def get_data(file_name):
    data = pd.read_csv(file_name)
    X = []
    Y = []
    for square_feet, price in zip(data["square_feet"],data["price"]):
        X.append([square_feet])
        Y.append(price)
    return X,Y

# 建立线性模型，并进行预测
def get_linear_model(X, Y, predict_value):
    model = linear_model.LinearRegression().fit(X,Y)
    pre = model.predict(predict_value)
    predictions = {
   }
    predictions["intercept"] = model.intercept_  # 截距值   
    predictions["coefficient"] = model.coef_     # 回归系数（斜率）
    predictions["predictted_value"] = pre
    return predictions

# 显示线性拟合模型结果
def show_linear_line(X,Y):
    model = linear_model.LinearRegression().fit(X,Y)
    plt.scatter(X,Y)
    plt.plot(X,model.predict(X),color="red")
    plt.title("Prediction of House")
    plt.xlabel("square feet")
    plt.ylabel("price")
    plt.show()  

# 定义主函数
def main():
    X, Y = get_data("input_data.csv")
    print("X:",X)
    print("Y:",Y)
    predictions = get_linear_model(X,Y,[[700]])
    print(predictions)
    show_linear_line(X,Y)
    
main()

结果截图：

4. 用 python 实现多元线性回归

  当结果值影响因素有多个时，可以采用多元线性回归模型。例如：商品的销售额可能与电视广告投入、收音机广告投入和报纸广告投入有关系，可以有：
$$Sales={\beta }_0+{\beta }_{1}TV+{\beta }_{2}Radio+{\beta }_{3}Newspaper$$
数据集：Advertising.csv

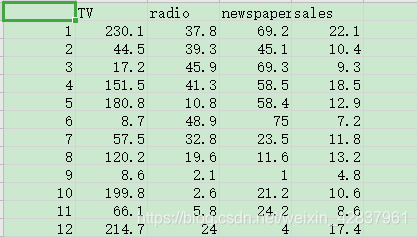
代码如下：

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import explained_variance_score,\
mean_absolute_error,mean_squared_error,median_absolute_error,r2_score

# 1.读取数据
data = pd.read_csv("Advertising.csv")
print(data.head())
print("shape:",data.shape)


# 2.分析数据
sns.pairplot(data, x_vars=["TV","radio","newspaper"], y_vars="sales",height=5,aspect=0.8,kind="reg")
plt.show()


# 3.建立线性回归模型

# （1）使用 pandas 构建 X（特征向量）和 y（标签列）
feature_cols = ["TV","radio","newspaper"]
X = data[feature_cols]
y = data["sales"]

# （2）构建训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X,y,random_state=1)  # 25% 测试

# （3）构建线性回归模型并训练
model = LinearRegression().fit(X_train,y_train)

# （4）输出模型结果
print("截距：",model.intercept_)
coef = zip(feature_cols, model.coef_)
print("回归系数：",list(coef))


# 4. 预测
y_pred = model.predict(X_test)


# 5. 评价
# 这个是自己写函数计算
sum_mean = 0
for i in range(len(y_pred)):
    sum_mean += (y_pred[i] - y_test.values[i])**2
sum_erro = np.sqrt(sum_mean/len(y_test))
print("均方根误差（RMSE）：",sum_erro)

# 这个是调用已有函数,以后就直接用
print("平均绝对误差（MAE）：",mean_absolute_error(y_test,y_pred))
print("均方误差（MSE）：",mean_squared_error(y_test,y_pred))
print("中值绝对误差：",median_absolute_error(y_test,y_pred))
print("可解释方差：",explained_variance_score(y_test,y_pred))
print("R方值：",r2_score(y_test,y_pred))

# 绘制 ROC 曲线
plt.plot(range(len(y_pred)),y_pred,"b",label="predict")
plt.plot(range(len(y_pred)),y_test,"r",label="test")
plt.xlabel("number of sales")
plt.ylabel("value of sales")
plt.legend(loc="upper right")
plt.show()

结果截图：

说明：

• pandas 两个主要的数据结构是 Series 和 DataFrame；Series 类似于一维数组，它由一组数据及一组与之有关的数据标签（及索引）组成；DataFrame 是一个表格型的数据结构，它含有一组有序的列，每列可以是不同的值类型。DataFrame 既有行索引也有列索引。
• 在分析数据时，使用了 seaborn 包，这个包数据可视化效果更好。其实 seaborn 包 也属于 Matplotlib 的内部包，只是需要单独安装。
• scikit-learn 要求 X 是一个特征矩阵，y 是一个 Numpy 向量。因此，X 可以是 pandas 的 DataFrame，y 可以是 pandas 的 Series。
• 对于分类问题，评价测度是准确率，但其不适用于回归问题，因此使用针对连续数值的评价测度（evaluation metrics）。
  
  

5. 逻辑回归

  逻辑回归也被称为广义线性回归模型，它与线性回归模型的形式基本上相同，最大的区别就在于它们的因变量不同，如果是连续的，就是多重线性回归；如果是二项分布，就是逻辑回归（Logistic）；逻辑回归实际上是一种分类方法，主要用于二分类问题（即输出只有两种，分别代表两个类别）。
  逻辑回归的过程：面对一个回归或者分类问题，建立代价函数，然后通过优化方法迭代求解出最优的模型参数，然后测试验证这个求解模型的好坏。

逻辑回归的优缺点

• 优点：速度快，适合二分类问题；简单。易于理解，可以直接看到各个特征的权重；能容易地更新模型吸收新的数据。
• 缺点：对数据和场景的适应能力有局限性，不如决策树算法强。

逻辑回归的常规步骤

1. 寻找 $h$ 函数（预测函数）
2. 构造 $J$ 函数（损失函数）
3. 想办法使 $J$ 函数最小并求得回归参数 （θ）

5.1 构造预测函数（假设函数）

  二类分类问题的概率与自变量之间的关系图形往往是一个 S 型曲线，采用 sigmoid 函数实现，函数形式：
$$g(z)=\frac{1}{1+e^{-z}}$$

  对于线性边界情况，边界形式如下：
$$z={\theta }^{T}x={\theta }_0{x}_0+{\theta }_1{x}_1+\cdots +{\theta }_n{x}_n=\sum _{i=0}^n{\theta }_i{x}_i$$
    说明：$(x_0,x_1,\dots ,x_n)$ 为输入数据的特征，$({\theta }_0,{\theta }_1,\dots ,{\theta }_n)$ 为回归系数，也可以理解为权重 $w$。

  最佳参数：
$$\theta =[{\theta }_0,{\theta }_1,{\theta }_2,\dots ,{\theta }_n{]}^T$$

  构造预测函数为：
h θ ( x ) = g ( θ T x ) = 1 1 + e − θ T x