蓝桥杯完美正方形【dfs】

最新推荐文章于 2021-05-07 23:52:18 发布

原创最新推荐文章于 2021-05-07 23:52:18 发布 · 521 阅读

2 ·

CC 4.0 BY-SA版权

Accept 专栏收录该内容

161 篇文章

订阅专栏

本文探讨了如何通过网格化和染色算法解决完美正方形拼接问题，使用C++实现了一个具体的解决方案，展示了如何避免正方形重叠并完全填充大正方形。

标题：完美正方形

如果一些边长互不相同的正方形，可以恰好拼出一个更大的正方形，则称其为完美正方形。

历史上，人们花了很久才找到了若干完美正方形。比如：如下边长的22个正方形
2 3 4 6 7 8 12 13 14 15 16 17 18 21 22 23 24 26 27 28 50 60
如【图1.png】那样组合，就是一种解法。

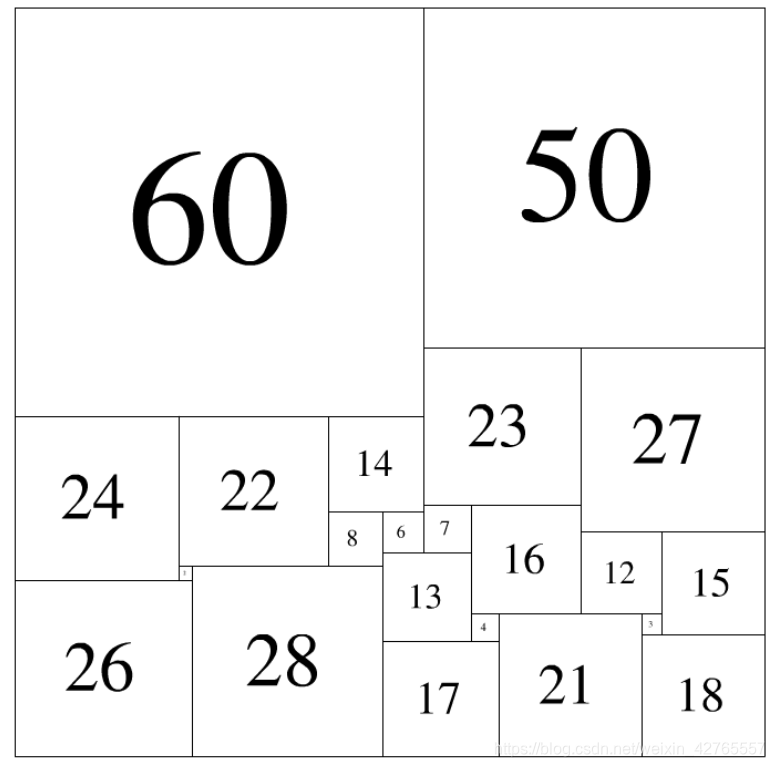
此时，紧贴上边沿的是：60 50
紧贴下边沿的是：26 28 17 21 18

22阶完美正方形一共有8种。下面的组合是另一种：
2 5 9 11 16 17 19 21 22 24 26 30 31 33 35 36 41 46 47 50 52 61
如果告诉你该方案紧贴着上边沿的是从左到右依次为：47 46 61，
你能计算出紧贴着下边沿的是哪几个正方形吗？

请提交紧贴着下边沿的正方形的边长，从左到右，用空格分开。

不要填写任何多余的内容或说明文字。

思路：
meshgrid ----，网格化（即50*50的正方形由50*50个像素点组成），然后就变成了染色问题~。在左上角摆47*47的正方形即把以(1,1)~(47,47)这些像素点染成颜色47。注意染过色的像素点不能二次染色，即一个正方形不能覆盖另一个正方形。恰好能将全部像素点染色，就是本题的解。

Code

#include <bits/stdc++.h>
using namespace std;
int a[] = {0,2,5,9,11,16,17,19,21,22,24,26,30,31,33,35,36,41,46,47,50,52,61};
int len,mp[201][201];
bool book[101];
bool Judge(int x,int y,int num)
{
	if(x+num-1 > len || y+num-1 > len)
		return false;
	for(int i=x;i<x+num;i++) 
		for(int j=y;j<y+num;j++)
			if(mp[i][j])
				return false;
	return true;
}
void color(int x,int y,int num)
{
	int l; 
	if(num == 0) {	
		book[mp[x][y]] = false;
		l = mp[x][y];
	}
	else {
		book[num] = true;
		l = num;
	} 
	for(int i=x;i<x+l;i++) 
		for(int j=y;j<y+l;j++)
			mp[i][j] = num;
}
bool flag;
void dfs(int x,int y)
{
	if(x == len+1) {
		flag = true;
		return ;
	}
	if(mp[x][y]) {
		if(y == len)
			dfs(x+1,1);
		else
			dfs(x,y+1);
		return;
	}
	for(int i=1;i<=22;i++) {
		if(book[a[i]])
			continue;
		if(!Judge(x,y,a[i]))
			break;	//a[i]随着i增大而增大,因此没必要在试下去
		color(x,y,a[i]);
		if(y == len)
			dfs(x+1,1);
		else
			dfs(x,y+1);
		if(flag)
			return;
		color(x,y,0);
	}

}
int main()
{
	len = 47+46+61;
	flag = false;
	memset(mp,0,sizeof mp);
	memset(book,false,sizeof book);

	color(1,1,47);
	color(1,1+47,46);
	color(1,1+47+46,61);
	
	dfs(1,1);
	
	int colorr=-1;
	for(int i=1;i<=len;i++) {
		if(mp[len][i] != colorr) {
			colorr = mp[len][i];
			printf("%d ",colorr);
		}
	}

	return 0;
}