【SLAM十四讲】第四讲

第三章讲了如何表示位姿，但实际位姿是未知的，需要估计，估计是有误差的，需要优化，进而将位姿估计问题转化为优化问题

总结图

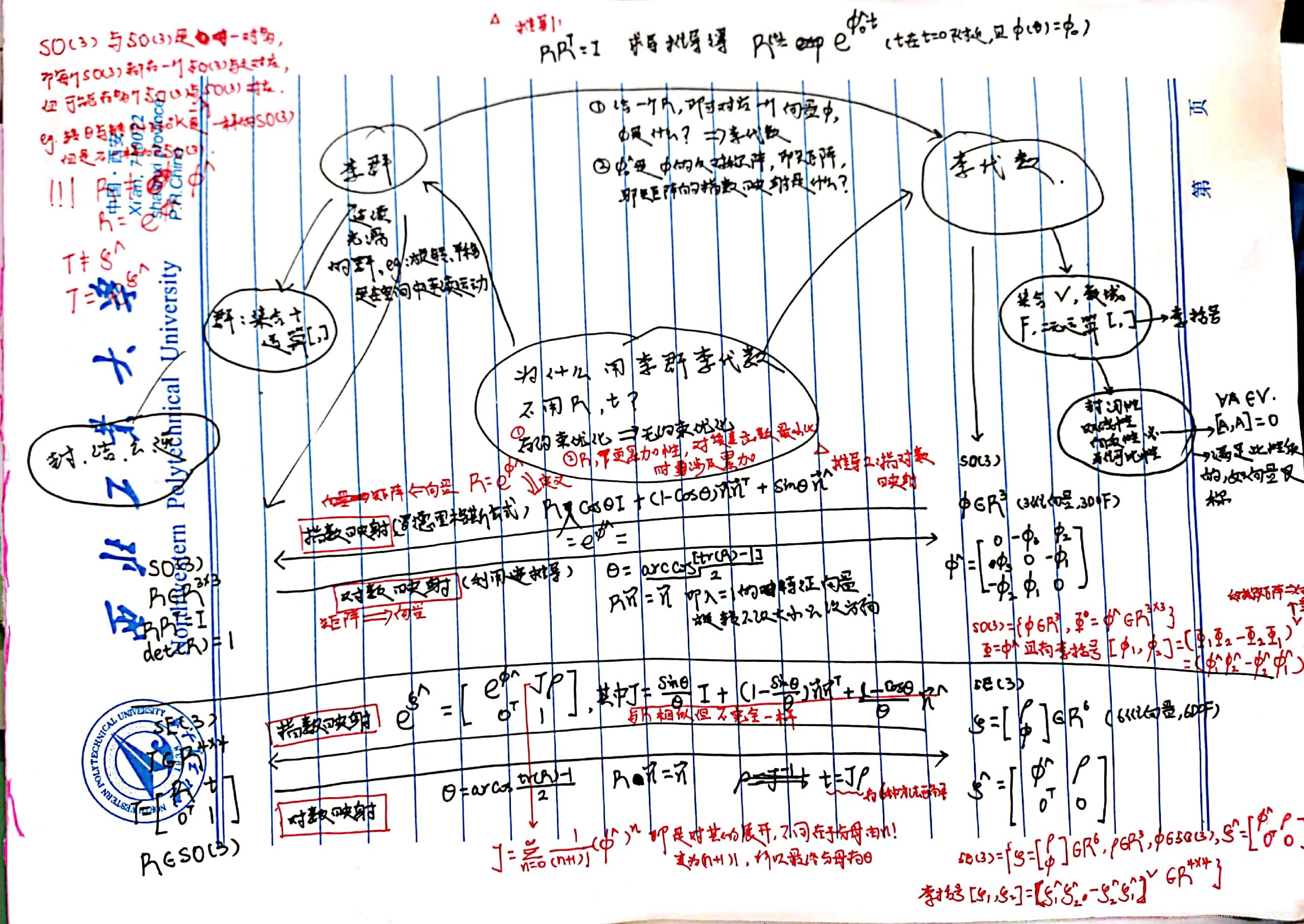
1.为什么需要李代数，不用R和t

1. 将有约束的优化转为无约束的：R是一个旋转矩阵，是正交阵且行列式为1，自身存在约束。
2. R和T只有累乘，没有累加性，但是很多损失函数也就是优化对象都是累加的

2.什么是群？什么是李群

1. 群：集合+运算
2. 满足性质：封，结，幺，逆
3. 一般线性群：GL，n*n的可逆矩阵，对乘法成群
   特殊正交群：SO，旋转矩阵
   特殊欧氏群：SE，n维欧式变换
   李群：具有连续光滑性质（可微）的群。SO和SE在实数空间（可以连续旋转），是李群。

3. 由李群引出李代数

R (t) = exp(φ^t)

即旋转矩阵是某个向量的反对称矩阵的