matlab小课堂04—最短路问题（固定起点）

一、固定起点的最短路

Dijstra算法

实例

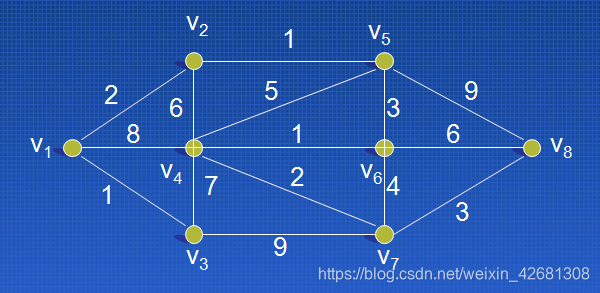
问题：

1. 求顶点V1到V8的最短路
2. 求顶点V1到其他各个顶点的最短路

步骤：

1. 写入图的赋权邻接矩阵（到自身结点的权为0，达不到的结点权为inf）
2. 利用Dijstra算法求解

结果：

w =

     0     2     1     8   Inf   Inf   Inf   Inf
     2     0   Inf     6     1   Inf   Inf   Inf
     1   Inf     0     7   Inf   Inf     9   Inf
     8     6     7     0     5     1     2   Inf
   Inf     1   Inf     5     0     3   Inf     9
   Inf   Inf   Inf     1     3     0     4     6
   Inf   Inf     9     2   Inf     4     0     3
   Inf   Inf   Inf   Inf     9     6     3     0

l =

     0     2     1     7     3     6     9    12

z =

     1     1     1     6     2     5     4     5

其中，

%l表示最短距离的向量
%z表示最短路的父节点的向量

• V1到V8的最短路为：V1->V2->V5->V8
• 最短路的距离为12