Simulink查表法实现NTC温度计算模型

原创于 2023-10-31 17:18:09 发布 · 2k 阅读

CC 4.0 BY-SA版权

文章标签：

29 篇文章

订阅专栏

前言

在实际项目中需要对NTC对某些区域进行温度采样和做一些系统层面的保护等等，比如过温降载，过温保护，这时就需要对NTC或者其他的温度传感器进行采样，计算实时温度。而NTC的数据表提供的温度和阻值的对应关系点数太少，计算的温度误差比较大。这里记录下所使用的方法，方便日后回顾。

如下图是开发板上的一个NTC电路。MCU采样NTC_Temp的AD值并进行温度的计算

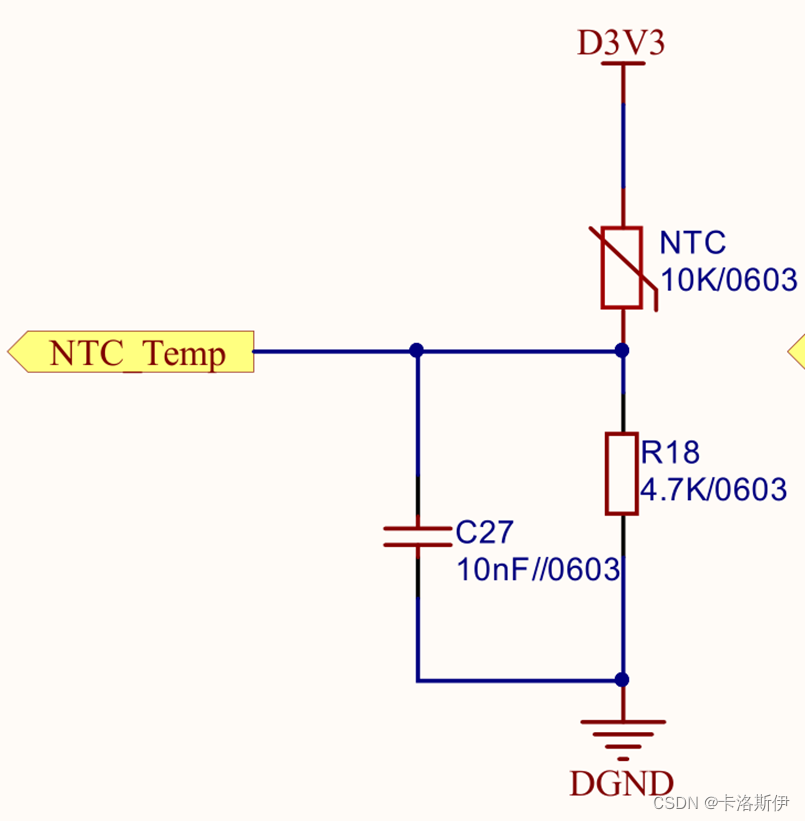
以下是NTC的阻值和温度的对应关系，这里选用的是10KR的型号

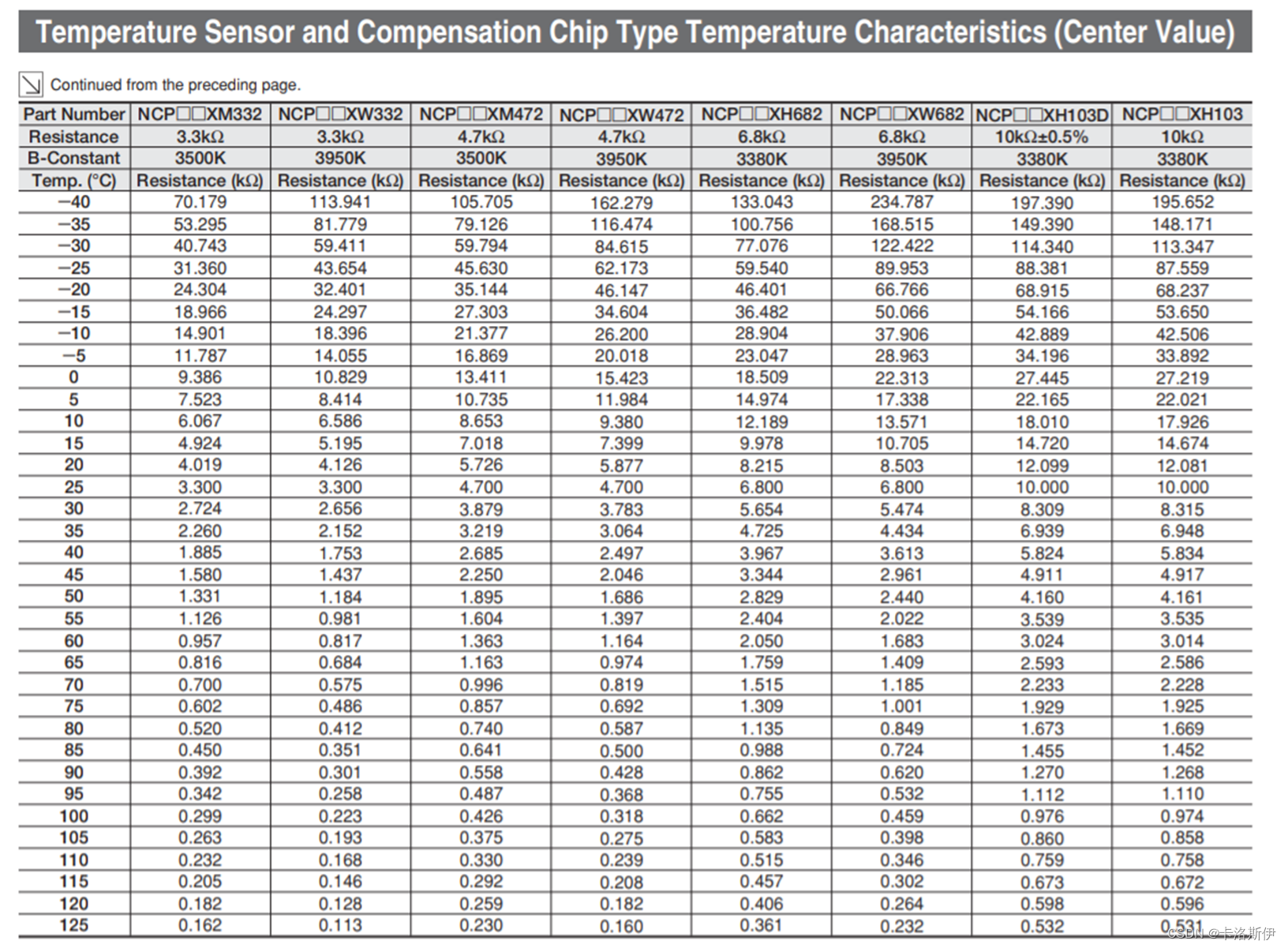
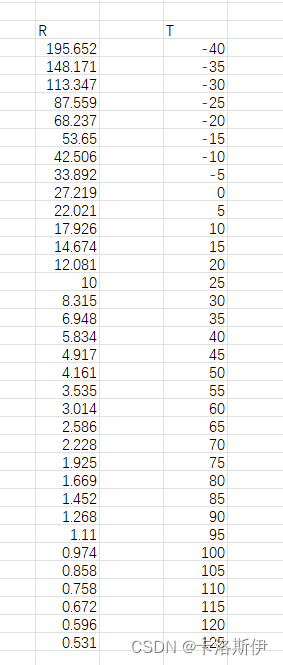
把数据手册上的数据导入到excel，如下是电阻和温度的对应关系，再根据电路结构很容易就算出了电压，AD值的对应关系。

如下是引脚电压和ADC对应当前的温度数据，再把数据生成曲线

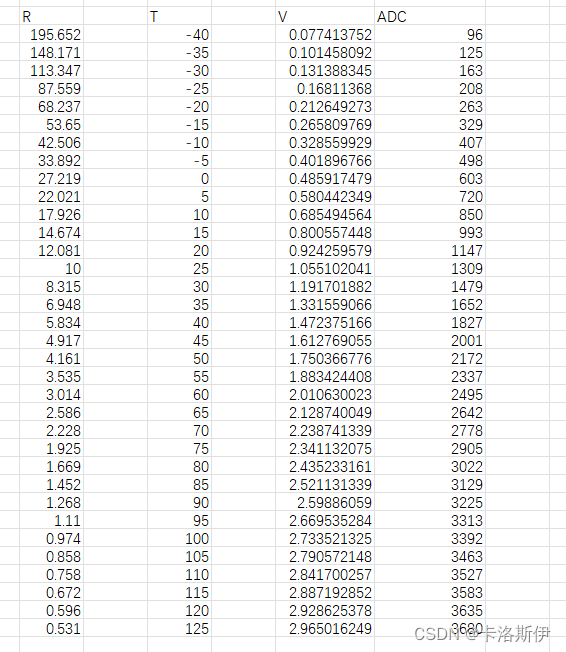
图1横坐标是AD值12位，纵坐标是对应的温度，图2是横坐标是电阻值，纵坐标是温度

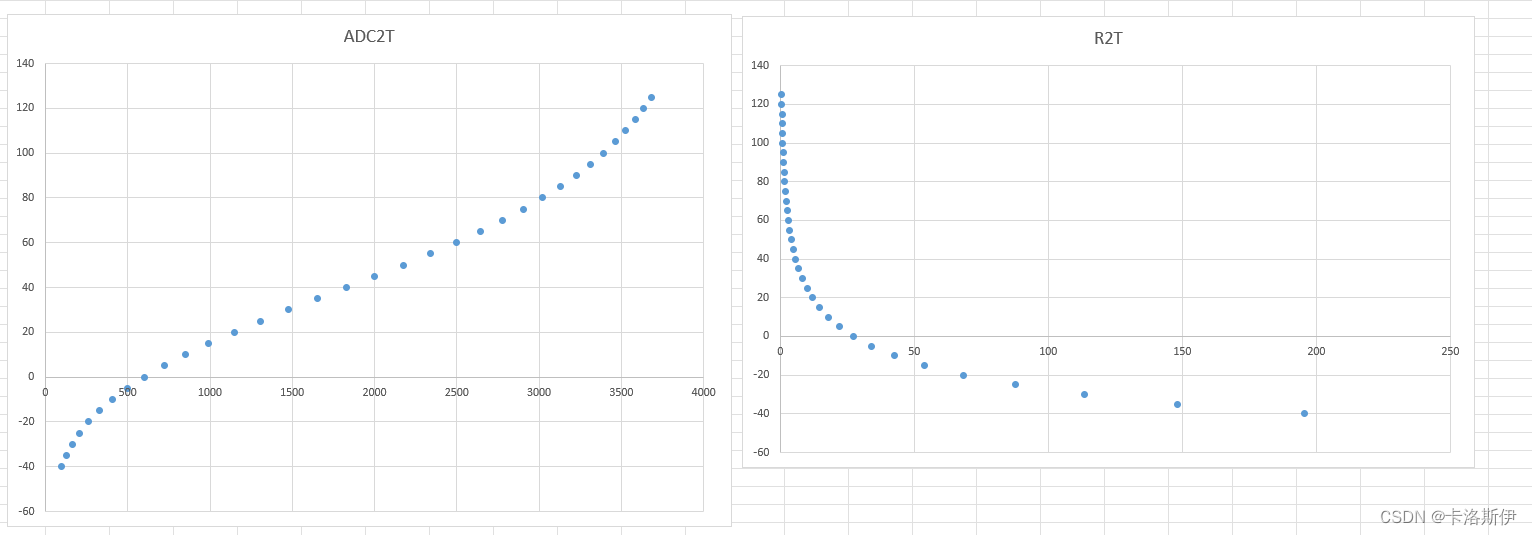
可以看到，曲线的点是比较少的，如果直接用这些数据进行查表，那得到的温度值精度也不高。

从Matlab里双击打开刚刚的表格，把表格数据导入到Workspace,如下

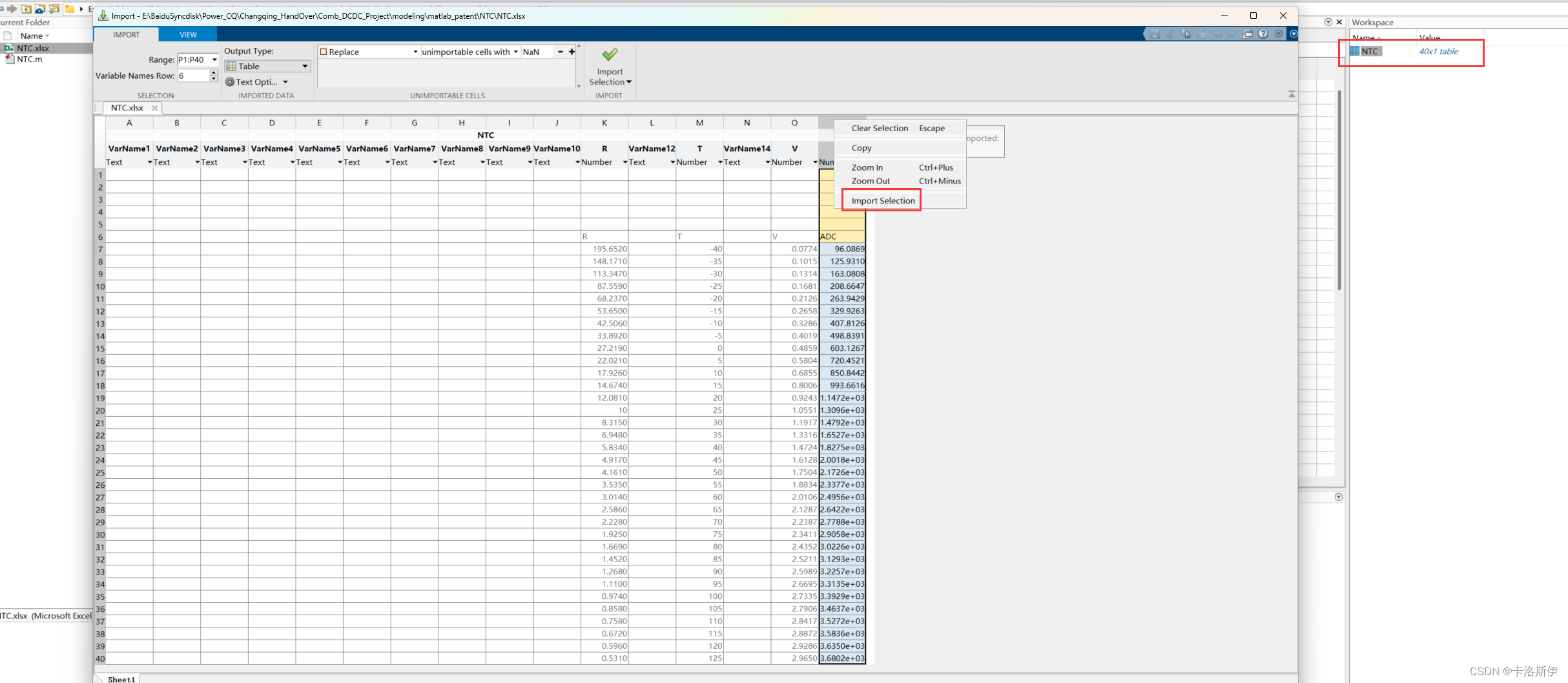
再把导入到Workspace里的数据给到两个数组，求个转转置就可以把列变成行了。

输入以下代码


Coef1=polyfit(ADC_Table_T,Tem_Table_T,5);
z1=polyval(Coef1,ADC_Table_T);
plot(ADC_Table_T,Tem_Table_T,'r*',ADC_Table_T,z1,'b')

第一句的意思是把ADC数组作为输入，把温度作为输出，拟合成一个5次多项式的形式，并获取其系数。

第二句就是把ADC数组作为输入，用拟合得到的系数方程计算得到温度Z1

第三句就是比较拟合出来的曲线和数组曲线作对比

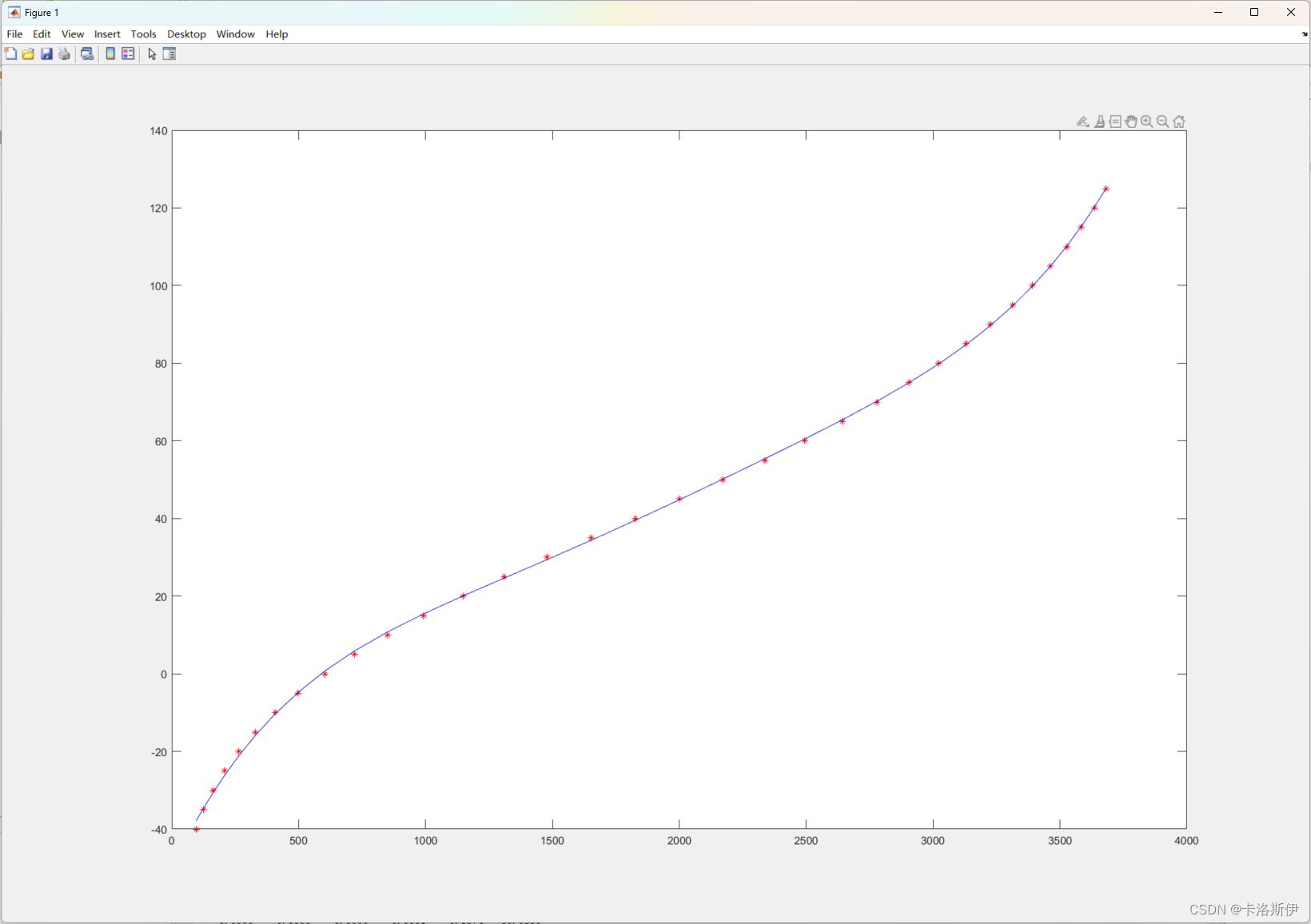
可以适当调节项数提高精度，如 Coef1=polyfit(ADC_Table_T,Tem_Table_T,5);这里采用的是五次项。

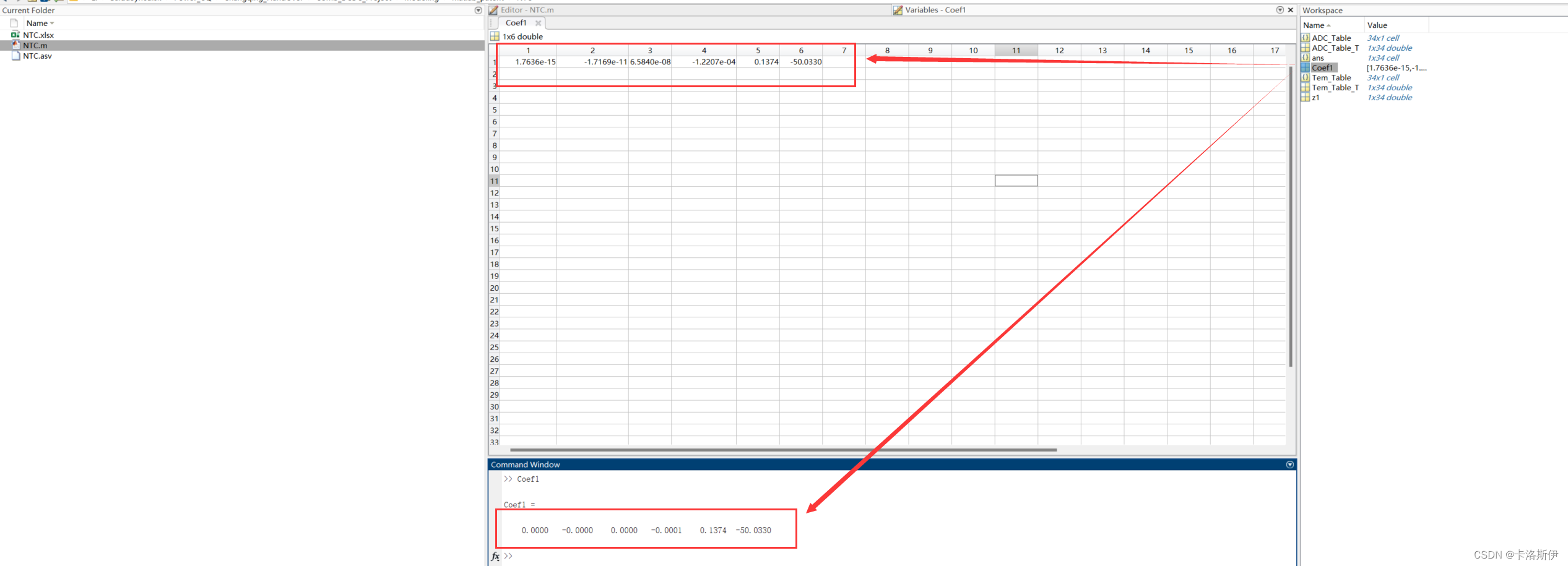
可以看到，系数在Command Window里面精度是不够的，需要在Workspace里双击。选择上面的系数，最后再把系数构建成多项式，那ADC和温度的关系就可以计算出来，后面根据需要的精度进行调整即可。

把计算公式输入到excel里，和之前的数据做对比，这里设置了从-40-125度一共191个点。可根据实际需要进行适当调整，精度越高占用空间越多，合理选择就可以。

再把数据导入到脚本里

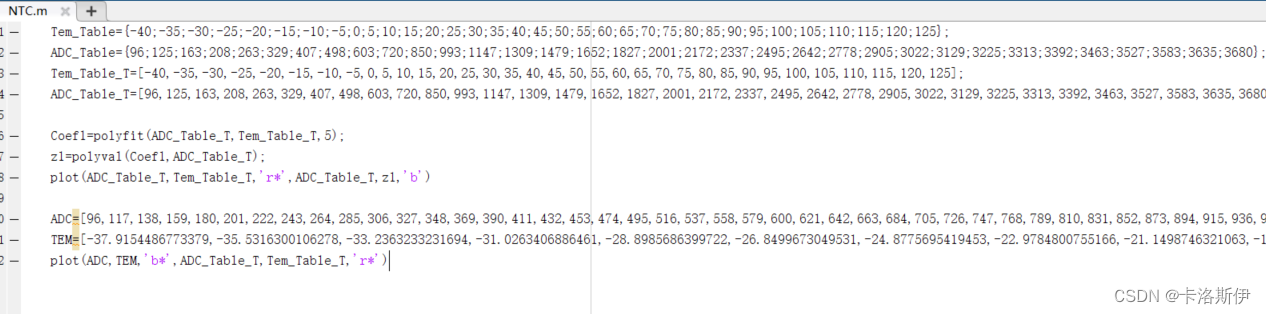
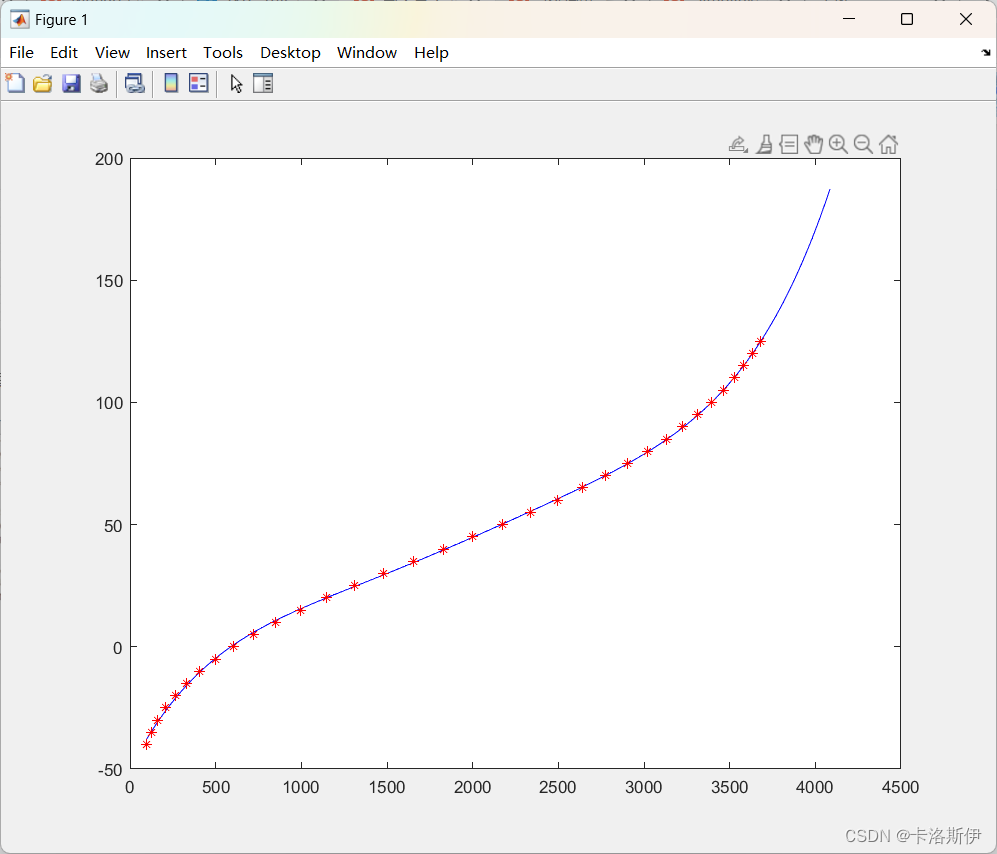
比较NTC数据手册提供的点，再比较拟合出来的191个点的曲线。

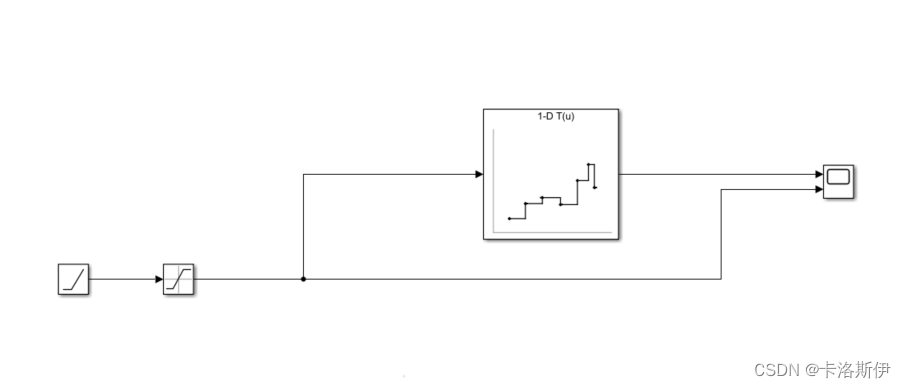
得到数据后直接用Simulink查表就可以完成ADC转换成温度值的计算了。

如下是模块内部配置

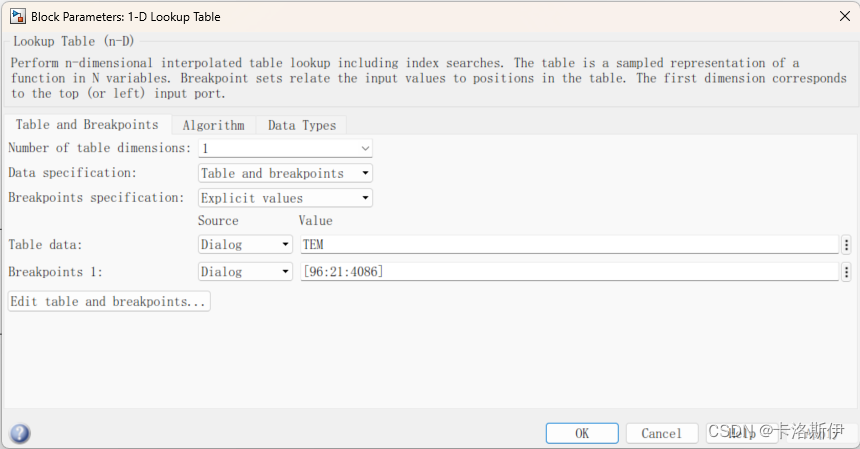
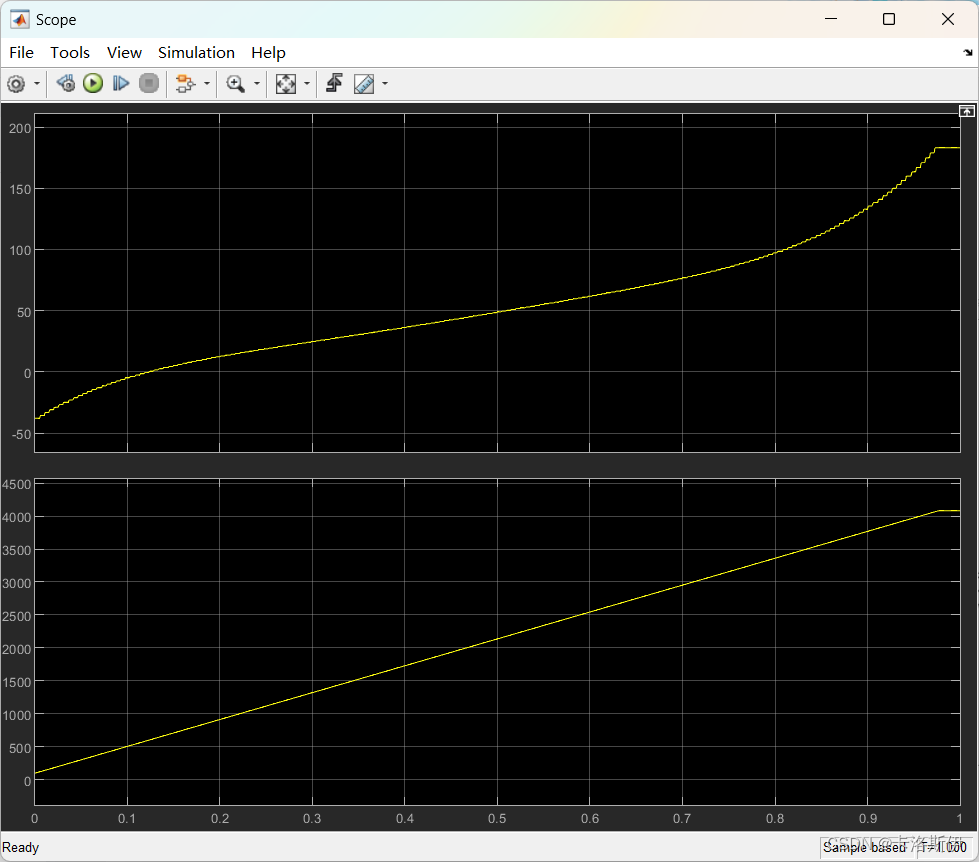
AD值改变，温度也会变化，仿真和预期一样，1-D LookupTable 这个模块可以直接生成代码。

没啥好总结的！灵活使用各种方法和工具就行，这种方法也可以用在其他复杂的公式里面，如一些曲线过于复杂不好拟合的，还可以分段拟合多项式等等，不同的情况选择合适的方法最重要。