可用矩阵运算实现图形绕点旋转

最新推荐文章于 2024-06-07 01:24:37 发布

油醋三椒

最新推荐文章于 2024-06-07 01:24:37 发布

阅读量1.1k

点赞数

分类专栏：数字多媒体技术文章标签：图形变化 python 绕点旋转

本文链接：https://blog.youkuaiyun.com/weixin_42664622/article/details/103673566

版权

数字多媒体技术专栏收录该内容

19 篇文章

订阅专栏

本文介绍如何使用矩阵运算实现坐标变换，包括图形绕特定点旋转的数学原理及其实现代码。此外，还详细解释了一种基于扫描线的多边形填充算法，通过创建并更新水平线段列表来填充多边形。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

介绍

可用矩阵运算实现坐标变换，当一个一个图形绕（ $x_f$ , $y_f$ ），旋转 $\theta$ 度的变化矩阵为
在这里插入图片描述
变化后的矩阵为
$\left[ \begin{matrix} x_1& y_1& 1\\ \end{matrix} \right] \ =\left[ \begin{matrix} x& y& 1\\ \end{matrix} \right] \times T_{rf}$

代码：

import numpy as np
from PIL import Image
from PIL import ImageDraw
from PIL import ImageFont
import math
 
array = np.ndarray((660, 660, 3), np.uint8)
array[:, :, 0] = 255
array[:, :, 1] = 112
array[:, :, 2] = 200
 
for i in range(0,660,1):
  array[i,330]=(0,0,0)
for j in range(0,660,1):
  array[330,j]=(0,0,0)
 
    
def creat_Net(point, row, y_min,y_max ): 
  # lists = [[] for i in range(3)]
  Net =  [([ ] * y_max ) for i in range(y_max )]
  # Net[0][0] = 0 
  print("row: ", y_max)
  # print("Net: ",Net) 
  point_count = point.shape[0]
  for j in range(0,  point_count):  
    x = np.zeros(10) 
    first = int(min(point[(j+1)%point_count][1] , point[j][1]))
    print("first: ",first)
    x[1] =  1/((point[(j+1)%point_count][1]-point[j][1])/(point[(j+1)%point_count][0]-point[j][0]))
    x[2] = max(point[(j+1)%point_count][1] , point[j][1])
    if(point[(j+1)%point_count][1] < point[j][1]):
      x[0] = point[(j+1)%point_count][0]  
    else:
      x[0] = point[j][0]
    Net[first].append(x)
  return Net

def draw_line(i,x ,y ): 
  array[330-i,int(x)+330] = (0,0,255) 
  rorate(  i , int(x)  )
  array[330-i,int(y) +330] = (0,0,255) 
  rorate(  i ,int(y)  )

def rorate( x ,y ): 
  t  = [ x, y, 1 ]
  t1 = [[1, 0, -10], [0, 1, 10], [ 0, 0, 1]]
  t2 = [[1, 0, 10], [0, 1, -10], [0, 0, 1]]
  r  = [[math.cos(math.radians(45)), -math.sin(math.radians(45)), 0], \
    [math.sin(math.radians(45)), math.cos(math.radians(45)), 0], [0, 0, 1]]
  re = np.dot(t ,t1)
  re = np.dot(re, r)
  re = np.dot(re, t2)
  print(re[0],re[1])
  array[330- int(re[0]),int(re[1])+330   ] = (0,0,255)
  

def polygon_fill(point):
  y_min = np.min(point[:,1])
  y_max = np.max(point[:,1])
  Net = creat_Net(point, y_max - y_min + 1, y_min, y_max)
  x_sort = [] * 3
  for i in range(y_min, y_max):
    x = Net[i]
    if(len(x) != 0):
      for k in x :
        x_sort.append(k)
    x_image = [] * 3  
    for cell in x_sort:
      x_image.append(cell[0])
    x_image.sort()
    if(len(x_image) >= 3 and x_image[0]==x_image[1] and x_image[2]>x_image[1]):
      x_image[1] = x_image[2]
    # print("x_: ",x_image[0],"x_image[1]: ",x_image[1])
    draw_line(i, x_image[0], x_image[1]) 
    
    linshi = [] * 3
    for cell in x_sort:
      if cell[2] > i: 
        cell[0] += cell[1]
        linshi.append(cell)
    x_sort = linshi[:]

  x_image = [] * 3  
  for cell in x_sort:
    x_image.append(cell[0])
  x_image.sort()
  
  draw_line(i, x_image[0],x_image[1])


def main():
  point = [[55,40], [100,80], [100,160],[55,180], [10,160], [10,80]]
  point = np.array(point)
  polygon_fill( point )
  image = Image.fromarray(array)
  image.show() 

if __name__ == "__main__":
  main()

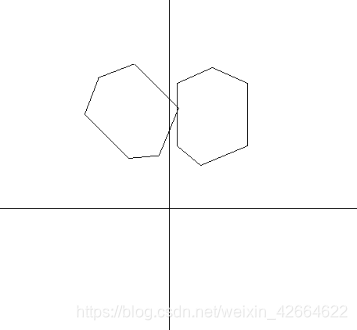
在这里插入图片描述