python照相机标定、在图像中放置虚拟物体、PyGame和PyOpenGL

一、照相机标定
标定照相机是指计算出该照相机的内参数，在我们的例子中，是指计算矩阵K，如果你的应用要求高精度，那么可以扩展照相机模型，使其包含径向畸变和其他条件。对于大多数应用来说，简单的照相机模型已经足够。标定照相机的标准方法是，拍摄多幅平面棋盘模式的图像，然后进行处理计算。
照相机的测量值写入辅助函数中，图像大小为：2592*1936像素：

def my_calibration(sz):
    row, col = sz
    fx = 2555*col/2592
    fy = 2586*row/1936
    K = diag([fx, fy, 1])
    K[0, 2] = 0.5*col
    K[1, 2] = 0.5*row
    return K

二、以平面和标记物进行姿态评估：
如果图像中包含平面状的标记物，并且已经对照相机进行了标定，那么我们可以计算出照相机的姿态，这里的标记物体可以为任何平坦的物体。下面我们借助图一和图二提取图像的sift特征，然后使用RANSAC算法稳健地估计单应性矩阵：


运行代码找出特征，并映射在另一张照片中：

sift.process_image('book_frontal.JPG', 'im0.sift')
l0, d0 = sift.read_features_from_file('im0.sift')

sift.process_image('book_perspective.bmp', 'im1.sift')
l1, d1 = sift.read_features_from_file('im1.sift')


# match features and estimate homography
matches = sift.match_twosided(d0, d1)
ndx = matches.nonzero()[0]
fp = homography.make_homog(l0[ndx, :2].T)
ndx2 = [int(matches[i]) for i in ndx]
tp = homography.make_homog(l1[ndx2, :2].T)

model = homography.RansacModel()
H, inliers = homography.H_from_ransac(fp, tp, model)

运行结果为：


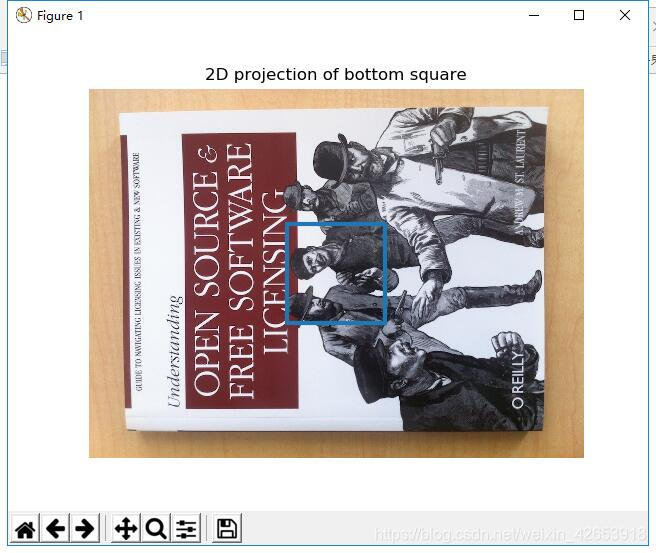
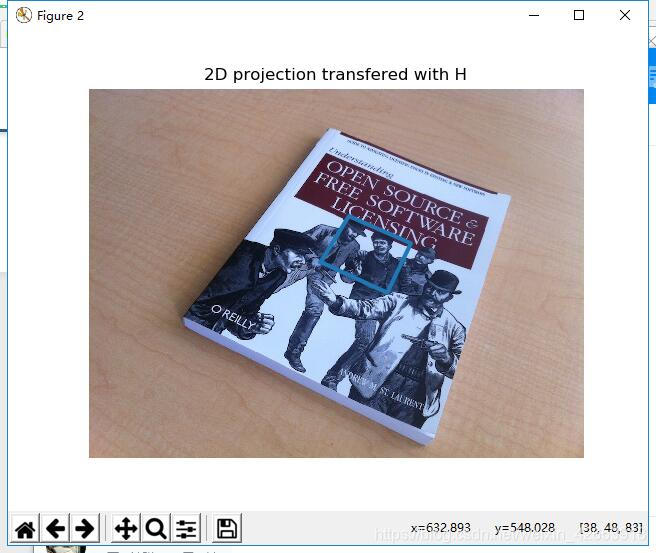
下面我们定义相应的三维坐标系，使其标定物体在X-Y平面上，原点在标记物的某位置上。可以使用下面的函数来产生立方体的点：

def cube_points(c, wid):  # 绘制立方体的一各点列表
    """ Creates a list of points for plotting
        a cube with plot. (the first 5 points are
        the bottom square, some sides repeated). """
    p = []
    # 底部
    p.