遗传算法

1.基本思想

遗传算法的基本思想是从初始种群出发，采用优胜劣汰，适者生存的自然法则选择个体，并通过杂交，变异来产生新一代种群，如此逐代进化，直到满足目标为止。

2.算法流程

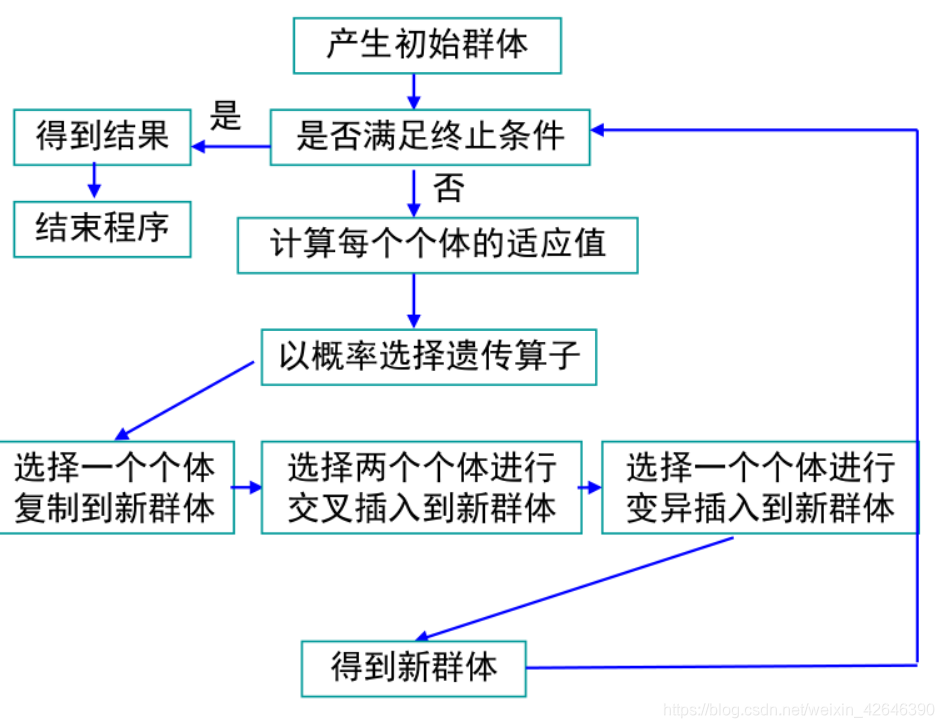
3.算法实现

3.1 GA算法实现

clc;clear all;

format long;%设定数据显示格式

%初始化参数

T=500;%仿真代数

N=50;% 群体规模

pm=0.05;pc=0.8;%交叉变异概率

umax=30;umin=-30;%参数取值范围

L=10;%单个参数字串长度，总编码长度Dim*L
Dim=2;%Dim维空间搜索

bval=round(rand(N,Dim*L));%初始种群，round函数为四舍五入

bestv=-inf;%最优适应度初值
funlabel=2;       %选择待优化的函数，1为Rastrigin,2为Schaffer,3为Griewank，4为Sphere
Drawfunc(funlabel);%画出待优化的函数，只画出二维情况作为可视化输出

%迭代开始

for ii=1:T

%解码，计算适应度

    for i=1:N  %对每一代的第i个粒子
        for k=1:Dim
            y(k)=0;
            for j=1:1:L  %从1到L，每次加以1

               y(k)=y(k)+bval(i,k*L-j+1)*2^(j-1);%把第i个粒子转化为十进制的值，例如y1是第一维

            end 
            x(k)=(umax-umin)*y(k)/(2^L-1)+umin;%转化为实际的x1
        end

  %     obj(i)=100*(x1*x1-x2).^2+(1-x1).^2; %目标函数 
       obj(i)=fun(x,funlabel);
       xx(i,:)=x;

    end

    func=obj;%目标函数转换为适应度函数

    p=func./sum(func);

    q=cumsum(p);%累加

    [fmax,indmax]=max(func);%求当代最佳个体

   if fmax>=bestv

      bestv=fmax;%到目前为止最优适应度值

      bvalxx=bval(indmax,:);%到目前为止最佳位串

      optxx=xx(indmax,:);%到目前为止最优参数

   end   

   Bfit1(ii)=bestv; % 存储每代的最优适应度

%%%%遗传操作开始

%轮盘赌选择

 for i=1:(N-1)

    r=rand;

    tmp=find(r<=q);

    newbval(i,:)=bval(tmp(1),:);

 end

  newbval(N,:)=bvalxx;%最优保留

  bval=newbval;

%单点交叉

    for i=1:2:(N-1)

       cc=rand;

       if cc<pc

           point=ceil(rand*(2*L-1));%取得一个1到2L-1的整数

           ch=bval(i,:);

           bval(i,point+1:2*L)=bval(i+1,point+1:2*L);

           bval(i+1,point+1:2*L)=ch(1,point+1:2*L);

        end

    end   

    bval(N,:)=bvalxx;%最优保留

    %位点变异

    mm=rand(N,Dim*L)<pm;%N行

    mm(N,:)=zeros(1,Dim*L);%最后一行是精英不变异，强制赋0

    bval(mm)=1-bval(mm); 

end

%输出
figure;

plot(-Bfit1);% 绘制最优适应度进化曲线

bestv   %输出最优适应度值

optxx    %输出最优参数

3.2 画图代码实现

function Drawfunc(label)

x=-5:0.05:5;%41列的向量
if label==1
    y = x;
    [X,Y] = meshgrid(x,y);
    [row,col] = size(X);
    for  l = 1 :col
         for  h = 1 :row
            z(h,l) = Rastrigin([X(h,l),Y(h,l)]);
        end
    end
    surf(X,Y,z);
    shading interp
    xlabel('x1-axis'),ylabel('x2-axis'),zlabel('f-axis'); 
    title('mesh'); 
end

if label==2
    y = x;
    [X,Y] = meshgrid(x,y);
    [row,col] = size(X);
    for  l = 1 :col
         for  h = 1 :row
            z(h,l) = Schaffer([X(h,l),Y(h,l)]);
        end
    end
    surf(X,Y,z);
    shading interp 
    xlabel('x1-axis'),ylabel('x2-axis'),zlabel('f-axis'); 
    title('mesh'); 
end

if label==3
    y = x;
    [X,Y] = meshgrid(x,y);
    [row,col] = size(X);
    for  l = 1 :col
         for  h = 1 :row
            z(h,l) = Griewank([X(h,l),Y(h,l)]);
        end
    end
    surf(X,Y,z);
    shading interp 
    xlabel('x1-axis'),ylabel('x2-axis'),zlabel('f-axis'); 
    title('mesh'); 
end
if label==4
    y = x;
    [X,Y] = meshgrid(x,y);
    [row,col] = size(X);
    for  l = 1 :col
         for  h = 1 :row
            z(h,l) =Sphere([X(h,l),Y(h,l)]);
        end
    end
    surf(X,Y,z);
    shading interp 
    xlabel('x1-axis'),ylabel('x2-axis'),zlabel('f-axis'); 
    title('mesh'); 
end



    

3.3 目标函数为Griewank

Griewank数学公式为：

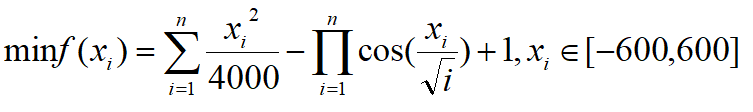
代码实现：

function y=Griewank(x)
%Griewan函数
%输入x,给出相应的y值,在x=(0,0,…,0)处有全局极小点0.
%编制人：
%编制日期：
[row,col]=size(x);
if row>1
    error('输入的参数错误');
end
y1=1/4000*sum(x.^2);
y2=1;
for h=1:col
    y2=y2*cos(x(h)/sqrt(h));
end
y=y1-y2+1;
%y=-y;

3.1.1解空间维度恒定不变为2，改变种群数量。
当种群数量为10，运行结果如下：

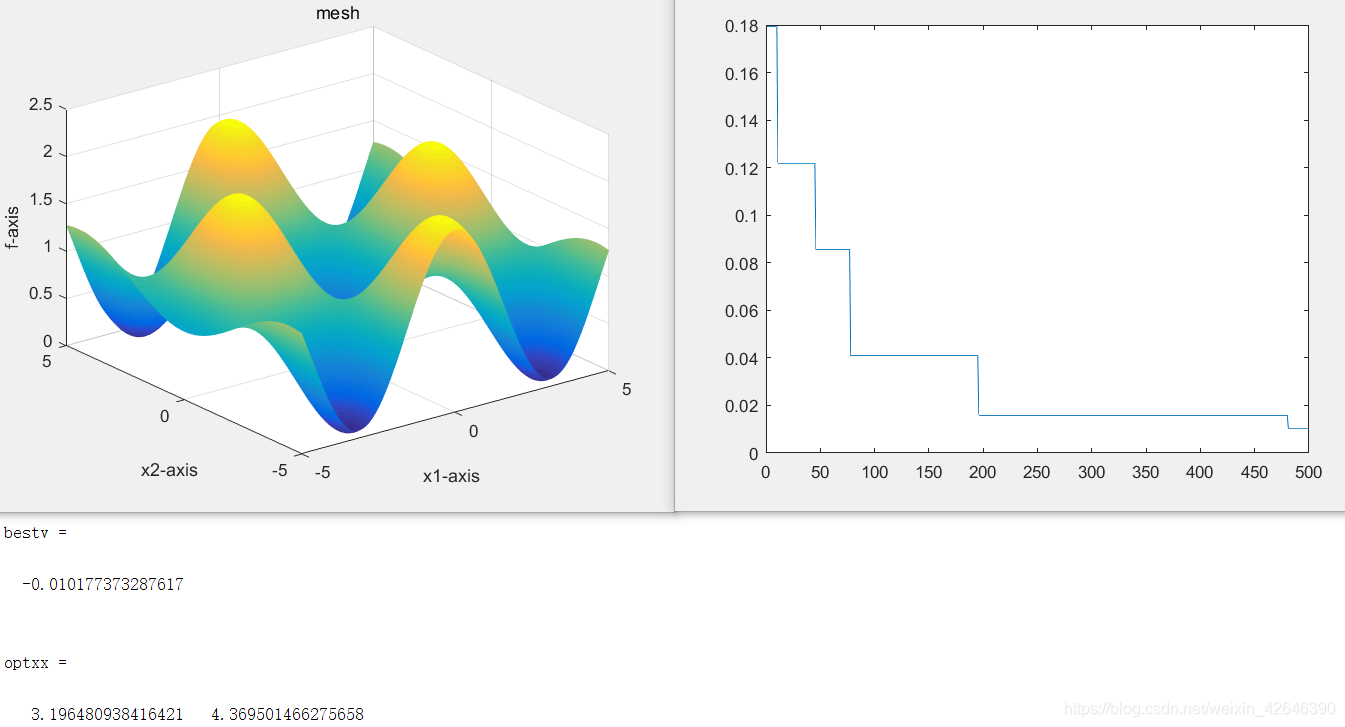
当种群数量为20，运行结果如下：

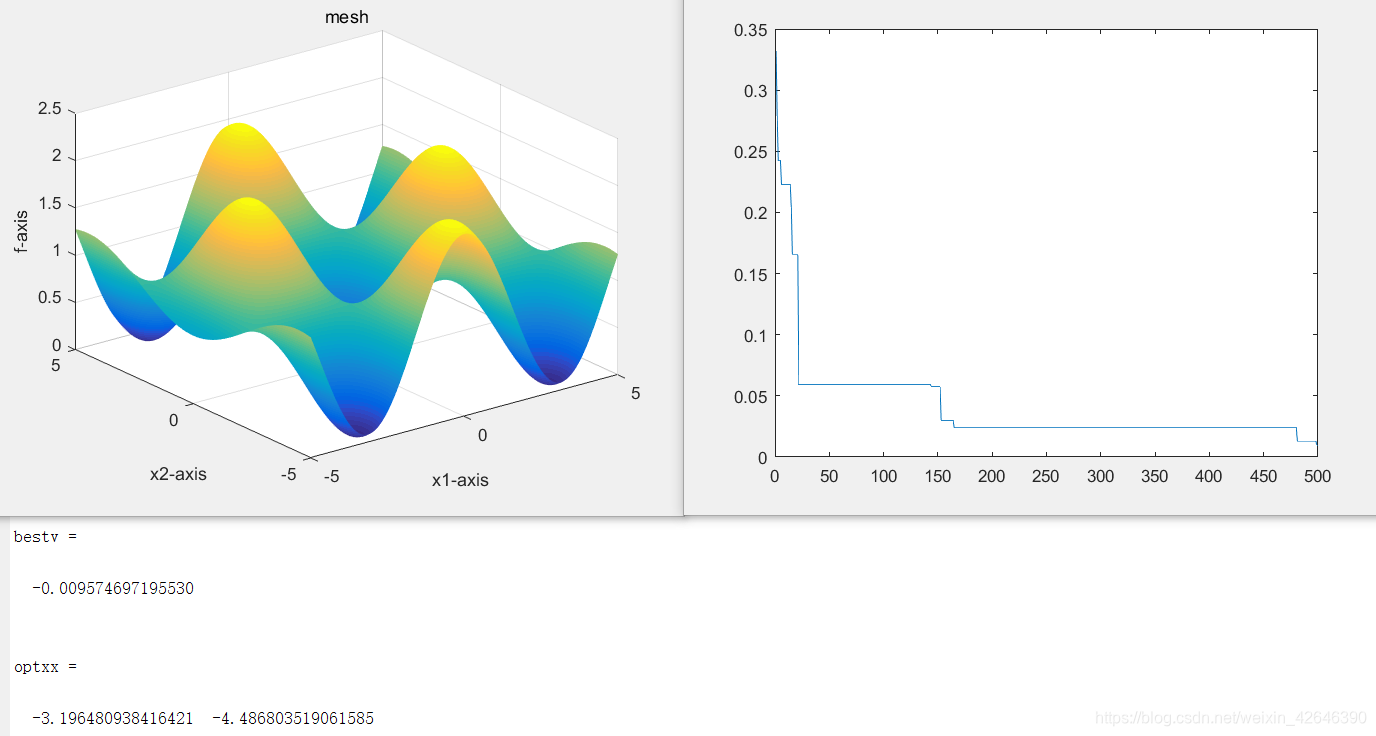
当种群数量为40，运行结果如下：

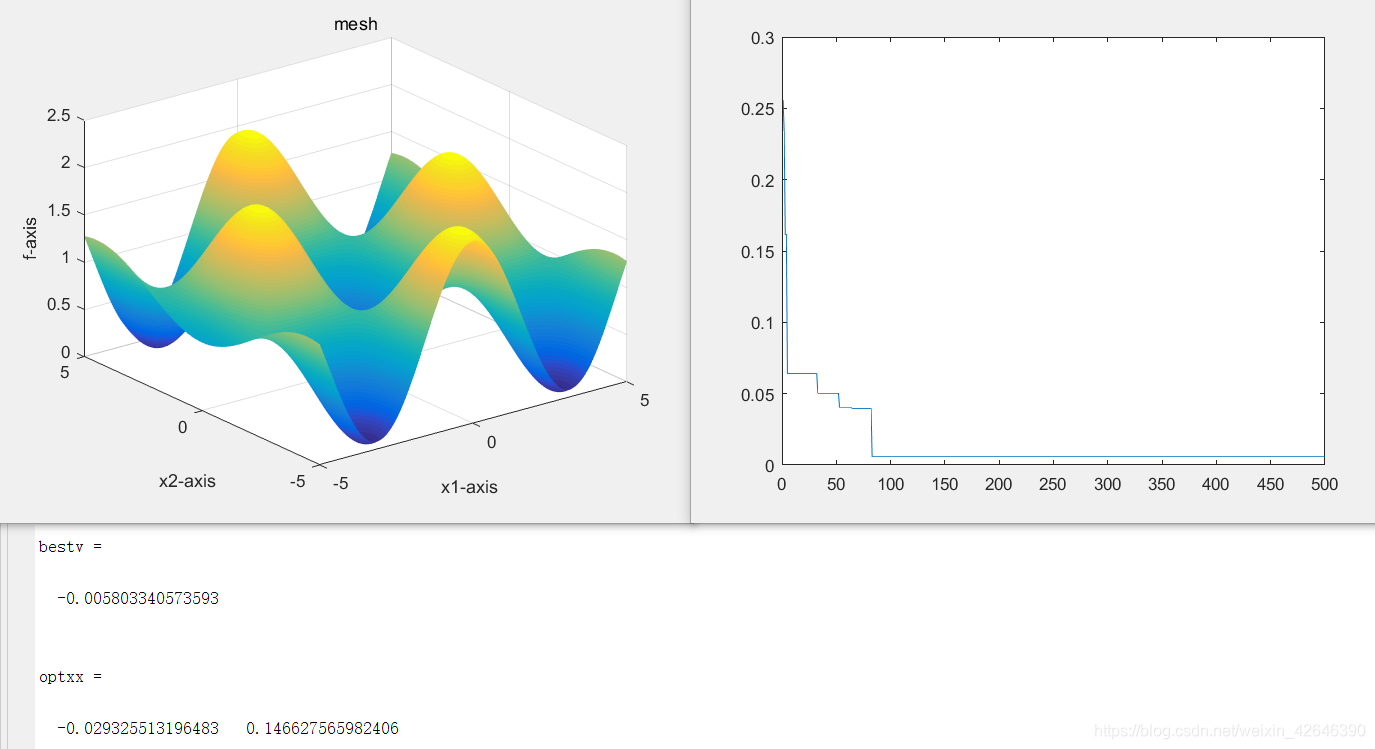
当种群数量为60时，运行结果如下：

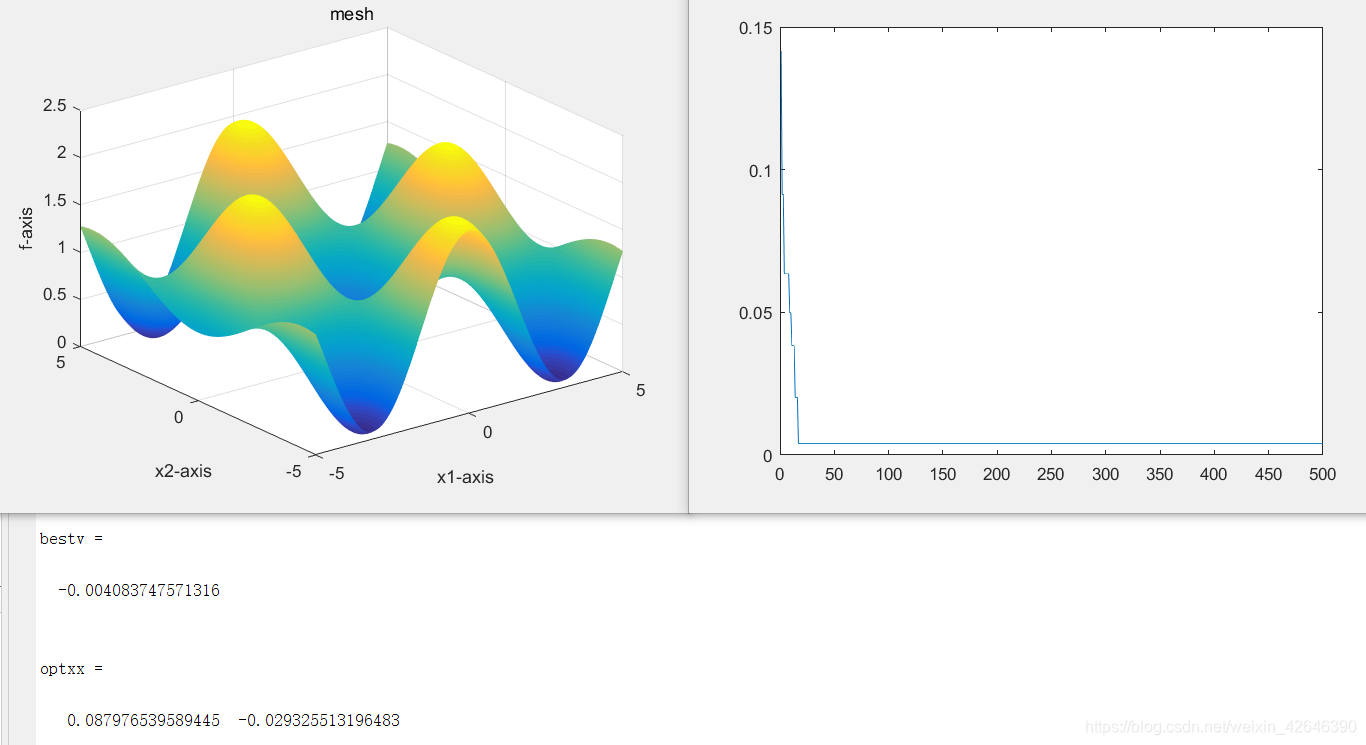
结果分析：当解空间维度不变时，随着种群数量的增大，最优适应度的值逐渐增大，最优适应度曲线达到平衡的迭代次数减少，曲线波动较大。

3.1.2 种群数量恒定为40，改变解空间维度
当解空间维度为5时，运行结果如下：

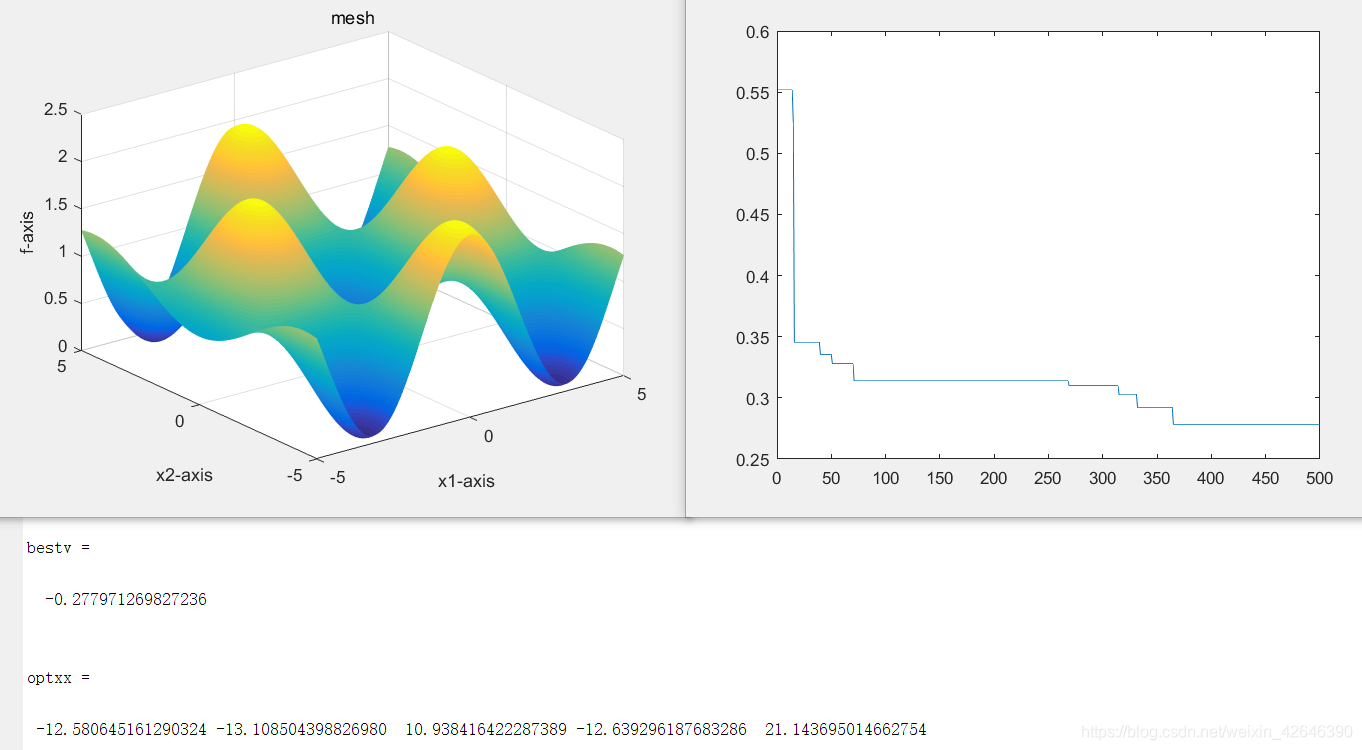
当解空间为10时，运行结果如下：

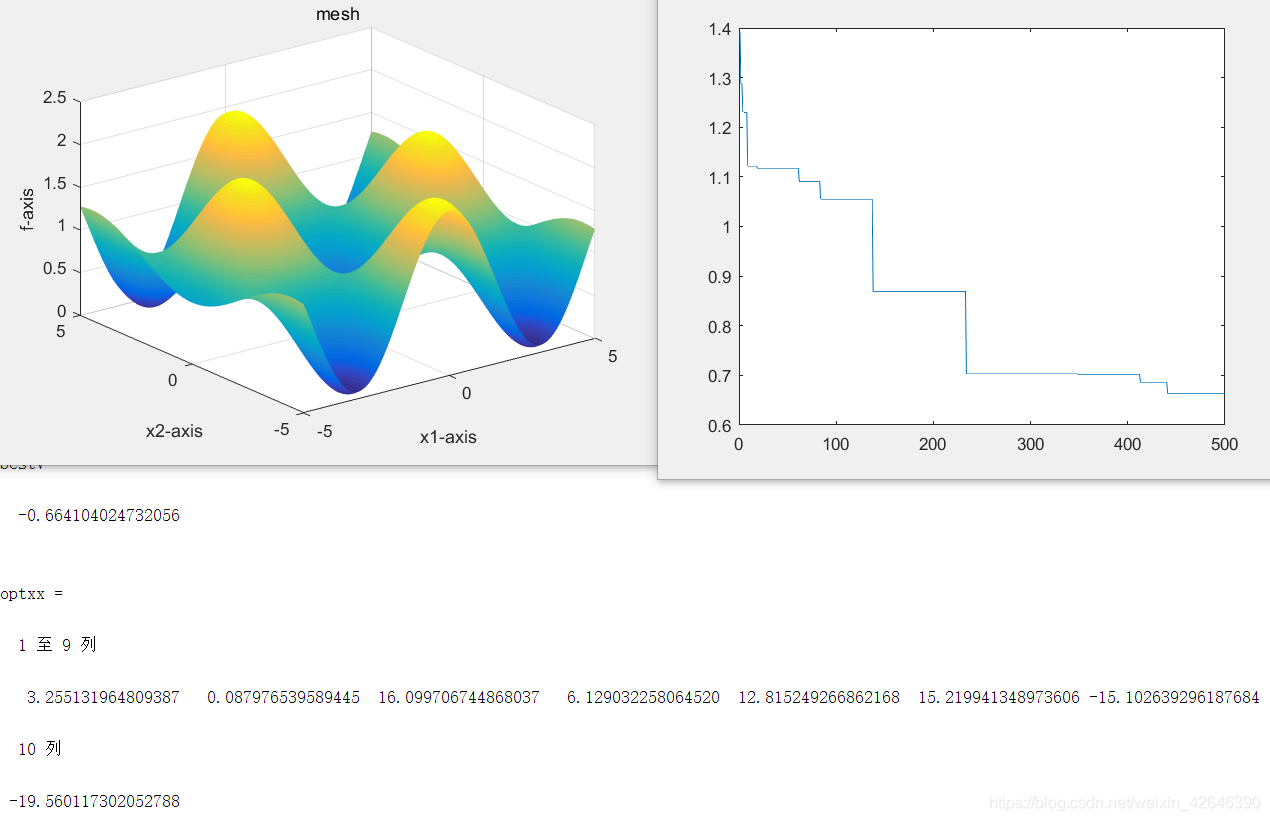
当空间维度为20时，运行结果如下：

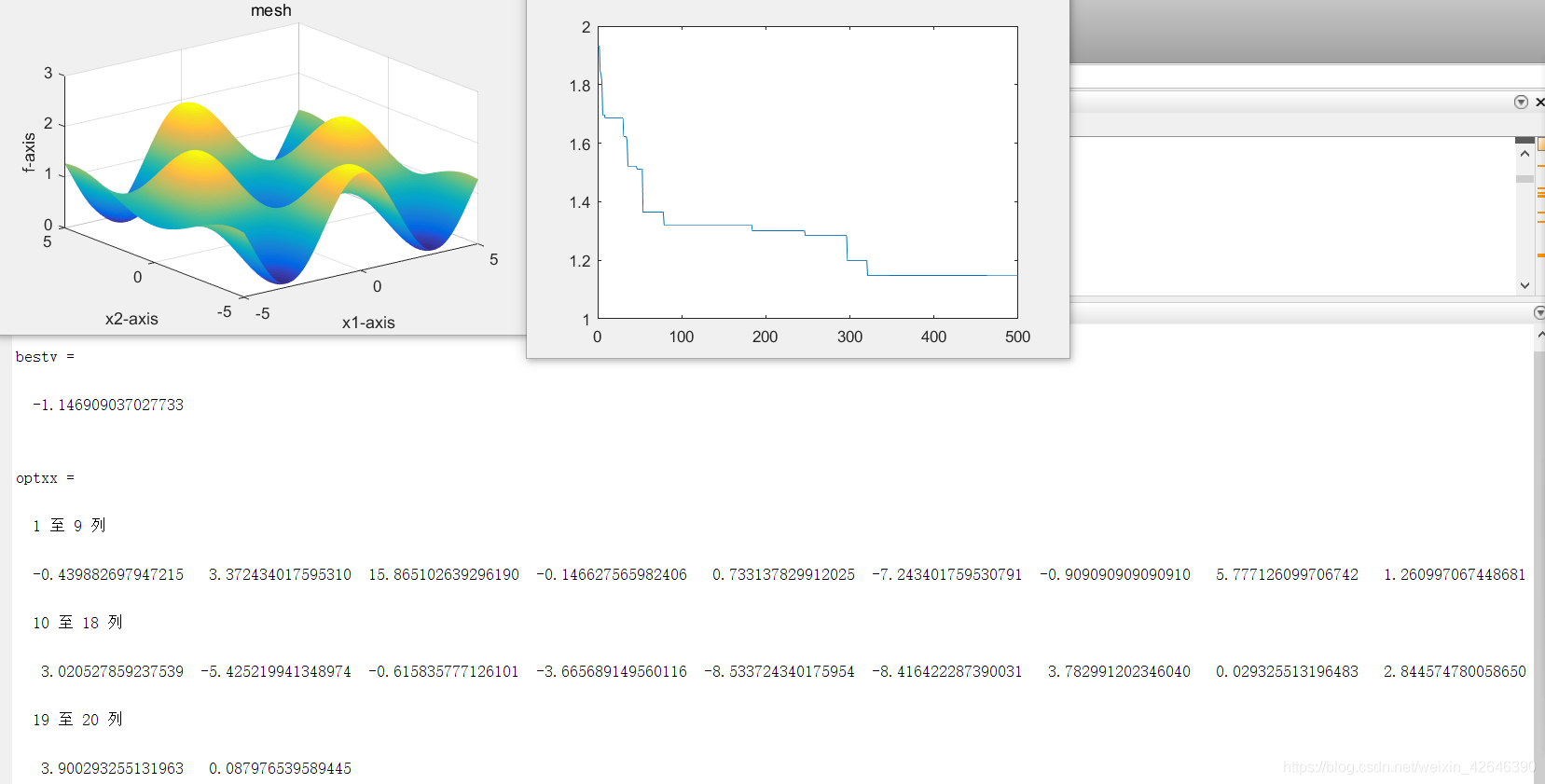
结果分析：当种群数量不变时，随着解空间维度的增大，最优适应度逐渐增大。

3.2 目标函数为Rastrigin

数学公式为

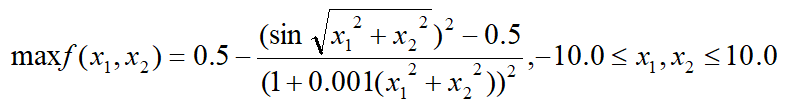
代码实现：

function y = Rastrigin(x)
% Rastrigin函数
% 输入x,给出相应的y值,在x = ( 0 , 0 ,…, 0 )处有全局极小点0.
% 编制人：
% 编制日期：
[row,col] = size(x);
if  row > 1 
    error( ' 输入的参数错误 ' );
end
y =sum(x.^2-10*cos(2*pi*x)+10);
%y =-y;

3.2.1 解空间维度恒定不变为2，改变种群数量。
种群数量为20时，结果如下：

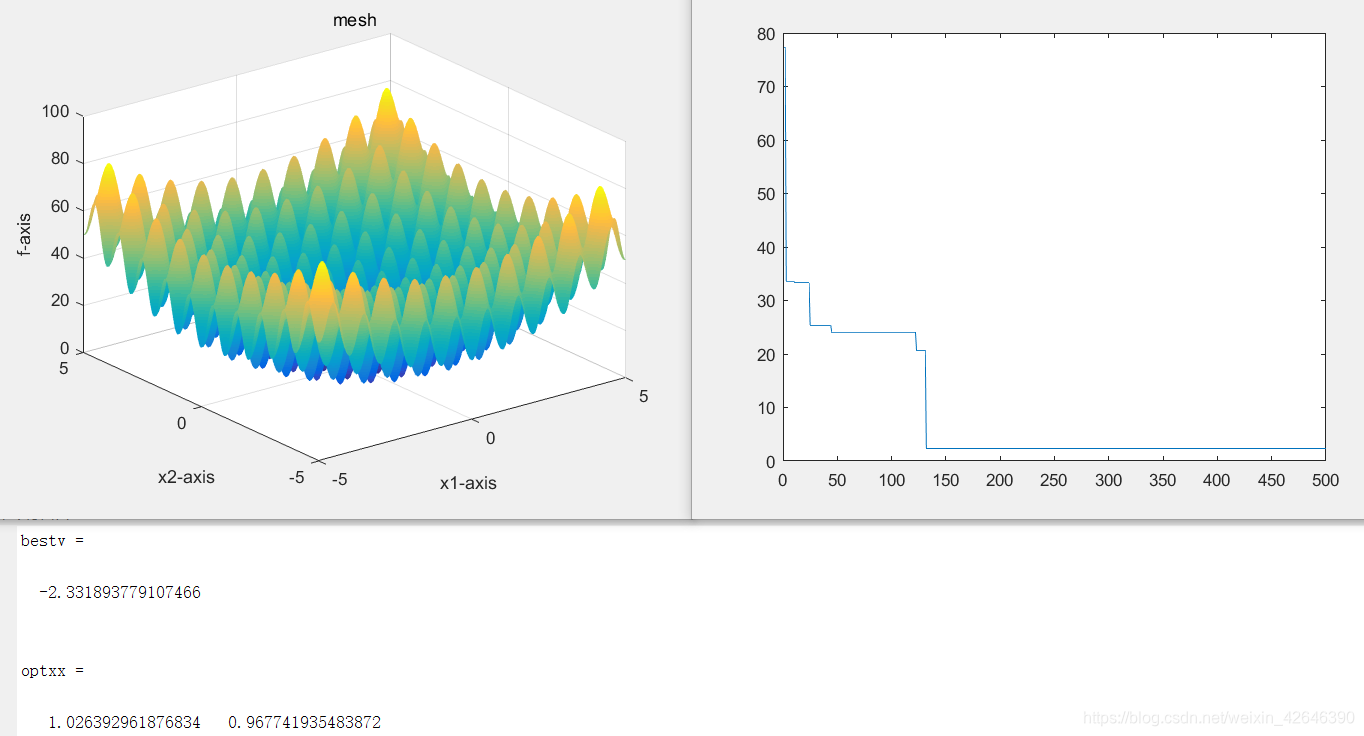
种群数量为40时，结果如下：

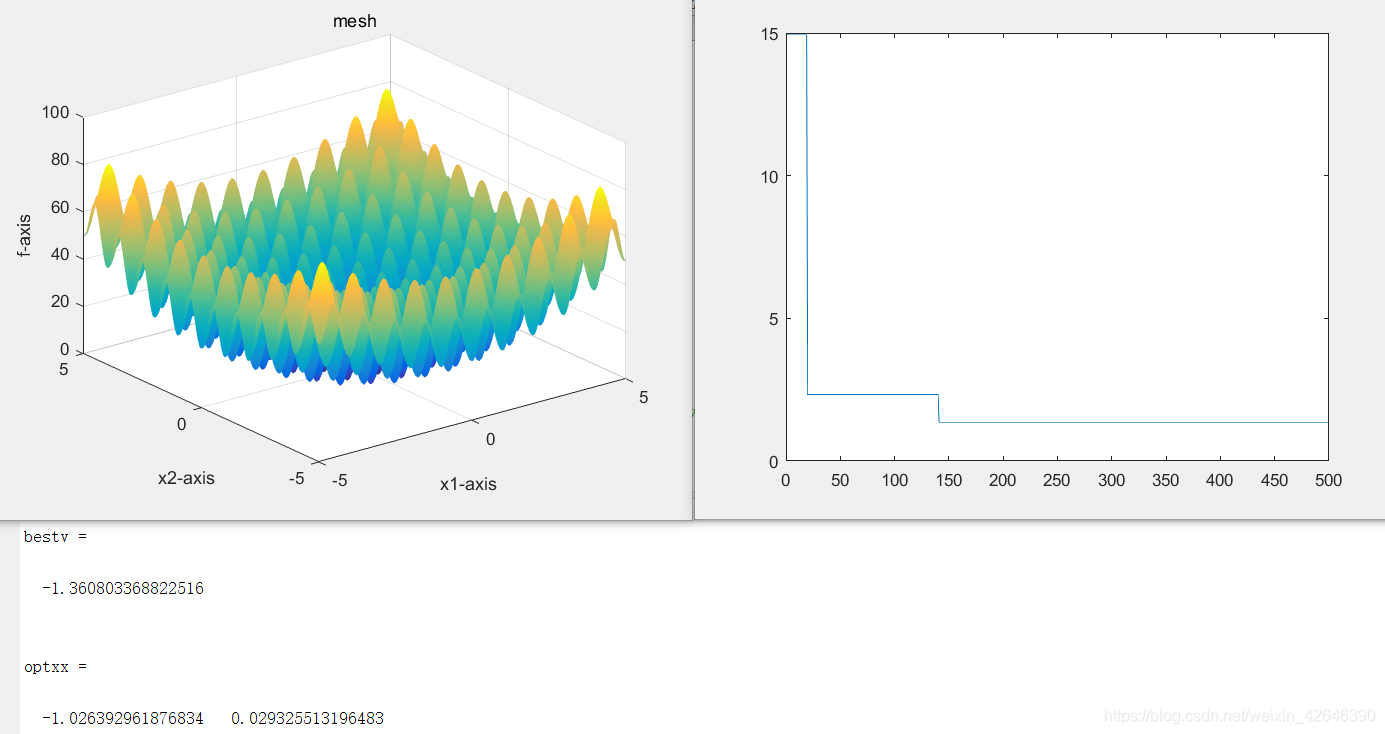
种群数量为80时，结果如下：

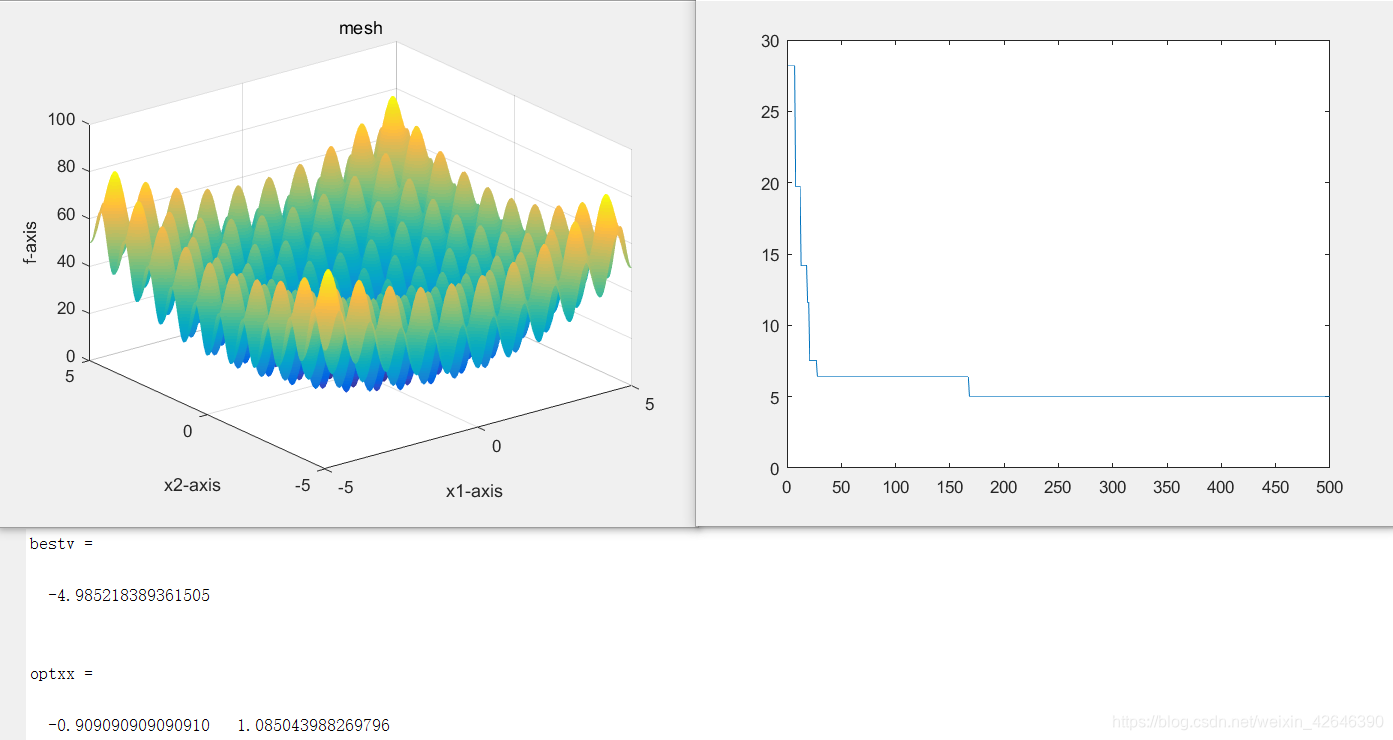
结果分析：当解空间维度不变时，随着种群数量的增大，最优适应度曲线趋于平稳的迭代次数增大。最优适应度是先增大后减小。
3.2.2种群数量恒定为20，改变解空间维度
当解空间维度为5时，结果如下：

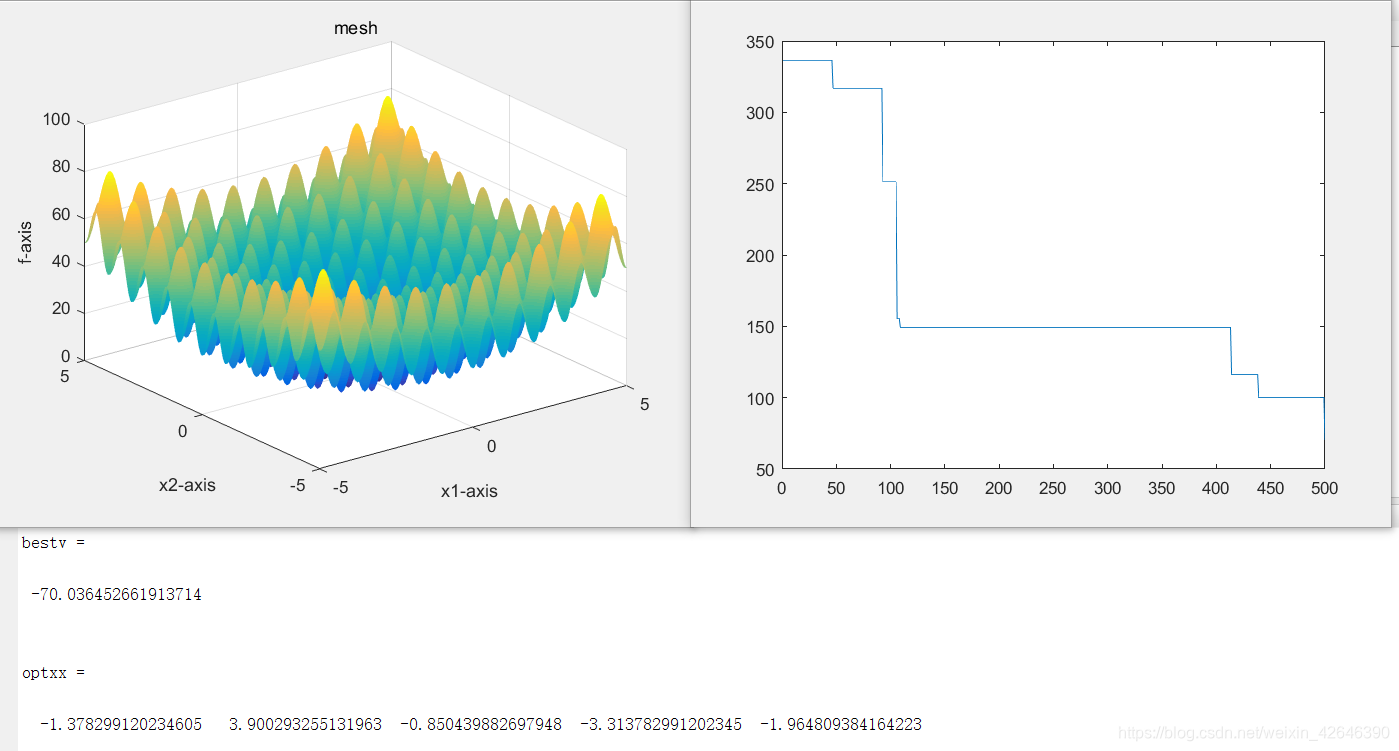
当解空间维度为10时，结果如下：

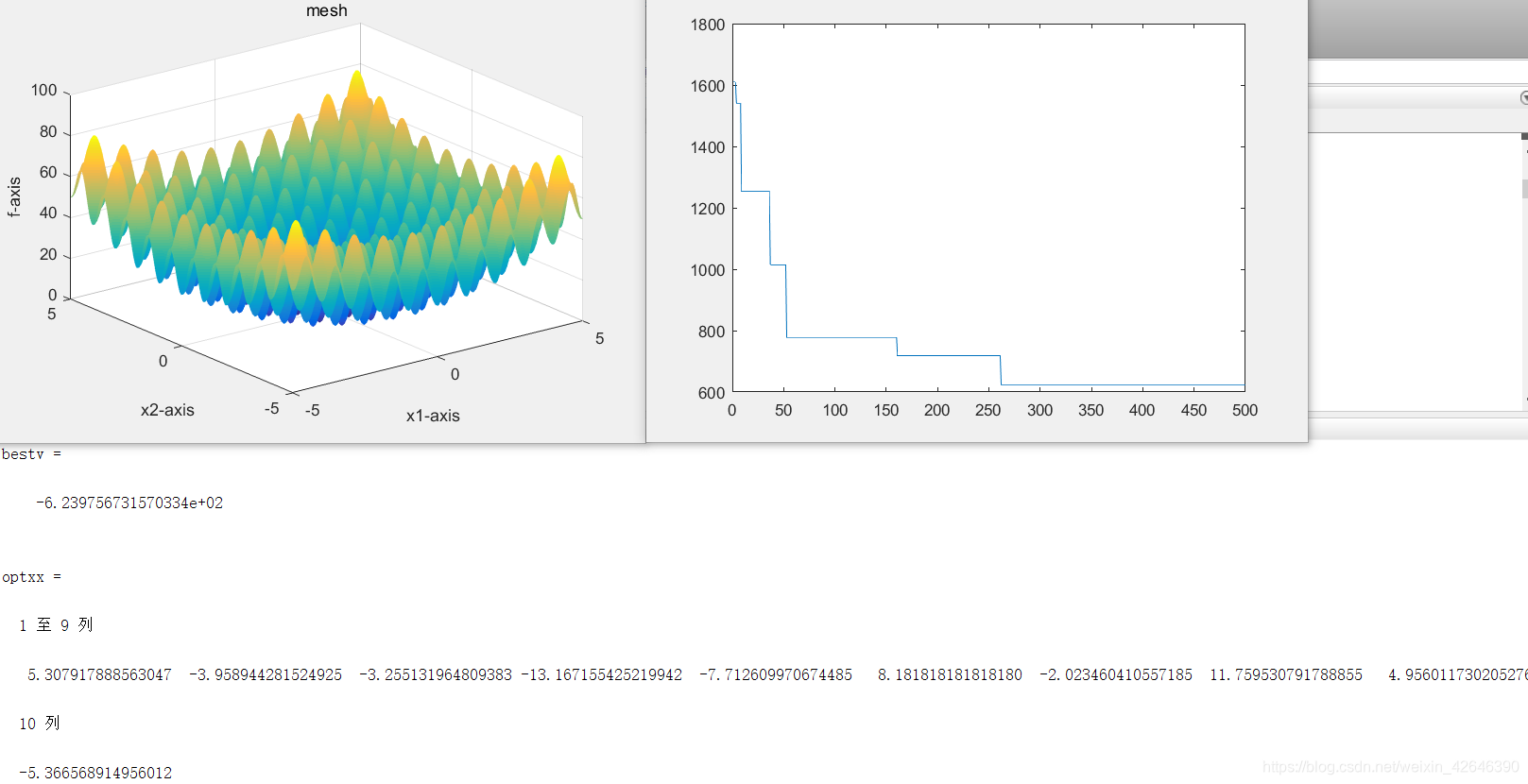
当解空间维度为15时，结果如下：

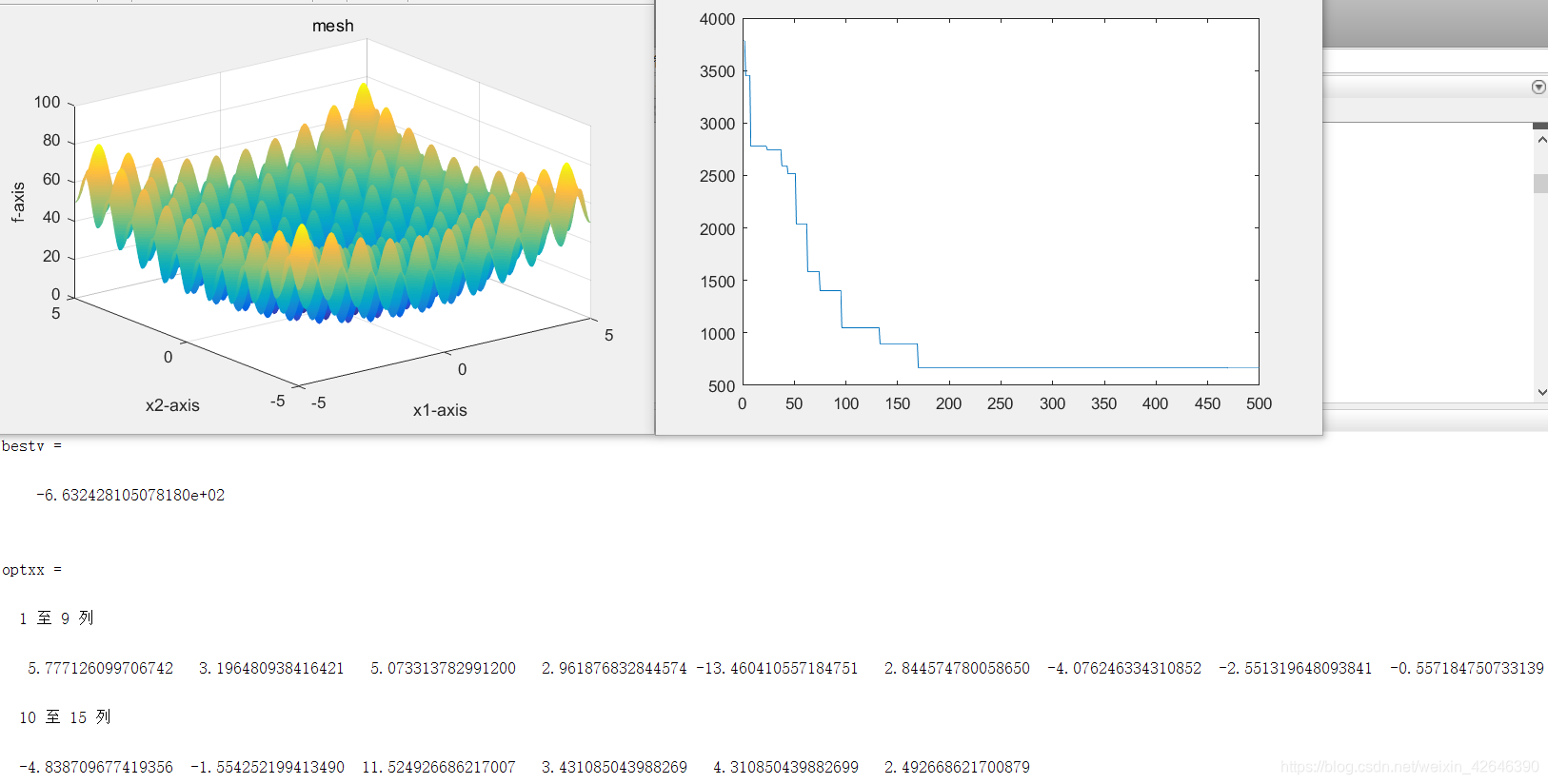
结果分析：当种群数量不变时，随着解空间维度的增大，最优适应度曲线到达平稳的迭代次数逐渐减少，最优适应度逐渐增大。
3.3 目标函数为Sphere
数学公式为：

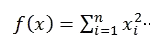
代码实现：

function y=Sphere(x)
[row,col]=size(x);
if row>1
    error('输入的参数错误');
end
y=30*sum(x.^2);
y=-y;

3.3.1 解空间维度不变，改变种群数量
当种群数量为20时，结果如下：

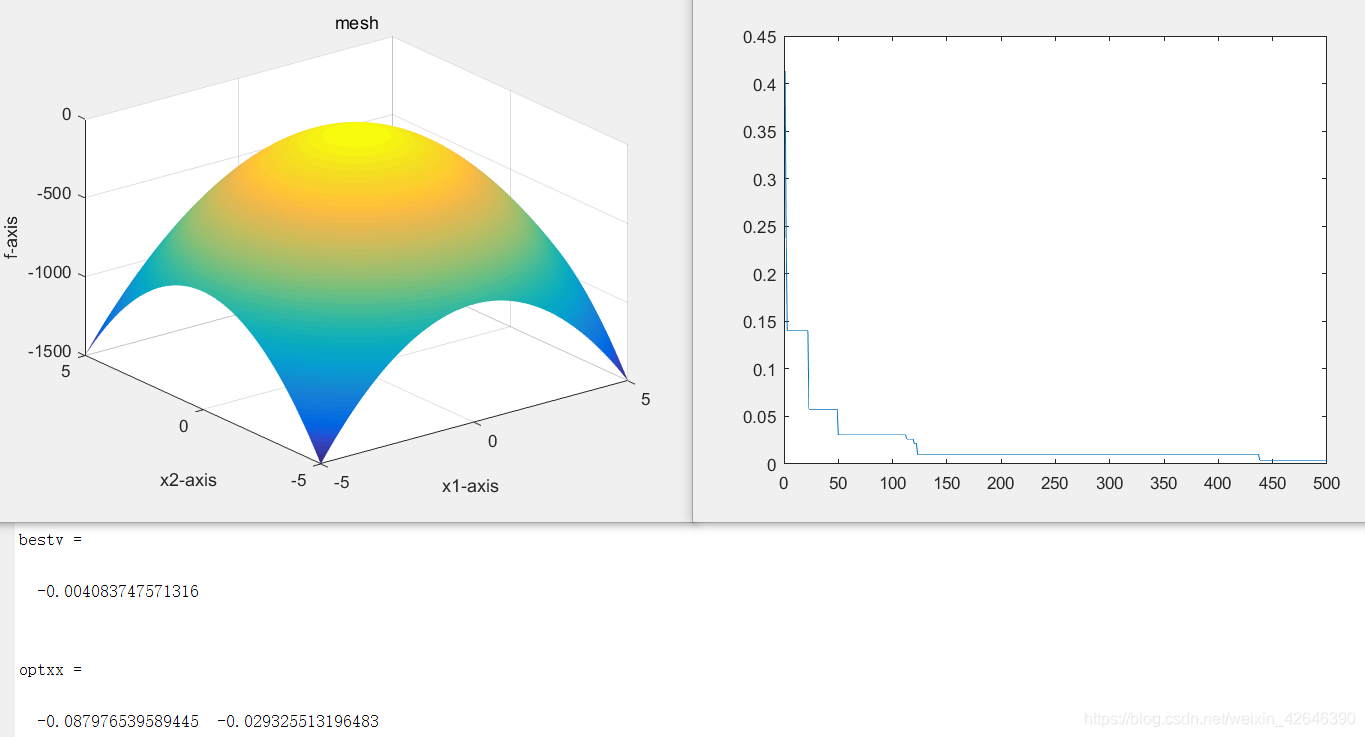
当种群数量为30时，结果如下：

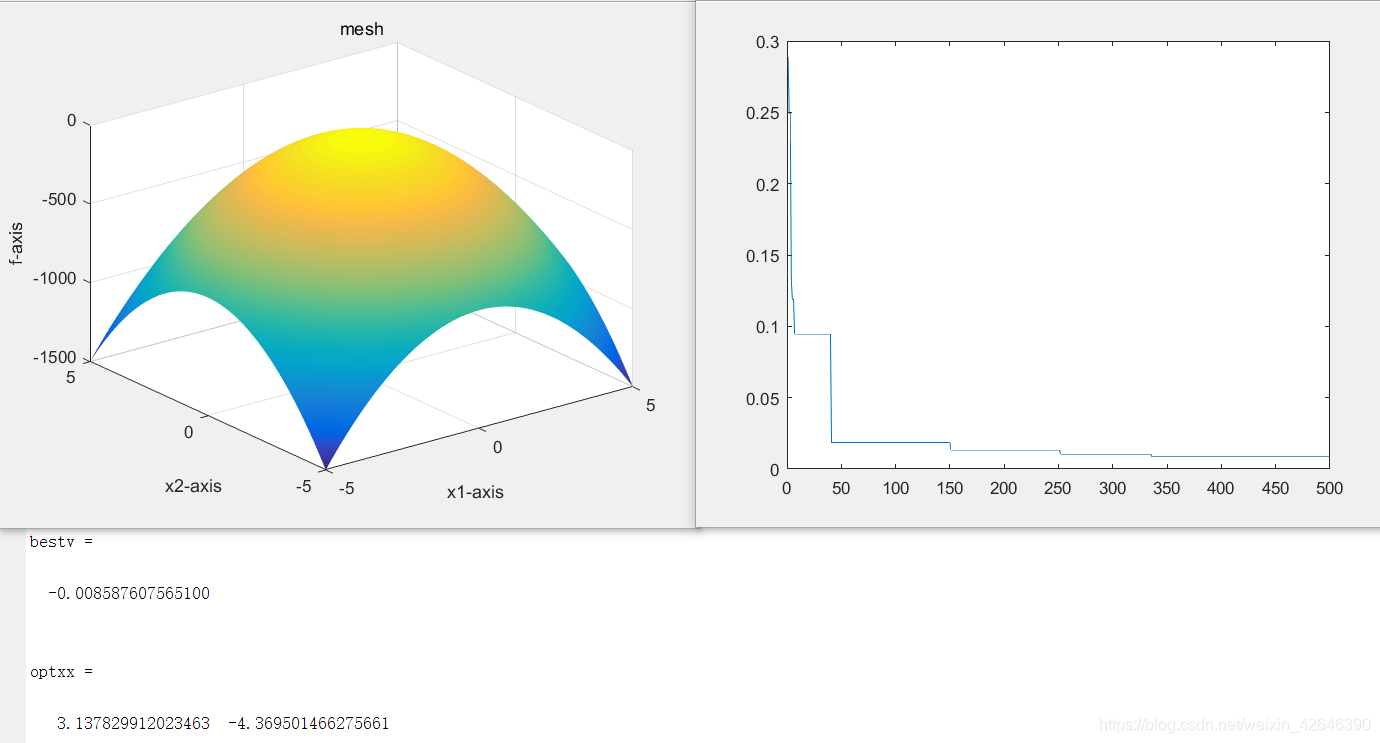
当种群数量为60时，结果如下：

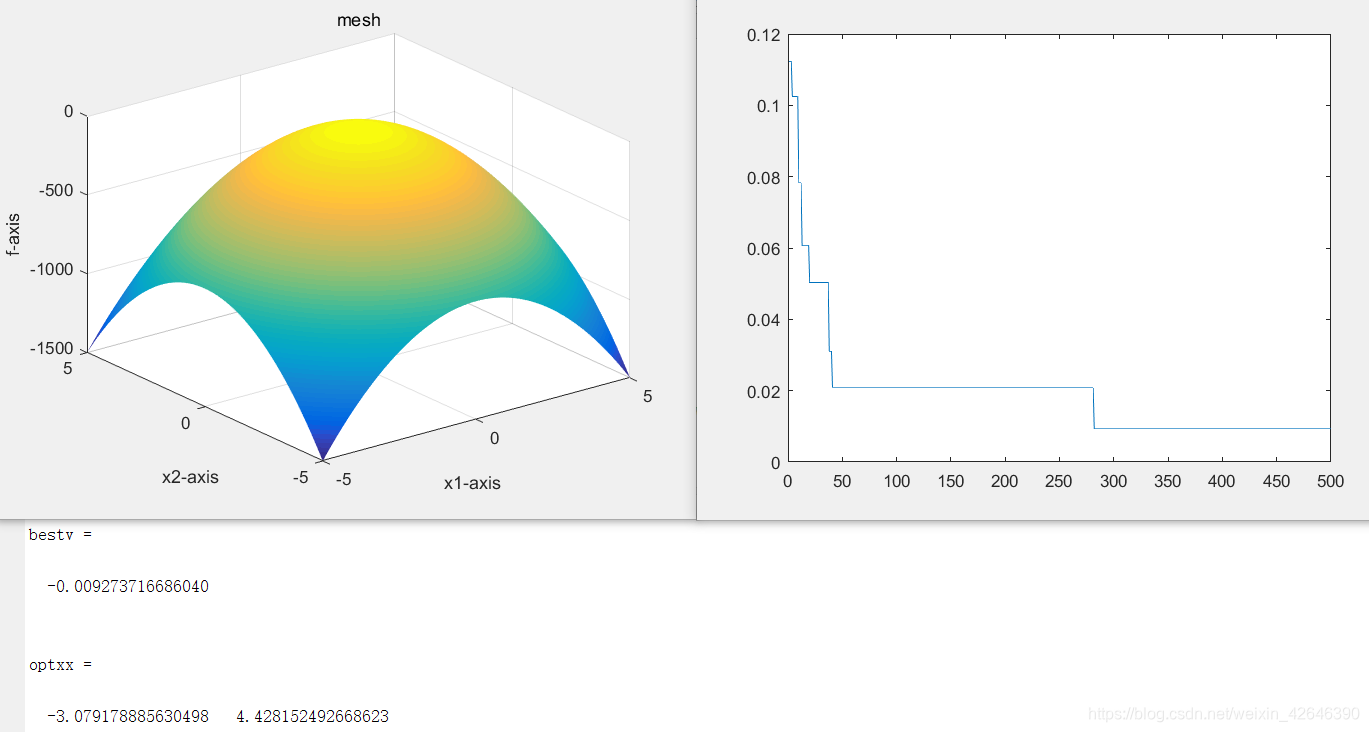
结果分析：当解空间维度不变时，随着种群数量的增加，最优适应度曲线到达平稳的迭代次数也逐渐减少，最优适应度不断减小。

3.3.2 种群数量为40不变，改变解空间维度
当解空间维度为5时，结果如下：

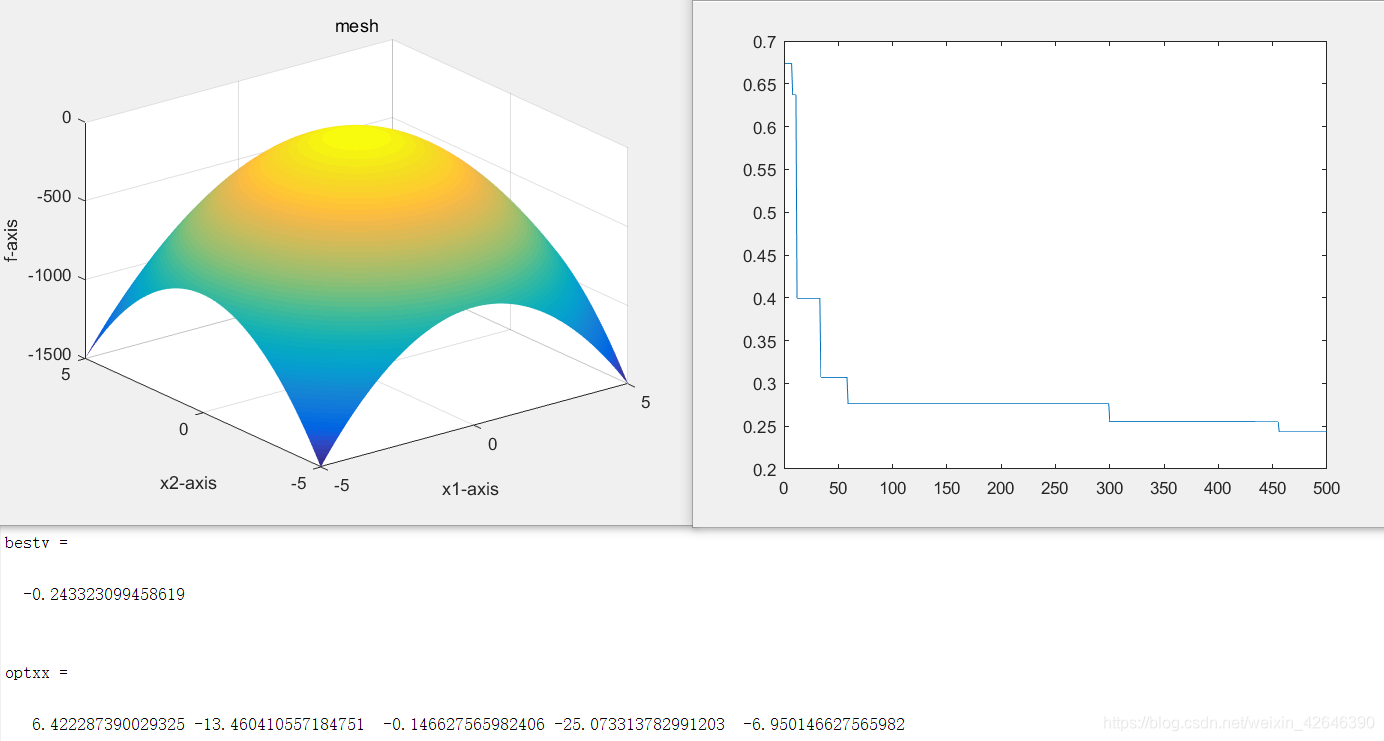
当解空间维度为10时，结果如下：

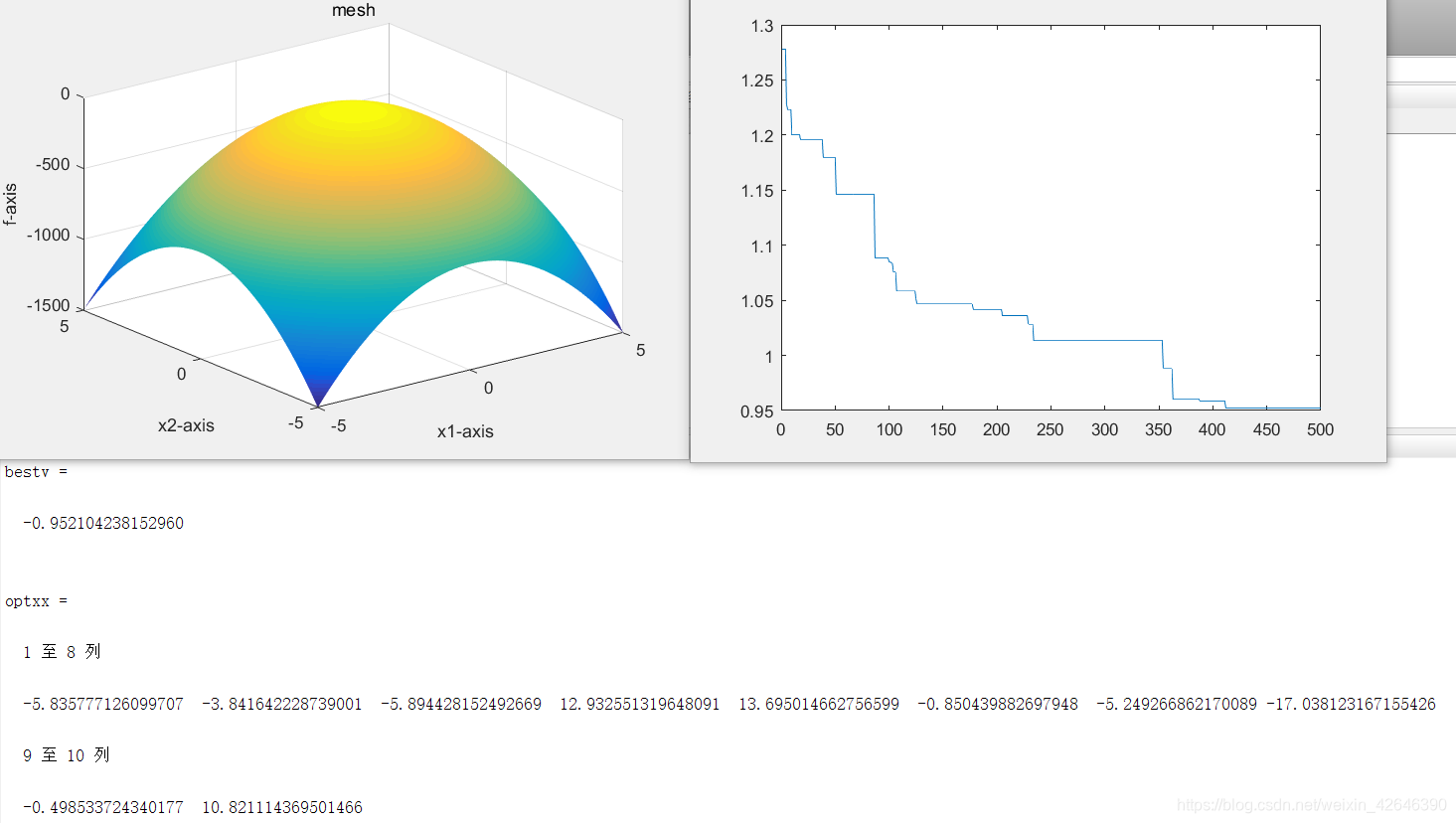
当解空间度为15时，结果如下：

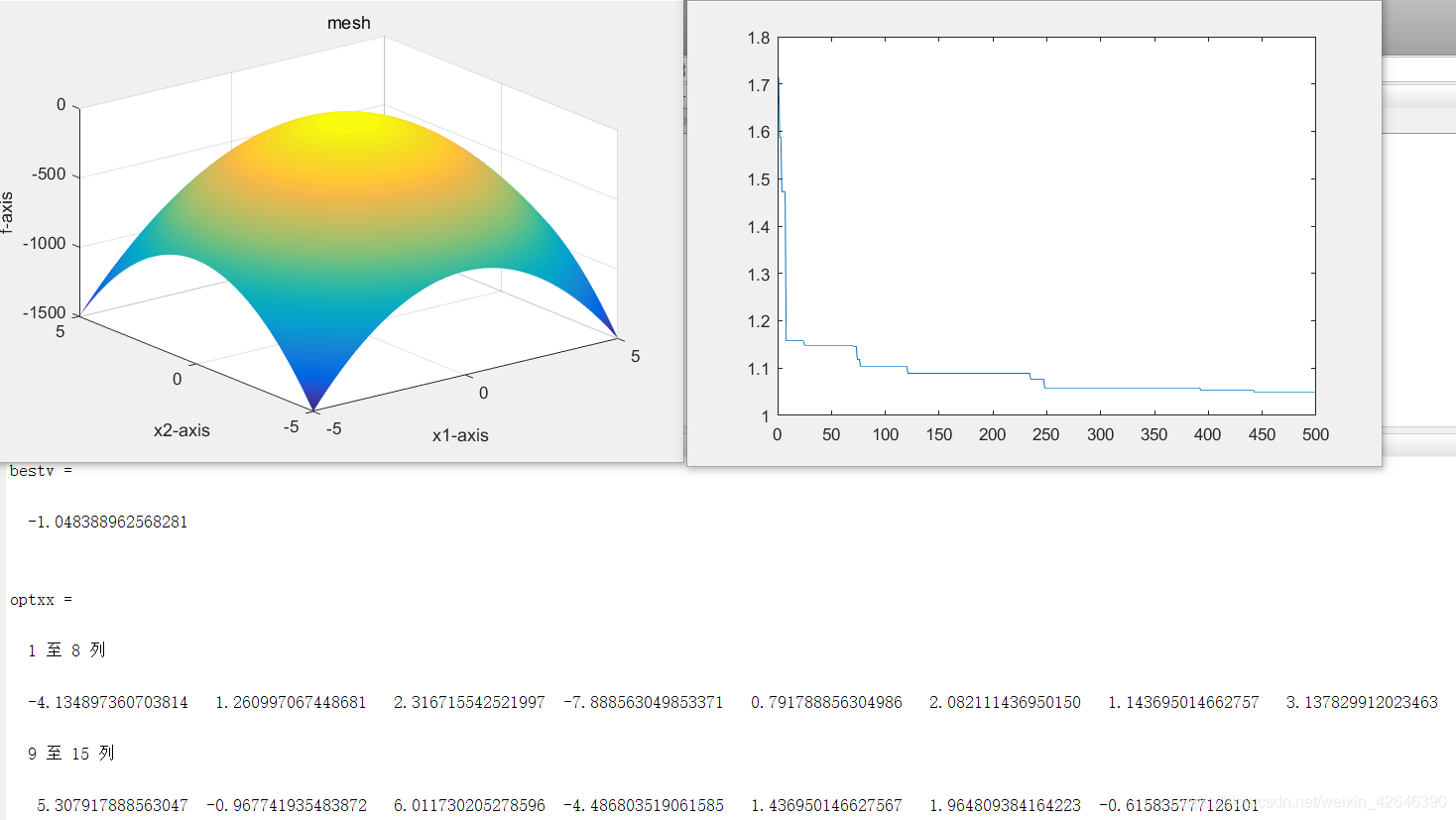
结果分析：当种群数量不变时，随着解空间维度的增大，最优适应度曲线到达平稳的迭代次数先减小后增大，最优适应度减小。

4.总结

• 对于Griewank函数，当解空间维度不变时，增加种群的数量，最优适应度会逐渐增大，精确度逐渐增大，但总体来说，种群变化对最优适应度的影响比较少。
• 对于Rastrigin函数，增大种群数量或者解空间维度，都会使最优适应度曲线到达平稳时的迭代次数减少，最优适应度的结果也更精确。
• 对于Sphere函数，当改变种群数量和解空间维度时，都会对最适应度和最优适应度曲线优影响，两者都增大时，最优适应度会减小。
• 在运行时间上，当种群数量不变时，增大解空间维度，运行时间增加，当解空间维度不变时，增加种群数量回事运行时间增大，
• 遗传算法时随机性的，每一次的运行结果都不相同。