我们为什么讨厌右半平面零点？如何避免和转化？

原创已于 2025-05-07 14:23:38 修改 · 2.7k 阅读

40 ·

CC 4.0 BY-SA版权

文章标签：

#平面

于 2025-01-24 15:57:27 首次发布

模拟IC设计专栏收录该内容

12 篇文章

订阅专栏

问题的前半部分——我们为什么讨厌右半平面零点，这个问题，最先让人好奇的是，为什么这个时候只讨论零点，而不讨论极点。原因是，讨论不了——如果极点位于右半平面，系统不收敛呀，不收敛系统就崩了······这属于复变函数的基本概念了。有些朋友可能已经忘记，此处放个图帮助朋友们回忆一下。

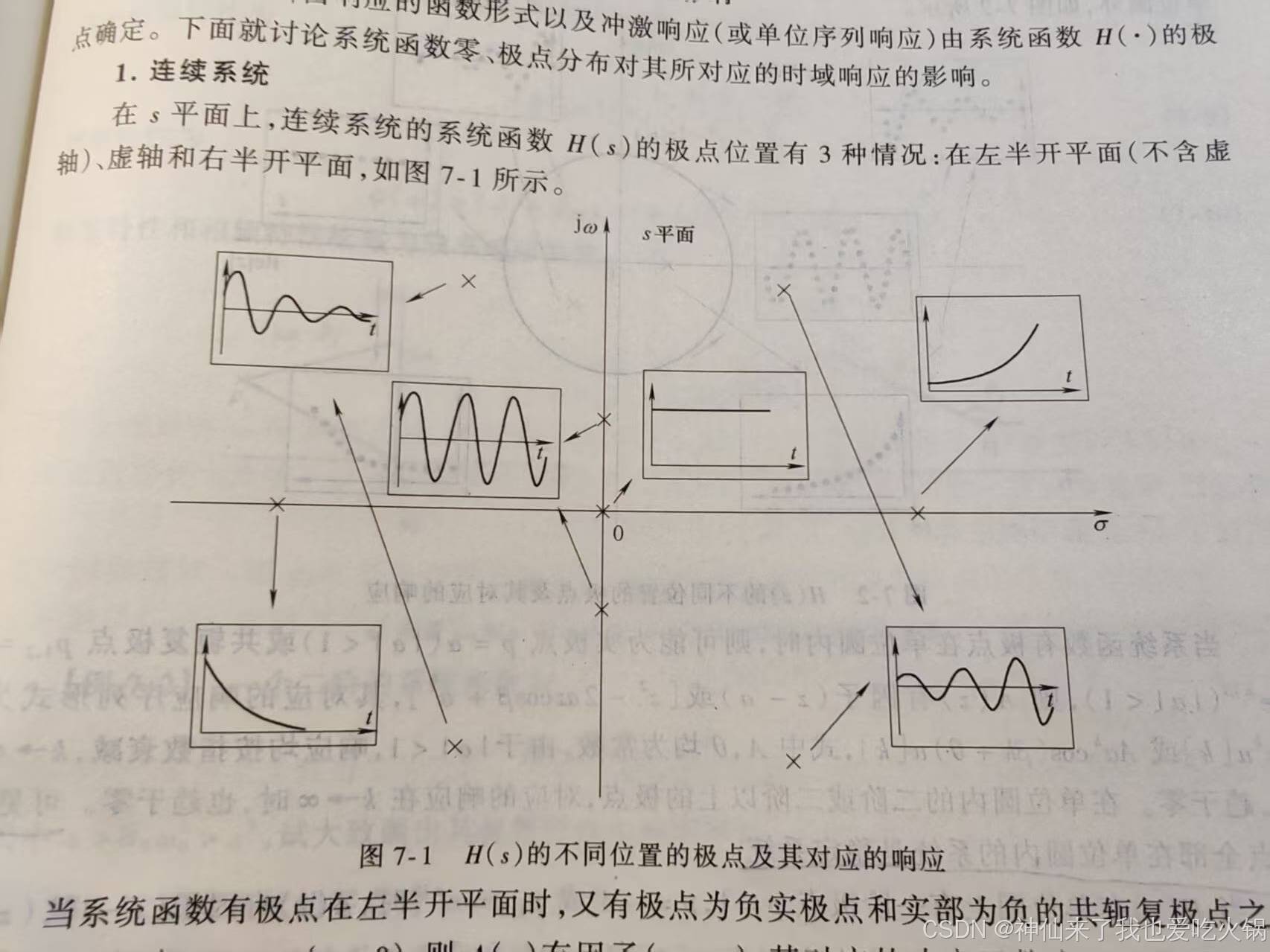
问题是右半平面的零点如何解释，此处，可以把频域的系统函数回归到时域。在频域的方程，一般很难直接窥视其物理意义。但是时域的方程是比较容易理解的。

假设一个二阶系统，共有两个极点-a和-b，|a|>|b|，也即b频率是主极点。一个零点-c。a、b、c的绝对值不相等。那么对应的频域系统函数方程应该是，

其中s参数的系数都是1，因为系数非1的情形一定可以化成这个方程的固定常数倍。写出上面方程式做拉普拉斯逆变换的过程，

则时域方程可以写成

其中，

联立解方程，有

也即时域方程可以写成

现在就可以观察，零点在左半平面和右半平面有什么区别了。

这个时候，可以注意到，a、b、c三个参数的大小则极大地影响到了函数的效果。按照前文，已经设定了极点是-a、-b，且，也即-b是主极点了。这时候，c有三种情况，我先用表列举一下，以便于后续理解(请注意，a、b为正数，但是极点是-a和-b。c同理，当c为正数的时候，零点-c才处于左半平面。)：

	c的大小	物理意义	时域波形
情形1	c<0	零点处于右半平面，	向下震荡
情形2	0<c<b	零点处于左半平面，角频率值比最小的极点角频率数值还小	向下震荡
情形3	b<c<a	零点处于左半平面，角频率值，比最小的极点角频率数值大，比非主极点角频率数值小	单调收敛
情形4	c>a	零点处于左半平面，角频率值，比非主极点角频率数值大	向上震荡

此时，不如尝试直接给予abc对应的值，进行Matlab仿真画图就行了。真实的角频率值，往往数值很大，比如1G。这样的话，函数不太好看——动不动就把时间压缩到ns以内了。所以选取一般值就行。此处先令a=110，b=10。

情形1：c<0时，假设为-10，绘制在左侧。右侧是多画了几根线，从-1000到-10000。

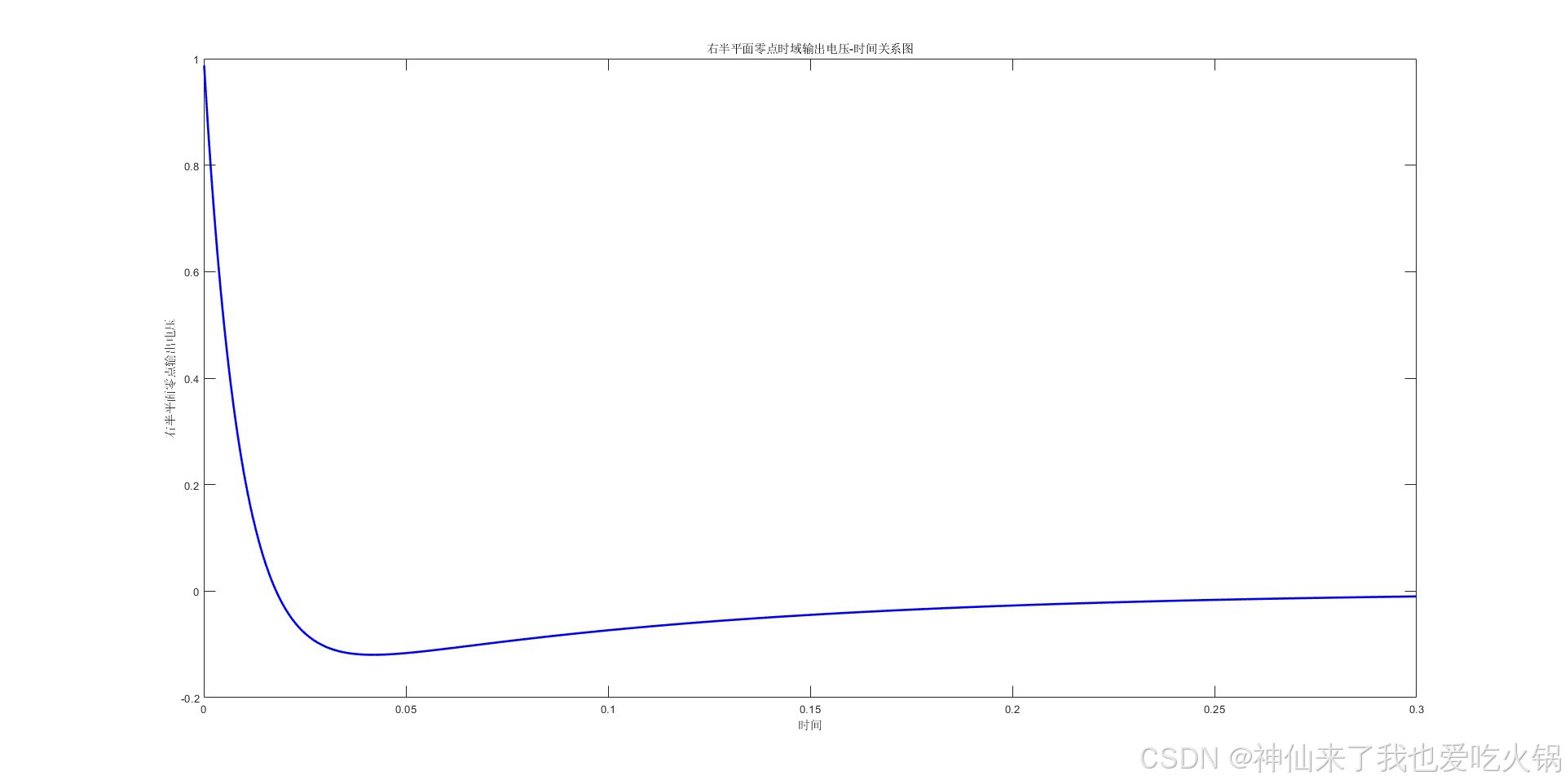
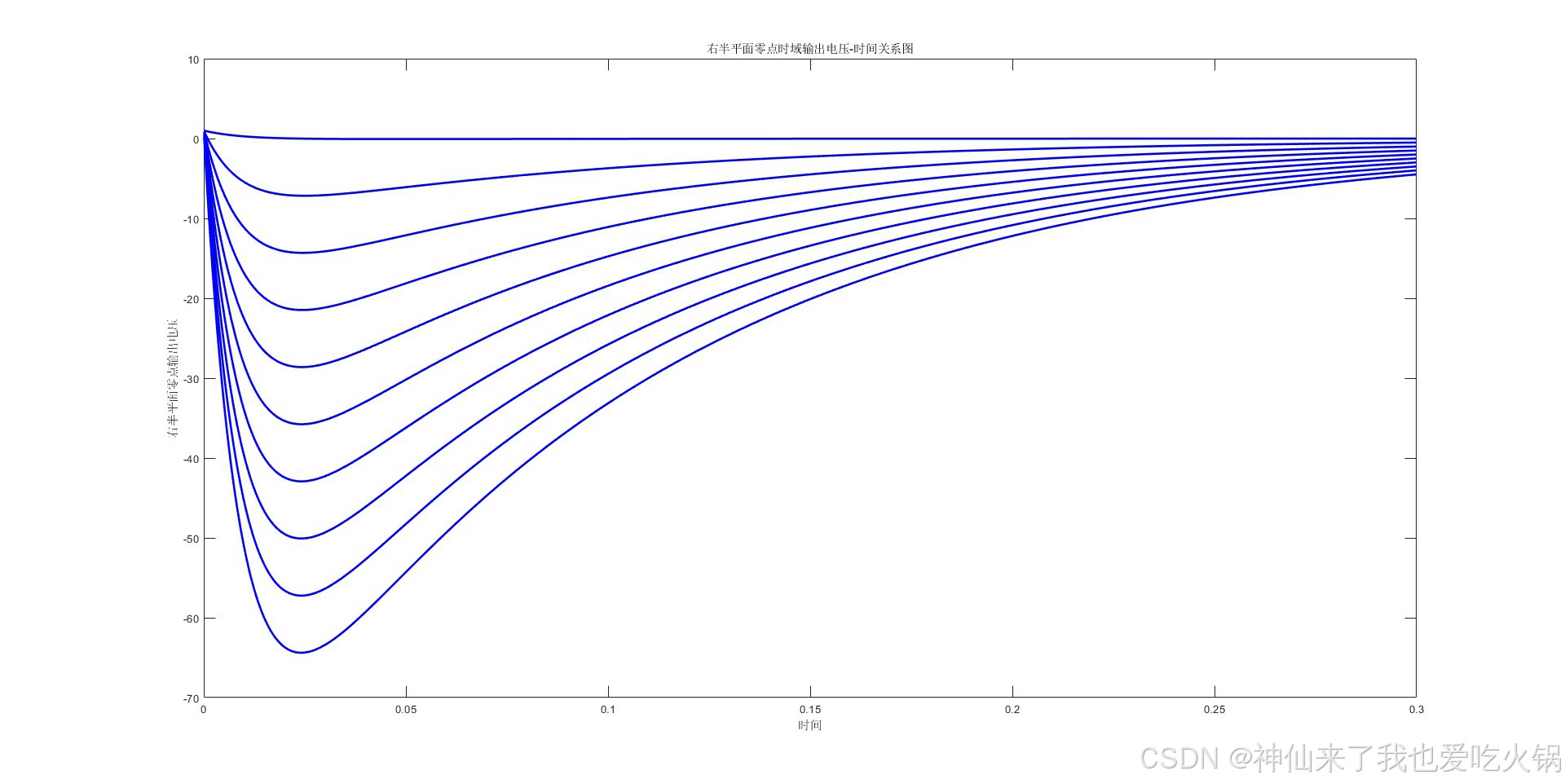
0<c<b时，假设为5，绘制在左侧。右侧是多画了几根线，从1到10。

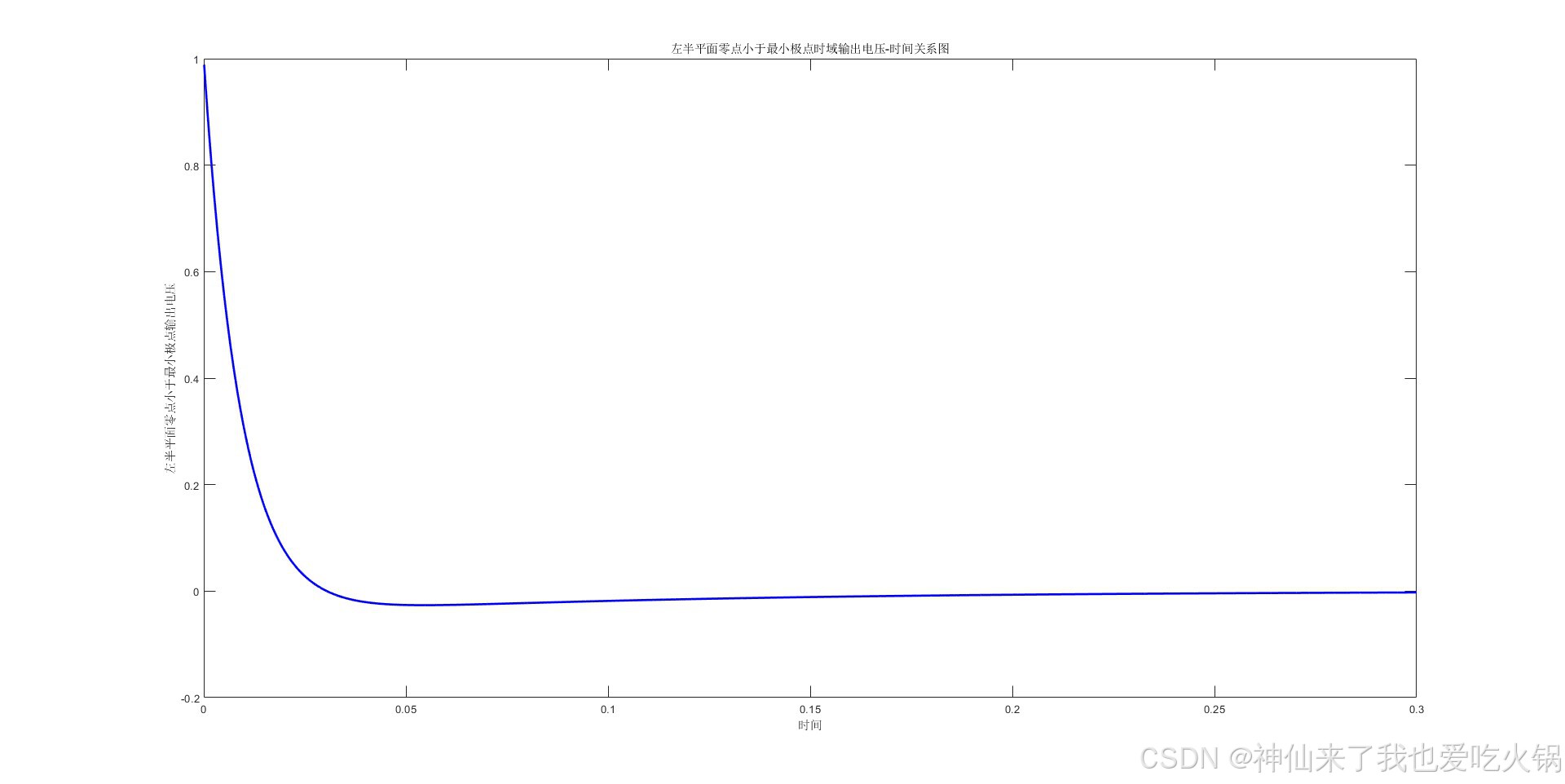
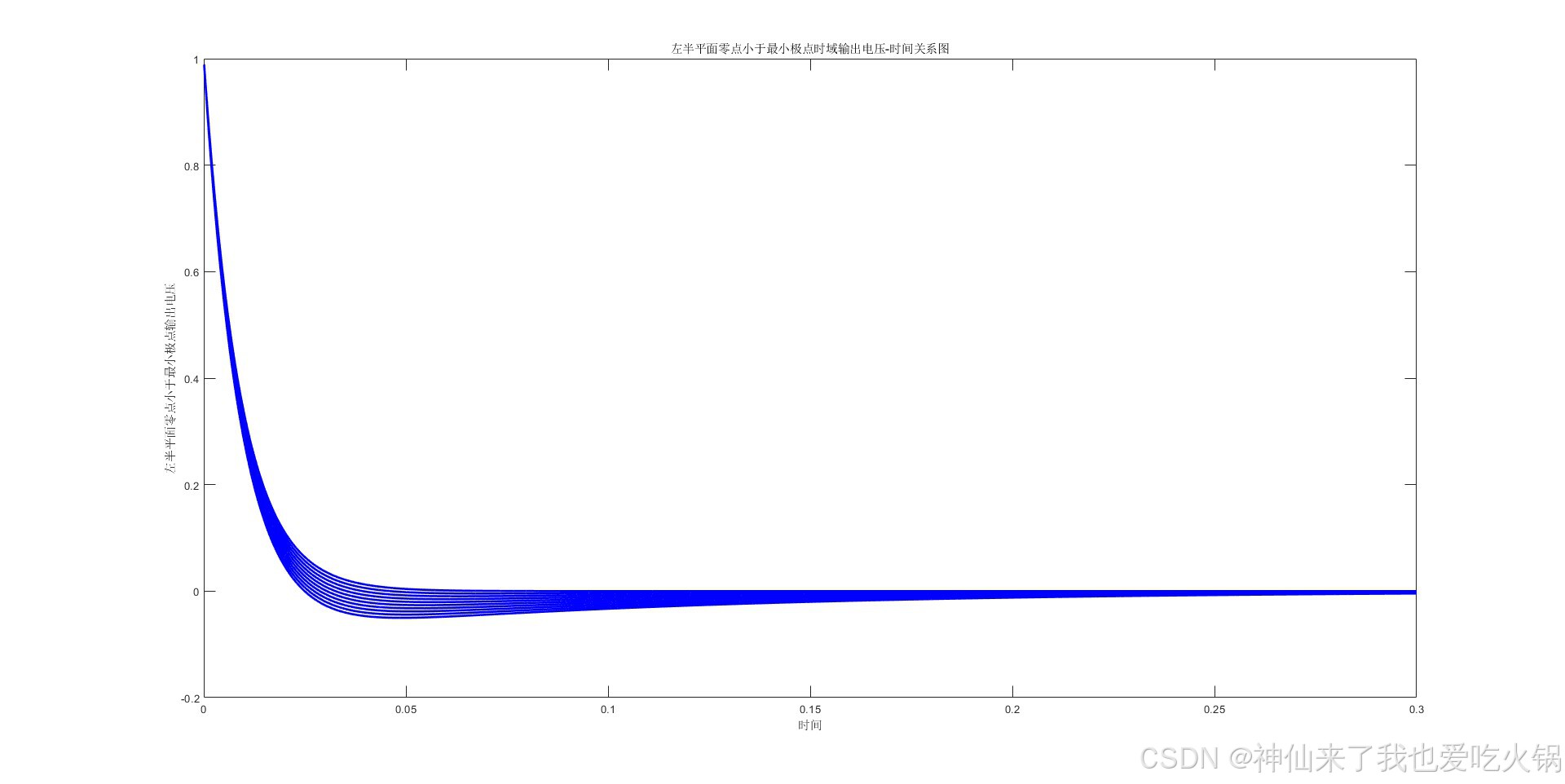
b<c<a时，假设为50，绘制在左侧。右侧是多画了几根线，从10到100。其实从公式中，已经很清晰了，这个时候时域信号归于正常。不再有信号冲击到0下的风险。

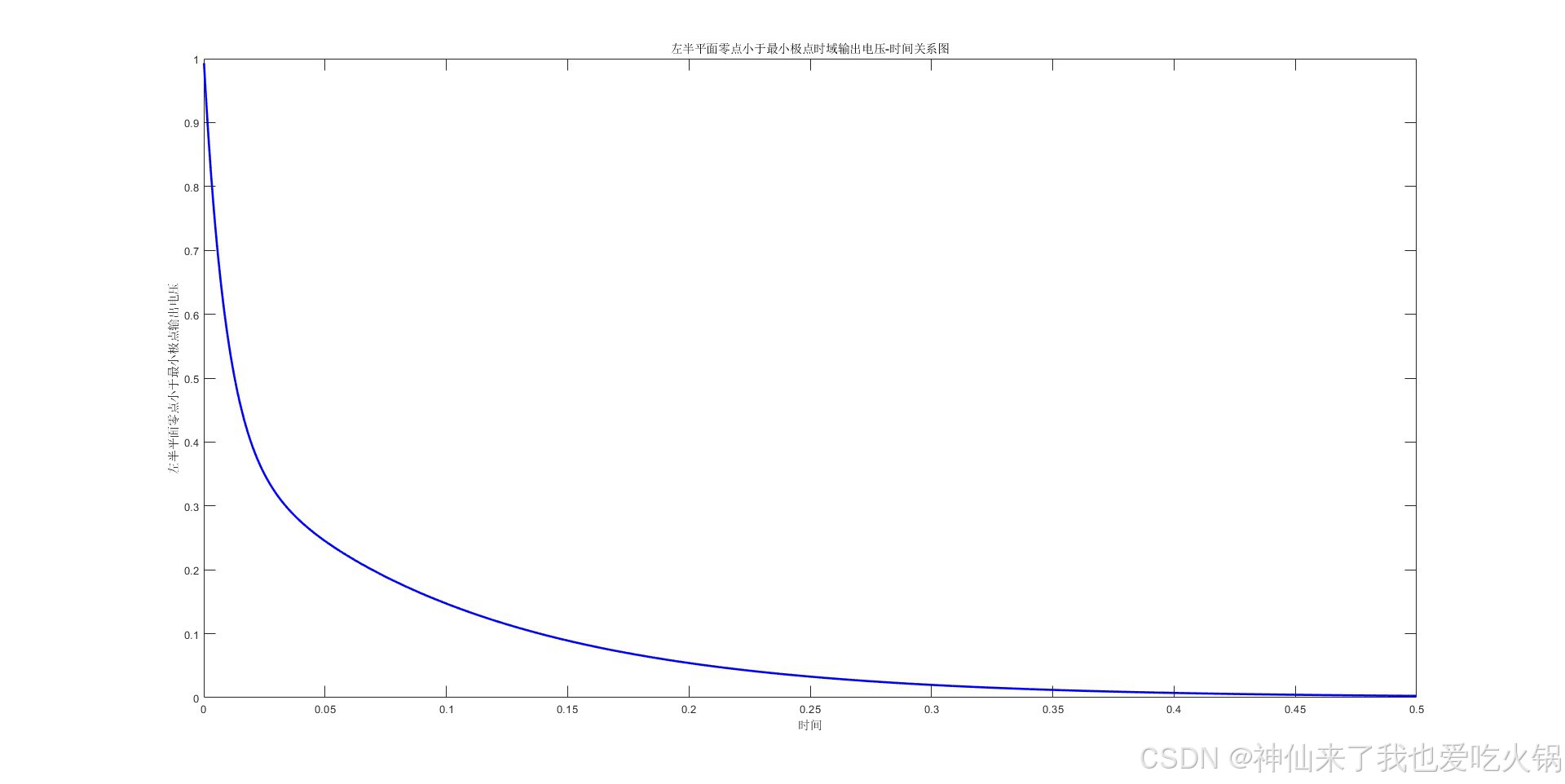
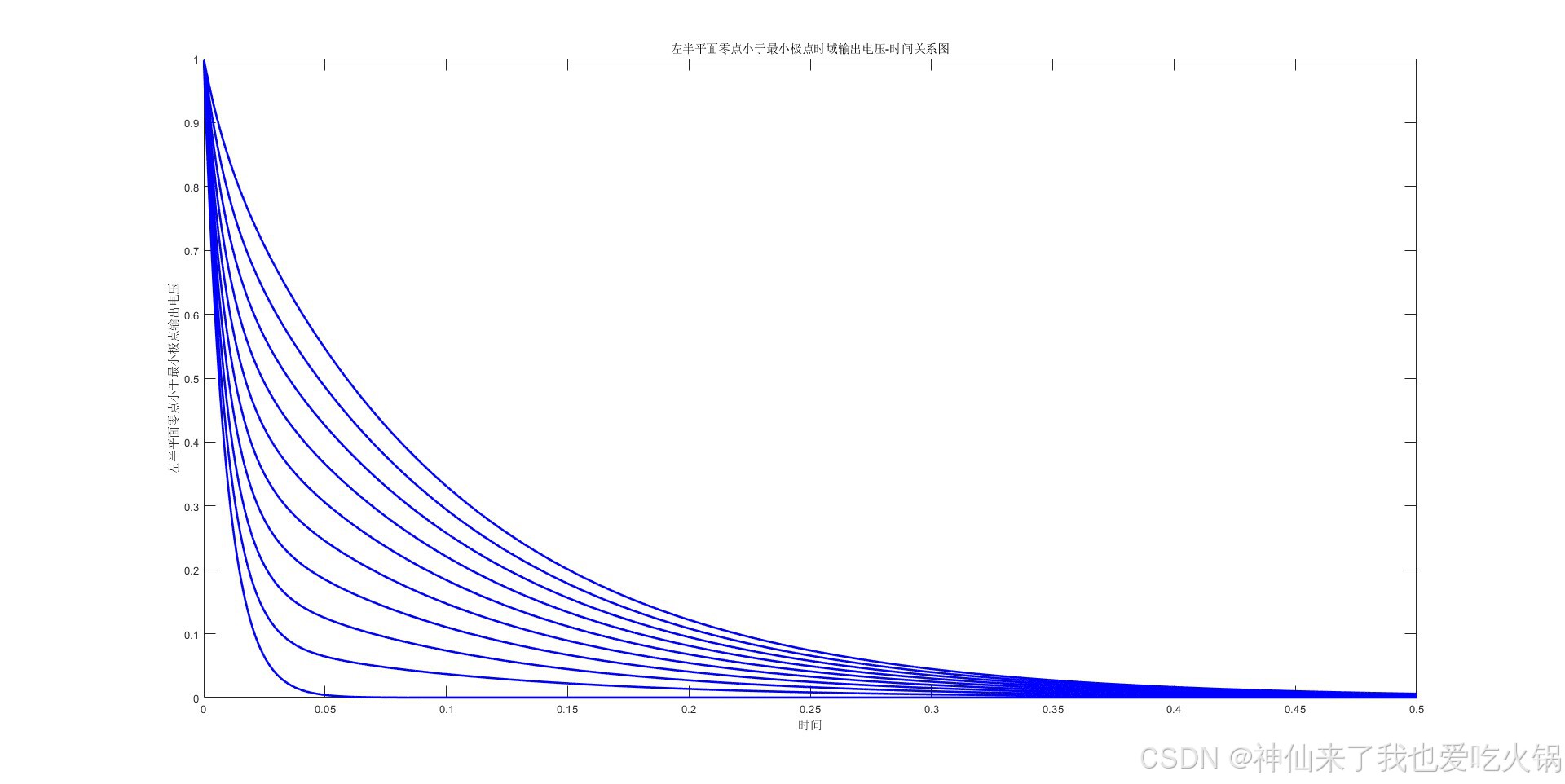
a<c时，假设为210，绘制在左侧。右侧是多画了几根线，从110到10110。

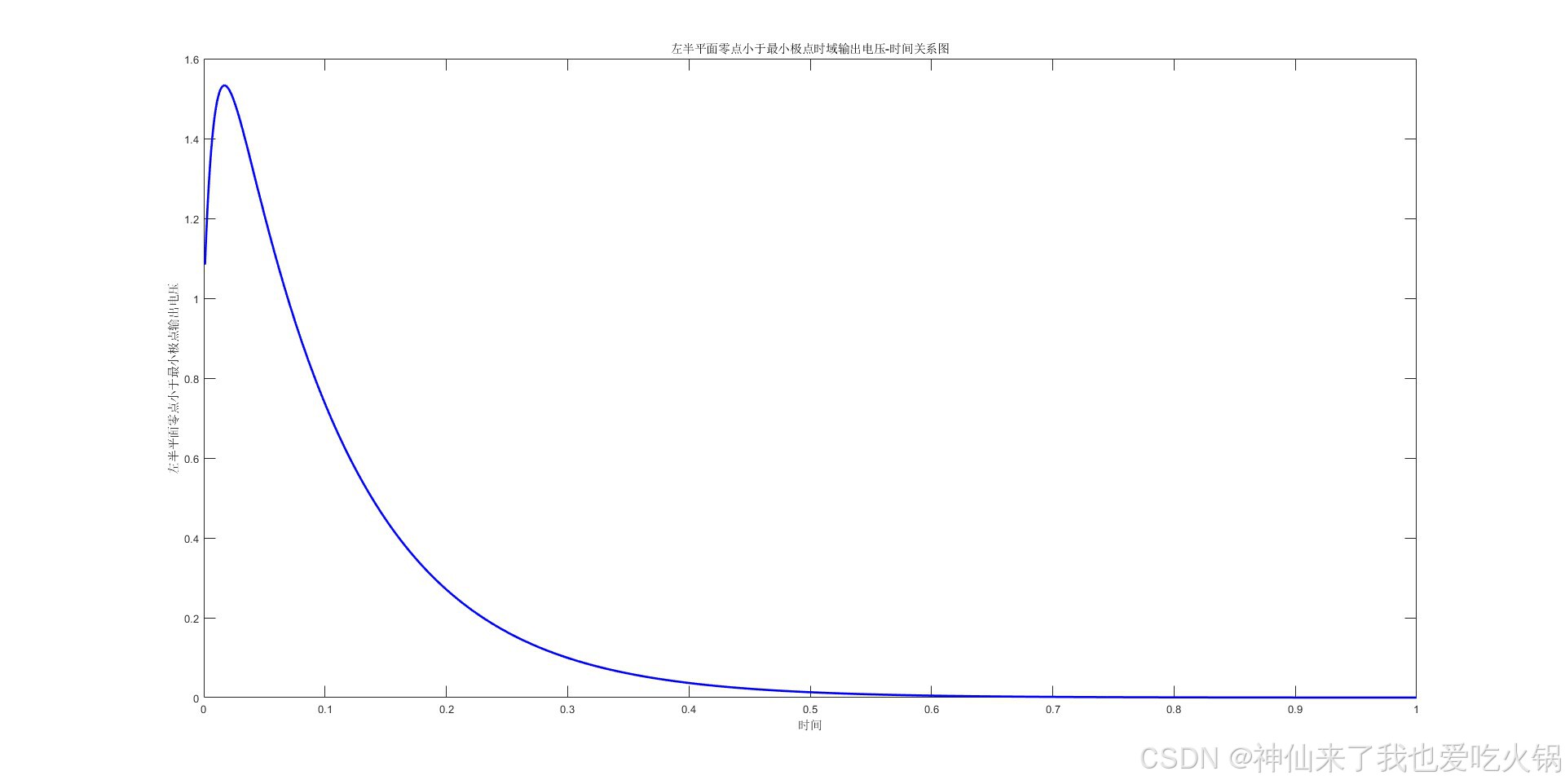
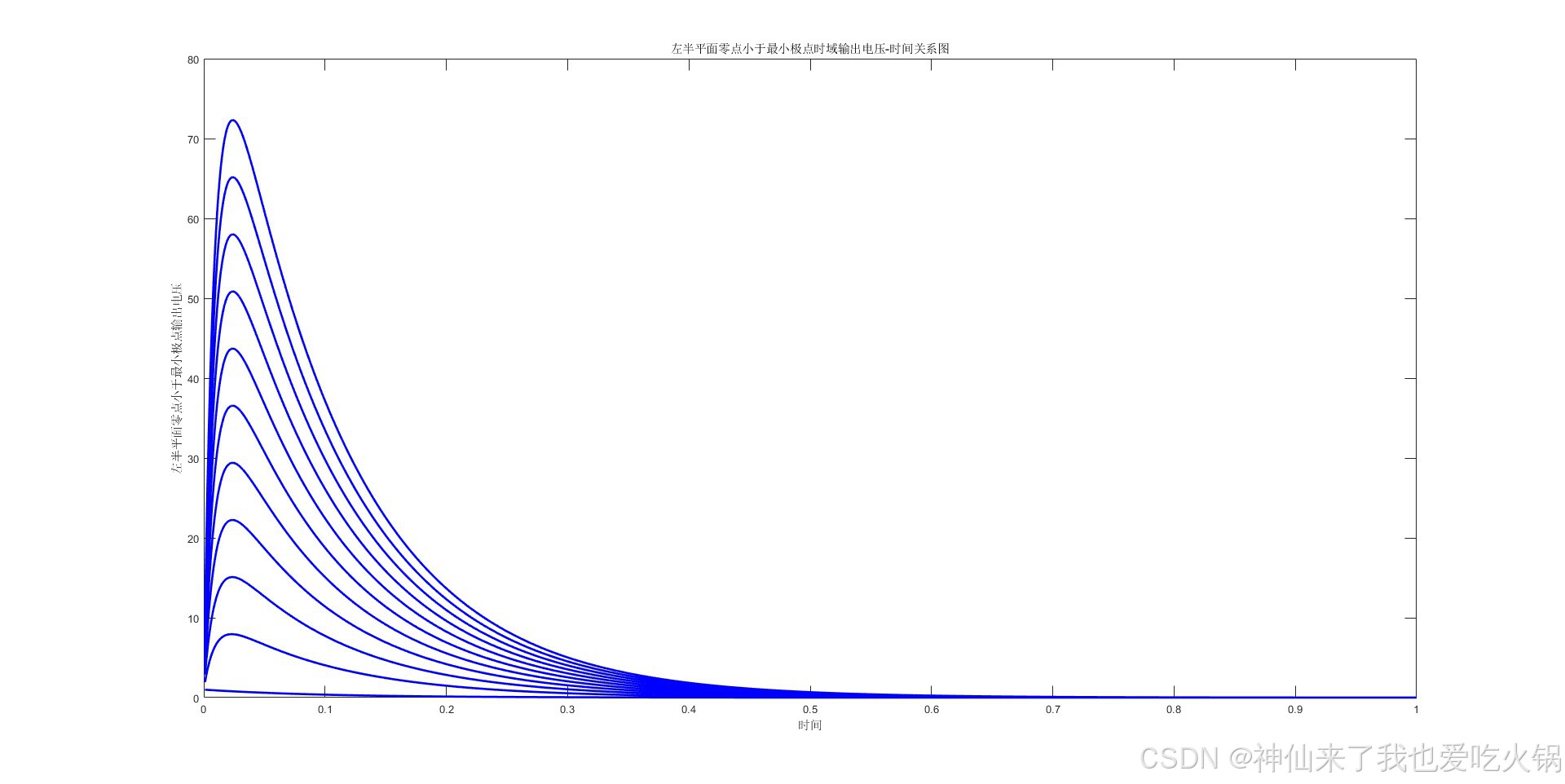
以上只是给了个感觉，可见

①零点在右半平面，信号向下震荡；

②零点在左半平面，且频率大于非主极点，信号向上震荡；

③零点在左半平面，且频率小于主极点，信号轻微向下震荡；

④零点在左半平面，且频率大于主极点，小于非主极点，信号完美收敛。

我有一篇博客中，写到了零点位于右半平面的物理意义——https://blog.youkuaiyun.com/weixin_42636352/article/details/143417006, 但是没说它有什么影响。如下图中，左侧则是零点在左半平面，右侧是零点在右半平面。电流方向相反，对于一个电容来说，我觉

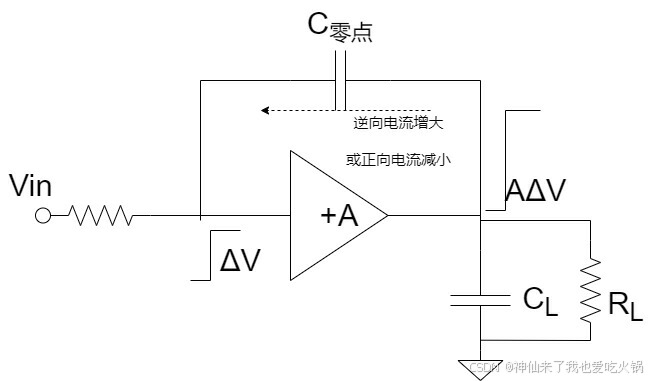
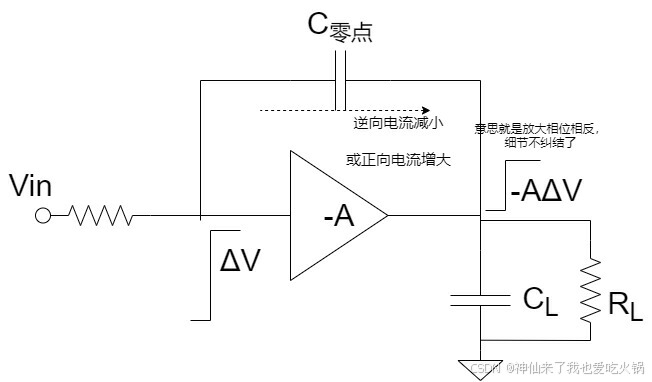
得可以直接理解为一个电容究竟当时是处于“被充电”还是“放电”。左半平面频率，和右半平面频率的区分，也就是充电频率和放电频率的区分——数值是通用的，只是电容的充放电方向不一样。当信号位于右半平面时，它与内部电流源电流方向相同了，这样子，它既不能抵消一部分Iload的大小，同时还直接把输入端的频率效应，直接通过米勒电容送到输出，这时候，米勒电容会充当了分摊Vin的分压的效果。这不是约等于触发极点了么。也即是，只要有右半平面零点，就相当于出现了一个左半平面极点。加上左半平面主极点，电路很快就震荡了。

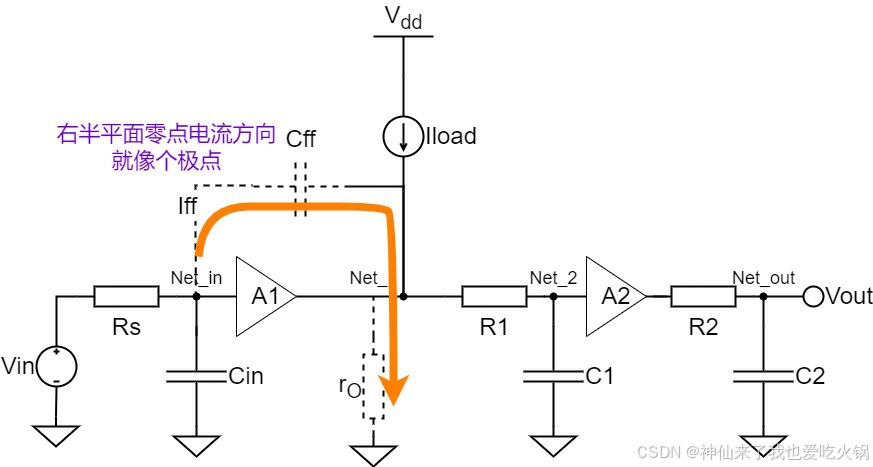
那如果是零点是左半平面，电流方向向左，最起码零点的电流，不会直接充当分摊Vin电压的效果。且根据基尔霍夫电流定律，如果，Cff上的电流，部分地抵消掉Cin的分摊效果，反而会减少极点的影响。也即零点和极点相抵消了。

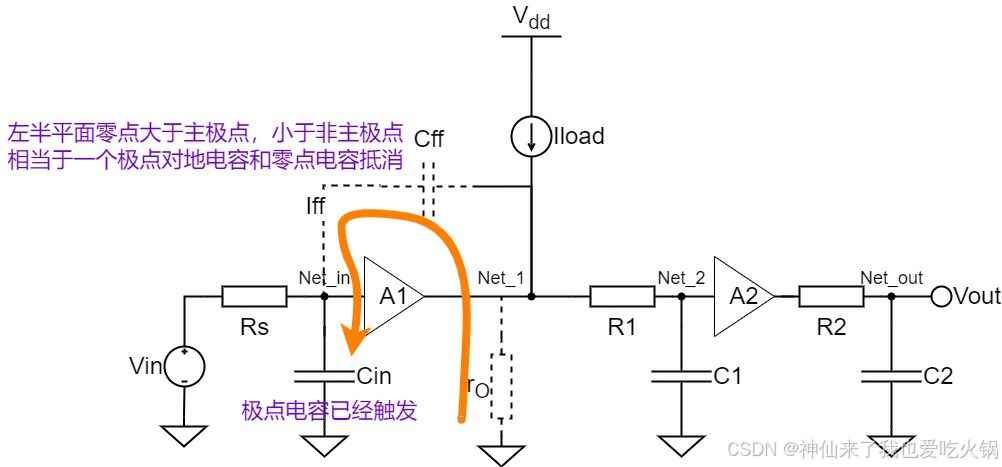
当然这个抵消也不能乱抵消，最起码要在主极点发生过后，如果是零点频率，虽然在左半平面，但是比主极点的频率还小，这时候，主极点还没发生，零点频率触发了，这时候Cff上有电流回流，必然会导致Rs上产生反向电流，导致输入向上线性增加了。

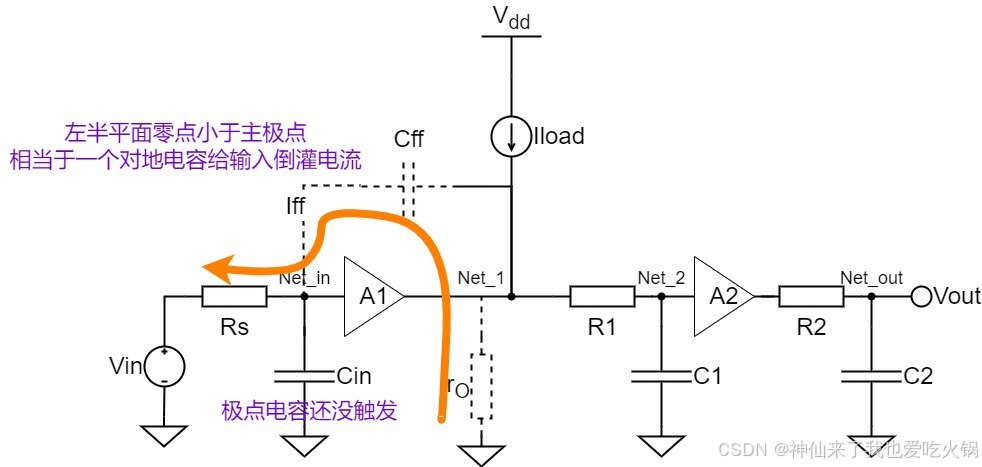
如果是零点频率，虽然在左半平面，但是比非主极点的频率还大，和上一段发生的情况一样，Cin上反灌的电流已经饱和了，会给Rs倒灌电流，只是，频率都大于非主极点了，到了系统应用的带宽之外，你爱咋咋地。

怎么避免和转化：方案比较教条，这部分我直接简化抄录一部分书上的内容了，有兴趣的朋友，可以阅读林康·莫莱大神的《模拟集成电路设计——以LDO设计为例（第2版）》，书中的6.5.3节。在这里的介绍里面，林康·莫莱老爷子，说了一个观点，就是他认为这种零点主要是因为米勒电容引起的，所以，提出的解决方案也都是针对米勒电容的。可是这样就有一个问题了呀，要是有寄生电容怎么办呢！林老爷子都不说，那我就更不会了。先忽略这里将就着看吧。

①在米勒电容位置插入一个电阻，将米勒电容位置引入的右半平面零点移动到无穷远处。先看图：

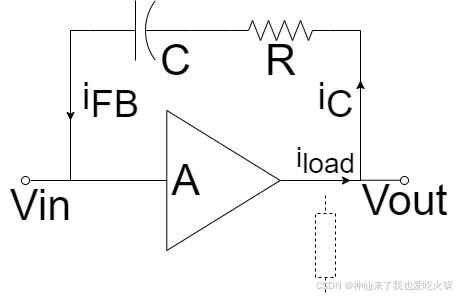
在上面的图中，一般情况下，零点的发生是和相互抵消，虚线绘制的电阻的影响我先忽略了。因为，的变小，假设没有电阻的话，其实就等同于将变大，也即把零点无限向远处推了。在我的眼中，这个方案执行难度比较大，因为当R大到一定程度的时候，电路会倒相。且R的限制值并不大，所以要设计这么小一个电阻值是不容易的。具体数值见下文。

②利用电阻将零点的极性反转，从右半平面到左半平面。如上面的图，可以得到，零点的发生条件是

令

可以解出来，

从图中可以看出来，当的时候，零点倒相到左半平面。当然为了抵消极点，肯定还得设计数值了。现在你就说倒相没倒相吧。

③利用放大（缓冲）器，将零点彻底消除。这个方法，在我眼中，其实只是上面两种方法的继续延续而已。所谓的放大（缓冲）器，其实就是把电阻R的阻值拉到无穷大。放大（缓冲）器可以使用电压放大（缓冲）器，电流放大（缓冲）器，多倍电流放大器共三个方案。分别的图形我直接一股脑儿画在下面：

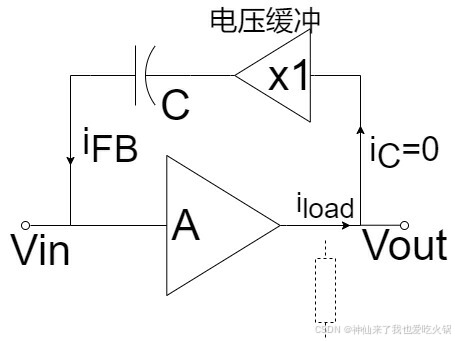
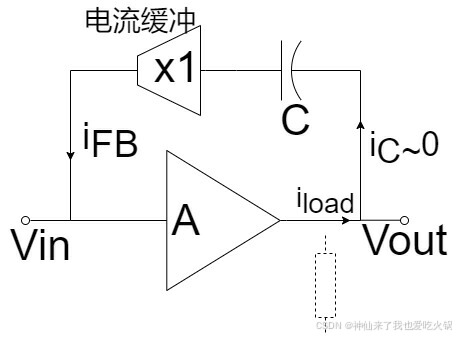
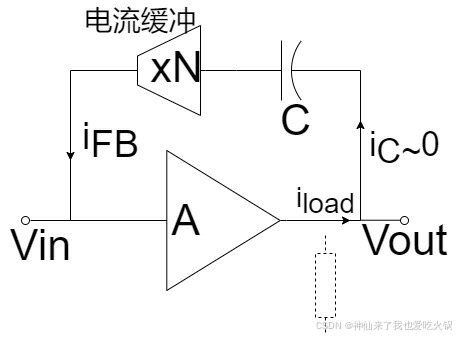
道理都一个，使用这种缓冲模式的时候，在输入端的不会受太大影响，可是输出端的几乎消失了，也即永远不会有一个前后贯通的电流，抵消，也即零点不会发生。这里值得注意的一点是电压缓冲，可以直接到0，而电流缓冲的话，会繁琐一点，电流缓冲可以说只是提供了一个超大的阻抗，但不是理想无穷大，所以，电流缓冲倍数越大（电流镜），则需求的越小，也即消除零点越彻底。那么这种电流缓冲的电路有什么意义呢？我也不知道。估计就是林老爷子为了保证叙述的完整性吧。