迪杰斯特拉（dijkstra）算法

上图

 

核心

		// 核心算法
		for (int i = 2; i <= n; i++) { // 要加入n-1顶点
			
			// 找距离原点最近的顶点
			min = Integer.MAX_VALUE;
			for (int j = 1; j <= n; j++) {
				if (book[j] == 0 && dis[j] < min) {
					min = dis[j];
					u = j;
				}
			}
			book[u] = 1;
			
			// 以u为中间点，修正各点之间的距离
			for (int k = 1; k <= n; k++) {
				if (e[u][k] < Integer.MAX_VALUE && dis[u] + e[u][k] < dis[k]) { 
					dis[k] = dis[u] + e[u][k]; //更新最短距离
					path[k] = u;
				}
			}
			
		}

全部代码

import java.util.Deque;
import java.util.LinkedList;
import java.util.Scanner;

/**
 * 迪杰斯特拉算法
 * @author Administrator
 *
 */
public class TestDijkstra {

	public static void main(String[] args) {
		Scanner input = new Scanner(System.in);
		int n, // 顶点
			m, // 边
			t1, t2, t3;
		n = input.nextInt();
		m = input.nextInt();

		int[][] e = new int[n + 1][n + 1]; // 路径
		
		// 初始化
		for (int i = 1; i <= n; i++) {
			for (int j = 1; j <= n; j++) {
				if (i == j) {
					e[i][j] = 0;
				} else {
					e[i][j] = Integer.MAX_VALUE;
				}
			}
		}
		
		// 读入边
		for (int i = 0; i < m; i++) {
			t1 = input.nextInt();
			t2 = input.nextInt();
			t3 = input.nextInt();
			
			e[t1][t2] = t3;
		}
		
		dijkstra(n, e);
		
		if (input != null) {
			input.close();
		}
		
	}
	
	/**
	 * dijkstra算法
	 * @param n 顶点数
	 * @param e 图的邻接矩阵
	 */
	public static void dijkstra(int n, int[][] e) {
		int  min, u = 0;
		int[] dis = new int[n + 1], // 到各个顶点的最短距离
			  book = new int[n + 1], // 判断顶点是否S集合中
		      path = new int[n + 1]; // 记录前一个顶点
		
		// 初始化dis、book
		for (int i = 1; i <= n; i++) {
			dis[i] = e[1][i];
			book[i] = 0;
			path[i] = 1;
		}
		book[1] = 1;
		
		// 核心算法
		for (int i = 2; i <= n; i++) { // 要加入n-1顶点
			
			// 找距离原点最近的顶点
			min = Integer.MAX_VALUE;
			for (int j = 1; j <= n; j++) {
				if (book[j] == 0 && dis[j] < min) {
					min = dis[j];
					u = j;
				}
			}
			book[u] = 1;
			
			// 以u为中间点，修正各点之间的距离
			for (int k = 1; k <= n; k++) {
				if (e[u][k] < Integer.MAX_VALUE && dis[u] + e[u][k] < dis[k]) { 
					dis[k] = dis[u] + e[u][k]; //更新最短距离
					path[k] = u;
				}
			}
			
		}
		
		// 打印结果
		display(n, dis, path);
		
	}
	
	/**
	 * 打印结果
	 * @param n 定点数
	 * @param dis 到各个顶点的最短距离
	 * @param path 记录前一个顶点
	 */
	public static void display(int n, int[] dis, int[] path) {
		System.out.println("顶点" + 1 + "到其他顶点的最短距离");
		
		for (int i = 2; i <= n; i++) {
			System.out.print("顶点" + i + ": ");
			Deque stack = new LinkedList();
			stack.push(i);
			int cursor = path[i];
			while (true) {
				stack.push(cursor);
				if (cursor == 1) {
					break;
				}
				cursor = path[cursor];
			}
			while (!stack.isEmpty()) {
				System.out.print(stack.pop() + "  ");
			}
			System.out.println("距离为: " + dis[i]);
		}
			
	}

}

测试

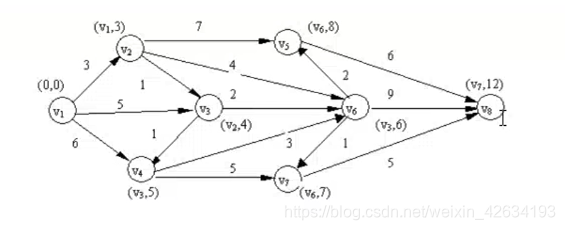
8 15
1 2 3
1 3 5
1 4 6
2 5 7
2 6 4
2 3 1
3 6 2
3 4 1
4 6 3
4 7 5
5 8 6
6 5 2
6 8 9
6 7 1
7 8 5

结果

顶点1到其他顶点的最短距离
顶点2: 1  2  距离为: 3
顶点3: 1  2  3  距离为: 4
顶点4: 1  2  3  4  距离为: 5
顶点5: 1  2  3  6  5  距离为: 8
顶点6: 1  2  3  6  距离为: 6
顶点7: 1  2  3  6  7  距离为: 7
顶点8: 1  2  3  6  7  8  距离为: 12