DirectX 12 3D游戏开发实战 （第二章 矩阵代数）

目录

矩阵代数

2.1　矩阵的定义

2.2　矩阵乘法

2.3　转置矩阵

2.4　单位矩阵

2.5　矩阵的行列式

2.6　伴随矩阵

2.7　逆矩阵

2.8　用DirectXMath库处理矩阵

---

矩阵代数

在计算机3D图形学中，我们利用矩阵简洁地描述几何体的变换，例如缩放、旋转和平移。除此之外，还可借助矩阵将点或向量的坐标在不同的标架之间进行转换。在本章中，我们将探索与矩阵有关的数学知识。

学习目标：

1．理解矩阵及其相关运算的定义。

2．探究为何能将向量与矩阵的乘法视为一种线性组合。

3．学习单位矩阵、转置矩阵、行列式以及矩阵的逆等概念。

4．逐步熟悉DirectXMath库中提供的关于矩阵计算的类与函数的子集。

2.1　矩阵的定义

一个规模为 m×n 的矩阵（matrix）M，是由m行n列实数所构成的矩形阵列。行数和列数的乘积表示了矩阵的维度。矩阵中的数字则称作元素（element）或元（entry）。通过双下标表示法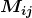指定元素的行和列就可以确定出对应的矩阵元素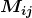，表示的是矩阵中第i行、第j列的元素。

例2.1

考察下列矩阵：

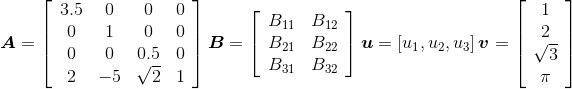
 1．A是一个4*4矩阵，B是一个3*2矩阵，u是一个1*3矩阵，v是一个4*1矩阵。

 2．我们通过双下标表示法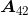=−5将矩阵A中第4行第2列的元素指定为−5，并以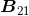表示B矩阵中第2行第1列的这一元素。

 3．u与v是两种特殊矩阵，分别只由一行元素或一列元素构成。由于它们常用于以矩阵的形式来表示一个向量（例如，我们可以自由地交替使用(x,y, z)与[x, y, z]这两种向量记法），因此有时候也分别称它们为行向量或列向量。观察可知，在表示行向量和列向量的矩阵元素时不必再采用双下标——使用单下标记法即可。

在某些情况下，我们倾向于把矩阵的每一行都看作一个向量。例如，可以把矩阵写作：

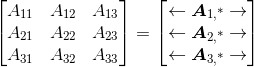
其中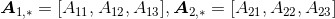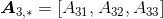，，。在这种表达方式中，第一个索引表示特定的行，第二个索引“*”表示该行的整个行向量。而且，对于矩阵的列也有类似的定义：

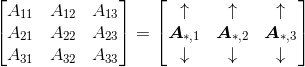
其中

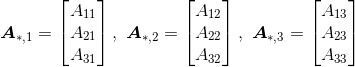
在这种表达方法中，第二个索引表示特定的列，第一个索引“*”表示该列的整个列向量。

现在来定义矩阵相等、加法运算、标量乘法运算和减法运算。

1．两个矩阵相等，当且仅当这两个矩阵的对应元素相等。为了加以比较，两者必有相同的行数和列数。

2．两个矩阵的加法运算，即将两者对应的元素相加。同理，只有行数和列数都分别相同的两个矩阵相加才有意义。

3．矩阵的标量乘法就是将一个标量依次与矩阵内的每个元素相乘。

4．利用矩阵的加法和标量乘法可以定义出矩阵的减法，即。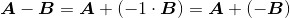

例2.2

设

那么，

（i）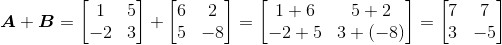

（ii）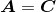

（iii）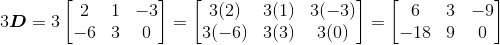

（iv）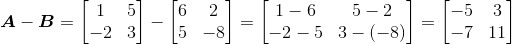

由于在矩阵的加法和标量乘法的运算过程中，是以元素为单位展开计算的，所以它们实际上也分别从实数运算中继承了下列性质：

1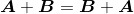．        加法交换律

2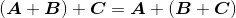．        加法结合律

3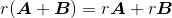．        标量乘法对矩阵加法的分配律

4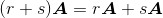．        矩阵乘法对标量加法的分配律

2.2　矩阵乘法

2.2.1　定义

如果A是一个m*n矩阵，B是一个n*p矩阵，那么，两者乘积AB的结果是一个规模为m*p的矩阵C。矩阵C中第i行、第j列的元素，由A矩阵的第i个行向量与B矩阵的第j个列向量的点积求得，即：

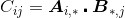
                                                                        （2.1） 

要注意的是，为了使矩阵乘积AB有意义，矩阵A中的列数与矩阵B中的行数必须相同。也就是说，矩阵A中行向量的维数（可认为是分量的个数）与矩阵B中列向量的维数要一致。如果二者的维数不同，那么式（2.1）中的点积运算没有意义。

例2.3

设

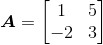                        ​​​​​​​           和  ​​​​​​​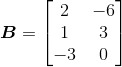

因为矩阵A的行向量维数为2，矩阵B的列向量维数为3，所以AB乘积无定义。不妨这样想，由于2D向量不能与3D向量进行点积计算，因此，矩阵A中的第一个行向量与矩阵B中的第一个列向量也就无法开展点积运算。

例2.4

设

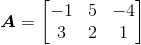        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​与​​​​​​​​​​​​​​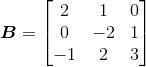

由于矩阵A的列数与矩阵B的行数相同，可首先指出乘积AB是有意义的（其结果是一个2*3矩阵）。根据式（2.1）可以得到：

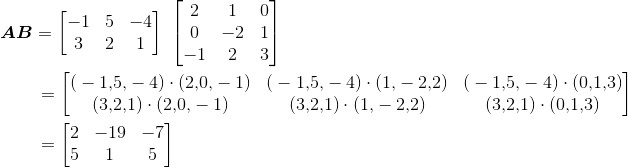
我们还可以发现乘积BA却没有意义，因为矩阵B的列数不等于矩阵A的行数。这表明，矩阵的乘法一般不满足交换律，即 AB ≠ BA。

2.2.2　向量与矩阵的乘法

        考虑下列向量与矩阵的乘法运算：

可以观察到：该例中，uA的计算结果是一个规模为1*3的行向量。现在运用式（2.1）即可得到：

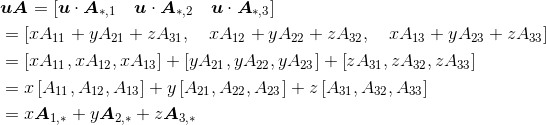
因此，

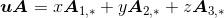
                                                                        （2.2） 

式（2.2）实为一种线性组合（linear combination），这意味着向量与矩阵的乘积uA就相当于：向量u给定的标量系数x、y、z与矩阵A中各行向量的线性组合。注意，尽管我们只展示了1*3行向量与3*3矩阵的乘法，但是这个结论却具有一般性。也就是说，对于一个1*n行向量u与一个n*m矩阵A，我们总可得到u所给出的标量系数与A中诸行向量的线性组合uA：

2.2.3　结合律

矩阵的乘法运算具有一些很有用的代数性质。例如，矩阵乘法对矩阵加法的分配律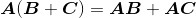以及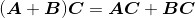。除此之外，我们还会不时地用到矩阵乘法的结合律，可借此来决定矩阵乘法的计算顺序：

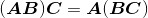
2.3　转置矩阵

转置矩阵（transpose matrix）指的是将原矩阵的行与列进行互换所得到的新矩阵。所以，根据一个m*n矩阵可得到一个规模为n*m的转置矩阵。我们将矩阵M的转置矩阵记作。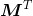

例2.5

求出下列3个矩阵的转置矩阵：

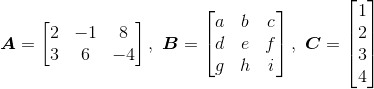
上面提到，通过互换矩阵的行和列来求出转置矩阵，于是得到：

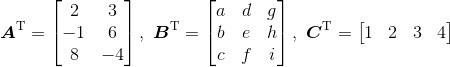
转置矩阵具有下列实用性质：

1．

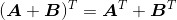
2．

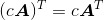
3．

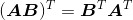
4．

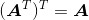
5．

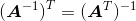
2.4　单位矩阵

单位矩阵（identity matrix）比较特殊，是一种主对角线上的元素均为1，其他元素都为0的方阵。

例如，下列依次是规模为2*2，3*3和4*4的单位矩阵：

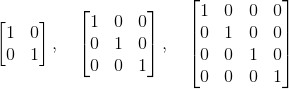
单位矩阵是矩阵的乘法单位元（multiplicative identity）。即如果A为m*n矩阵，B为n*p矩阵，而I为n*n的单位矩阵，那么

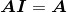        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​    且​​​​​​​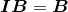

换句话说，任何矩阵与单位矩阵相乘，得到的依然是原矩阵。我们可以将单位矩阵看作是矩阵中的“数字1”。特别地，如果M是一个方阵，那么它与单位矩阵的乘法满足交换律：

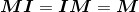
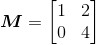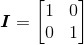设以及，证明。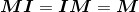

运用式（2.1）得：

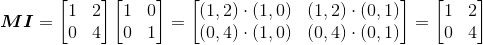
与

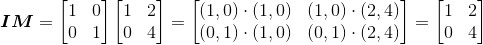
所以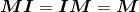是正确的。

例2.7

设u= [−1, 2]且。验证。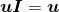

应用式（2.1），可得：

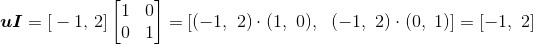
另外可以看出，我们无法计算乘积​​​​​​​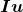，因为此矩阵乘法是无定义的。

2.5　矩阵的行列式

行列式是一种特殊的函数，它以一个方阵作为输入，并输出一个实数。方阵A的行列式通常表示为det A 。我们可以从几何的角度来解释行列式。行列式反映了在线性变换下，（n维多面体）体积变化的相关信息。另外，行列式也应用于解线性方程组的克莱姆法则（Cramer’s Rule，亦称克莱默法则）。然而，我们在此学习行列式的主要目的是：利用它推导出求逆矩阵的公式（第2.7节的主题）。此外，行列式还可以用于证明：方阵A是可逆的，当且仅当det A ≠ 0。这个结论很实用，因为它为我们确认矩阵的可逆性提供了一种行之有效的计算工具。不过在定义行列式之前，我们先要介绍一下余子阵的概念。

2.5.1　余子阵

指定一个n*n的矩阵A，余子阵（minor matrix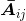）.即为从A中去除第i行和第j列的​​​​​​​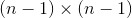矩阵。

求出下列矩阵的余子阵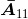、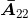和​​​​​​​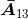

去除矩阵A的第一行和第一列，得到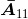为：

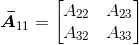
去除矩阵A的第二行和第二列，得到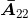为：

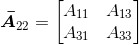
去除矩阵A的第一行和第三列，得到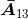为：

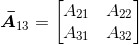
2.5.2　行列式的定义

矩阵的行列式有一种递归定义。例如，一个4*4矩阵的行列式要根据3*3矩阵的行列式来定义，而3*3矩阵的行列式要靠2*2矩阵的行列式来定义，最后，2*2矩阵的行列式则依赖于1*1矩阵的行列式来定义（1*1矩阵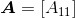的行列式被简单地定义为​​​​​​​）。

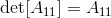设A为一个n*n矩阵。那么，当n>1时，我们定义：

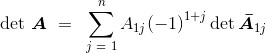
                                                                        （2.4）

对照余子阵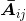的定义可知，对于2*2矩阵来说，其相应的行列式公式为：

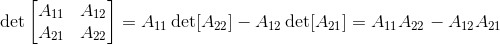
对于3*3矩阵来说，其行列式计算公式为：

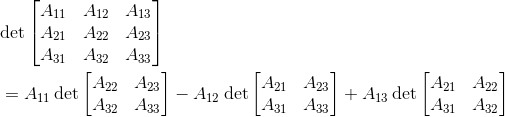
对于4*4矩阵，其行列式计算公式为：

在3D图形学中，主要使用4*4矩阵。因此，我们不再继续推导n>4的行列式公式。

例2.9

求矩阵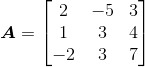的行列式。

我们有

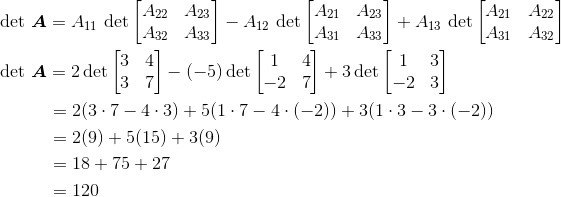
2.6　伴随矩阵

设A为一个n*n矩阵。乘积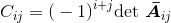称为元素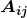的代数余子式（cofactor of  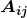）。如果为矩阵中的每个元素分别计算出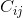，并将它置于矩阵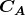中第i行、第j列的相应位置，那么将获得矩阵A的代数余子式矩阵（cofactor matrix of A）：

若取矩阵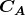的转置矩阵，将得到矩阵A的伴随矩阵（adjoint matrix of A），记作：

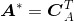
                                                                        （2.5）

在下一节中，我们将学习利用带有伴随矩阵的公式来计算逆矩阵。

2.7　逆矩阵

矩阵代数不存在除法运算的概念

，但是却另外定义了一种矩阵乘法的逆运算。下面总结了与矩阵逆运算有关的关键信息。

1．只有方阵才具有逆矩阵。因此，当提到逆矩阵时，我们便假设要处理的是一个方阵。

2．n*n矩阵M的逆也是一个n*n矩阵，并表示为。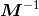

3．不是每个方阵都有逆矩阵。存在逆矩阵的方阵称为可逆矩阵（invertible matrix），不存在逆矩阵的方阵称作奇异矩阵（singular matrix）。

4．可逆矩阵的逆矩阵是唯一的。

5．矩阵与其逆矩阵相乘将得到单位方阵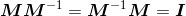：。可以发现，矩阵与其逆矩阵的乘法运算满足交换律。

另外，可以利用逆矩阵来解矩阵方程。例如，设矩阵方程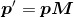，且已知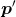与M，求p。假设矩阵M是可逆的（即存在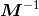），我们就能解得p。过程如下：

       

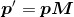
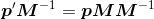 方程两端各乘以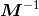

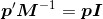根据可逆矩阵的定义，有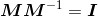

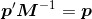根据单位矩阵的定义，有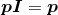

在任何一本大学水平的线性代数教科书里，都可以找到求逆矩阵公式的推导过程，这里也就不再赘述了。此公式由原矩阵的伴随矩阵和行列式构成：

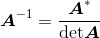
                                                                        （2.6）

例2.10

推导2*2矩阵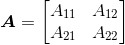的逆矩阵通式，并利用此式求出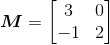矩阵的逆矩阵。

已知

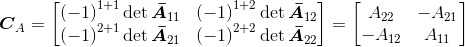
因此，

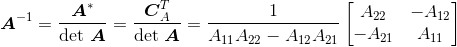
现在运用此公式来求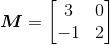矩阵的逆矩阵：

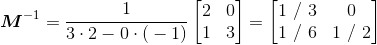
为了核实结果，我们来验证：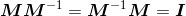

---

注意

对于规模较小的矩阵（4*4及其以下规模的矩阵）来说，运用伴随矩阵的方法将得到不错的计算效率。但针对规模更大的矩阵而言，就要使用诸如高斯消元法（Gaussian elimination，也作高斯消去法）等其他手段。由于我们关注于3D计算机图形学中所涉及的具有特殊形式的矩阵，因此也就提前确定出了它们的求逆矩阵公式。这样一来，我们便无须在求常用的逆矩阵上浪费CPU资源了，继而也就极少会在代码中运用式（2.6）。

---

我们以下列“矩阵乘积的逆”这一实用的代数性质，为此节画上句号：

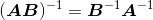
该性质假设矩阵A与矩阵B都是可逆的，而且皆为同维方阵。为了证明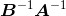是乘积AB的逆，我们必须证实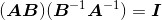以及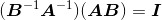。证明过程如下：

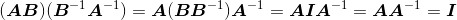
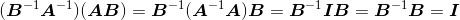
2.8　用DirectXMath库处理矩阵

为了对点与向量进行变换，就要借助1*4行向量以及4*4矩阵。相关原因将在下一章中细述。目前，我们只需把注意力集中在DirectXMath库中常用于表示4*4矩阵的数据类型。

2.8.1　矩阵类型

DirectXMath以定义在DirectXMath.h头文件中的XMMATRIX类来表示4*4矩阵：

#ifdef _XM_NO_INTRINSICS_
    struct XMMATRIX
#else
    XM_ALIGNED_STRUCT(16) XMMATRIX
#endif
    {
#ifdef _XM_NO_INTRINSICS_
        union
        {
            XMVECTOR r[4];
            struct
            {
                float _11, _12, _13, _14;
                float _21, _22, _23, _24;
                float _31, _32, _33, _34;
                float _41, _42, _43, _44;
            };
            float m[4][4];
        };
#else
        XMVECTOR r[4];
#endif

        XMMATRIX() = default;

        XMMATRIX(const XMMATRIX&) = default;

#if defined(_MSC_VER) && (_MSC_FULL_VER < 191426431)
        XMMATRIX& operator= (const XMMATRIX& M) noexcept { r[0] = M.r[0]; r[1] = M.r[1]; r[2] = M.r[2]; r[3] = M.r[3]; return *this; }
#else
        XMMATRIX& operator=(const XMMATRIX&) = default;

        XMMATRIX(XMMATRIX&&) = default;
        XMMATRIX& operator=(XMMATRIX&&) = default;
#endif

        constexpr XMMATRIX(FXMVECTOR R0, FXMVECTOR R1, FXMVECTOR R2, CXMVECTOR R3) noexcept : r{ R0,R1,R2,R3 } {}
        XMMATRIX(float m00, float m01, float m02, float m03,
            float m10, float m11, float m12, float m13,
            float m20, float m21, float m22, float m23,
            float m30, float m31, float m32, float m33) noexcept;
        explicit XMMATRIX(_In_reads_(16) const float* pArray) noexcept;

#ifdef _XM_NO_INTRINSICS_
        float       operator() (size_t Row, size_t Column) const noexcept { return m[Row][Column]; }
        float& operator() (size_t Row, size_t Column) noexcept { return m[Row][Column]; }
#endif

        XMMATRIX    operator+ () const noexcept { return *this; }
        XMMATRIX    operator- () const noexcept;

        XMMATRIX&   XM_CALLCONV     operator+= (FXMMATRIX M) noexcept;
        XMMATRIX&   XM_CALLCONV     operator-= (FXMMATRIX M) noexcept;
        XMMATRIX&   XM_CALLCONV     operator*= (FXMMATRIX M) noexcept;
        XMMATRIX&   operator*= (float S) noexcept;
        XMMATRIX&   operator/= (float S) noexcept;

        XMMATRIX    XM_CALLCONV     operator+ (FXMMATRIX M) const noexcept;
        XMMATRIX    XM_CALLCONV     operator- (FXMMATRIX M) const noexcept;
        XMMATRIX    XM_CALLCONV     operator* (FXMMATRIX M) const noexcept;
        XMMATRIX    operator* (float S) const noexcept;
        XMMATRIX    operator/ (float S) const noexcept;

        friend XMMATRIX     XM_CALLCONV     operator* (float S, FXMMATRIX M) noexcept;
    };

综上所述，XMMATRIX由4个XMVECTOR实例所构成，并借此来使用SIMD技术。此外，XMMATRIX类还为矩阵计算提供了多种重载运算符。

除了各种构造方法之外，还可以使用XMMatrixSet函数来创建XMMATRIX实例：

XMMATRIX XM_CALLCONV XMMatrixSet(  
float m00, float m01, float m02, float m03,  
float m10, float m11, float m12, float m13,  
float m20, float m21, float m22, float m23,  
float m30, float m31, float m32, float m33);

就像通过XMFLOAT2 (2D)，XMFLOAT3 (3D)和XMFLOAT4 (4D)来存储类中不同维度的向量一样，DirectXMath文档也建议我们用XMFLOAT4X4来存储类中的矩阵类型数据成员。

 struct XMFLOAT4X4
    {
        union
        {
            struct
            {
                float _11, _12, _13, _14;
                float _21, _22, _23, _24;
                float _31, _32, _33, _34;
                float _41, _42, _43, _44;
            };
            float m[4][4];
        };

        XMFLOAT4X4() = default;

        XMFLOAT4X4(const XMFLOAT4X4&) = default;
        XMFLOAT4X4& operator=(const XMFLOAT4X4&) = default;

        XMFLOAT4X4(XMFLOAT4X4&&) = default;
        XMFLOAT4X4& operator=(XMFLOAT4X4&&) = default;

        constexpr XMFLOAT4X4(float m00, float m01, float m02, float m03,
            float m10, float m11, float m12, float m13,
            float m20, float m21, float m22, float m23,
            float m30, float m31, float m32, float m33) noexcept
            : _11(m00), _12(m01), _13(m02), _14(m03),
            _21(m10), _22(m11), _23(m12), _24(m13),
            _31(m20), _32(m21), _33(m22), _34(m23),
            _41(m30), _42(m31), _43(m32), _44(m33) {}
        explicit XMFLOAT4X4(_In_reads_(16) const float* pArray) noexcept;

        float       operator() (size_t Row, size_t Column) const noexcept { return m[Row][Column]; }
        float& operator() (size_t Row, size_t Column) noexcept { return m[Row][Column]; }
    };

通过下列方法将数据从XMFLOAT4X4内加载到XMMATRIX中：

inline XMMATRIX XM_CALLCONVXMLoadFloat4x4(const XMFLOAT4X4* pSource);

通过下列方法将数据从XMMATRIX内存储到XMFLOAT4X4中：

inline void XM_CALLCONVXMStoreFloat4x4(XMFLOAT4X4* pDestination, FXMMATRIX M);

2.8.2　矩阵函数

DirectXMath库包含了下列与矩阵相关的实用函数：

XMMATRIX XM_CALLCONV XMMatrixIdentity();   // 返回单位矩阵I
bool XM_CALLCONV XMMatrixIsIdentity(FXMMATRIX M);// 如果M是单位矩阵则返回true
MXMMATRIX XM_CALLCONV XMMatrixMultiply(FXMMATRIX A, CXMMATRIX B);// 返回矩阵乘积AB
BXMMATRIX XM_CALLCONV XMMatrixTranspose(FXMMATRIX M);// 返回MT
MXMVECTOR XM_CALLCONV XMMatrixDeterminant(FXMMATRIX M);// 返回(det M, det M, det M, det M)                           
MXMMATRIX XM_CALLCONV XMMatrixInverse(XMVECTOR* pDeterminant,FXMMATRIX M);// 返回M-1    

在声明具有XMMATRIX参数的函数时，除了要注意1个XMMATRIX应计作4个XMVECTOR参数这一点之外，其他的规则与传入XMVECTOR类型的参数时（见1.6.3节）相一致。假设传入函数的FXMVECTOR参数不超过两个，则第一个XMMATRIX参数应当为FXMMATRIX类型，其余的XMMATRIX参数均应为CXMMATRIX类型。下面的代码展示了在32位Windows平台和编译器（编译器需支持__fastcall以及新增的__vectorcall调用约定）的环境下，这些类型的定义：

// 在32位的Windows系统上，__fastcall调用约定通过寄存器传递前3个XMVECTOR参数，其余的//参数则存在堆栈上
typedef const XMMATRIX& FXMMATRIX;
typedef const XMMATRIX& CXMMATRIX;
// 在32位的Windows系统上，__vectorcall调用约定通过寄存器传递前 6个 XMVECTOR实参，其余的
// 参数则存在堆栈上
typedef const XMMATRIX FXMMATRIX;
typedef const XMMATRIX& CXMMATRIX;

可以看出，在32位Windows操作系统上的__fastcall调用约定中，XMMATRIX类型的参数是不能传至SSE/SSE2寄存器的，因为这些寄存器此时只支持3个XMVECTOR参数传入。而XMMATRIX参数却是由4个XMVECTOR构成，所以矩阵类型的数据只能通过堆栈来加以引用。至于这些类型在其他平台上的定义详情，可见DirectXMath文档[DirectXMath]中“Library Internals”（库的内部细节）下的“Calling Conventions”（调用约定）部分。构造函数方法对于这些规则来说是一个特例。[DirectXMath]建议用户总是在构造函数中采用CXMMATRIX类型来获取XMMATRIX参数，而且对于构造函数也不要使用XM_CALLCONV约定注解。

2.8.3　DirectXMath矩阵示例程序

下列代码提供了一些XMMATRIX类的使用范例，其中包括了上一小节中介绍的大多数函数。

#include <windows.h> // for XMVerifyCPUSupport
#include <DirectXMath.h>
#include <DirectXPackedVector.h>
#include <iostream>
using namespace std;
using namespace DirectX;
using namespace DirectX::PackedVector;

// Overload the  "<<" operators so that we can use cout to 
// output XMVECTOR and XMMATRIX objects.
ostream& XM_CALLCONV operator << (ostream& os, FXMVECTOR v)
{
    XMFLOAT4 dest;
    XMStoreFloat4(&dest, v);

    os << "(" << dest.x << ", " << dest.y << ", " << dest.z << ", " << dest.w << ")";
    return os;
}

ostream& XM_CALLCONV operator << (ostream& os, FXMMATRIX m)
{
    for (int i = 0; i < 4; ++i)
    {
        os << XMVectorGetX(m.r[i]) << "\t";
        os << XMVectorGetY(m.r[i]) << "\t";
        os << XMVectorGetZ(m.r[i]) << "\t";
        os << XMVectorGetW(m.r[i]);
        os << endl;
    }
    return os;
}

int main()
{
    // Check support for SSE2 (Pentium4, AMD K8, and above).
    if (!XMVerifyCPUSupport())
    {
        cout << "directx math not supported" << endl;
        return 0;
    }

    XMMATRIX A(1.0f, 0.0f, 0.0f, 0.0f,
        0.0f, 2.0f, 0.0f, 0.0f,
        0.0f, 0.0f, 4.0f, 0.0f,
        1.0f, 2.0f, 3.0f, 1.0f);

    XMMATRIX B = XMMatrixIdentity();

    XMMATRIX C = A * B;

    XMMATRIX D = XMMatrixTranspose(A);

    XMVECTOR det = XMMatrixDeterminant(A);
    XMMATRIX E = XMMatrixInverse(&det, A);

    XMMATRIX F = A * E;

    cout << "A = " << endl << A << endl;
    cout << "B = " << endl << B << endl;
    cout << "C = A*B = " << endl << C << endl;
    cout << "D = transpose(A) = " << endl << D << endl;
    cout << "det = determinant(A) = " << det << endl << endl;
    cout << "E = inverse(A) = " << endl << E << endl;
    cout << "F = A*E = " << endl << F << endl;
 
    return 0;
}

上述范例程序的输出结果如图2-1所示。

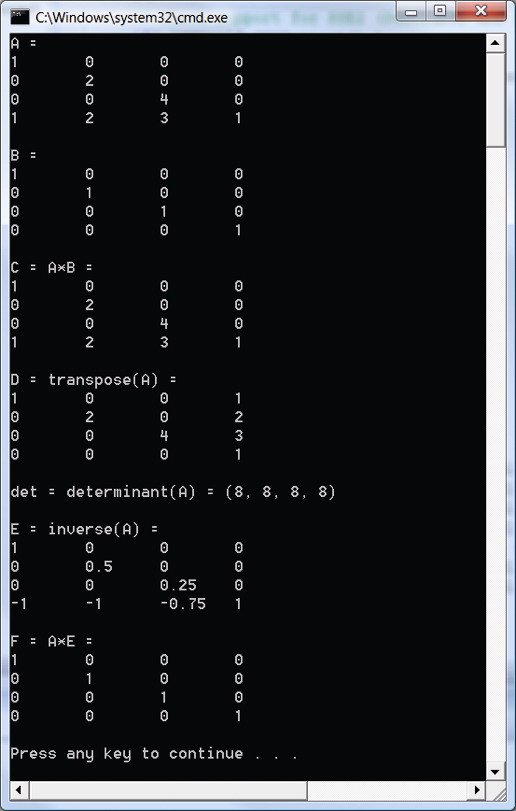
图2-1　范例程序输出的结果