c++之二叉树的递归实现与递归遍历

最新推荐文章于 2024-08-16 20:34:10 发布

原创最新推荐文章于 2024-08-16 20:34:10 发布 · 504 阅读

1 ·

CC 4.0 BY-SA版权

本文介绍了一个使用模板类实现的二叉树数据结构，包括二叉树节点的定义，以及如何创建二叉树并进行前序、中序和后序遍历。通过示例代码展示了二叉树的创建过程和三种遍历方式的具体实现。

CreateBinaryTree.h

template<class T> class BinaryTree;

template<class T> 
class BinTreeNode
{
	friend class BinaryTree<T>;
	T data;
	BinTreeNode *lchild;
	BinTreeNode *rchild;
};

template<class T>
class BinaryTree
{
public:
	BinaryTree(){ root = 0; };//

	void CreateTree();//创建(按照前序规则)
	void CreateTree(BinTreeNode<T> *&currentnode);

	void PreOrder();//前序
	void PreOrder(BinTreeNode<T> *&currentnode);

	void InOrder();//中序
	void InOrder(BinTreeNode<T> *&currentnode);

	void PostOrder();//后序
	void PostOrder(BinTreeNode<T> *&currentnode);

private:
	BinTreeNode<T> *root;
};

template<class T>
void BinaryTree<T>::CreateTree()
{
	CreateTree(root);
}
template<class T>
void BinaryTree<T>::CreateTree(BinTreeNode<T> *&currentnode)
{
	char ch;
	if ((ch = getchar()) == '#')
	{
		currentnode = 0;
	}
	else
	{
		currentnode = new BinTreeNode<T>();
		currentnode->data = ch;
		CreateTree(currentnode->lchild);
		CreateTree(currentnode->rchild);
	}
}

template<class T>
void BinaryTree<T>::PreOrder()
{
	cout << "前序遍历（根-左-右）为";
	PreOrder(root);
}
template<class T>
void BinaryTree<T>::PreOrder(BinTreeNode<T> *&currentnode)
{
	if (currentnode)
	{
		cout << currentnode->data << ' ';
		PreOrder(currentnode->lchild);
		PreOrder(currentnode->rchild);
	}
}

template<class T>
void BinaryTree<T>::InOrder()
{
	cout << "中序遍历（左-根-右）为";
		InOrder(root);
}
template<class T>
void BinaryTree<T>::InOrder(BinTreeNode<T> *&currentnode)
{
	if (currentnode)
	{
		InOrder(currentnode->lchild);
		cout << currentnode->data << ' ';
		InOrder(currentnode->rchild);
	}
}

template<class T>
void BinaryTree<T>::PostOrder()
{
	cout << "后序遍历（左-右-根）为";
		PostOrder(root);
}
template<class T>
void BinaryTree<T>::PostOrder(BinTreeNode<T> *&currentnode)
{
	if (currentnode)
	{
		PostOrder(currentnode->lchild);
		PostOrder(currentnode->rchild);
		cout << currentnode->data << ' ';
	}
}

main.cpp

#include "CreateBinaryTree.h"
#include <iostream>
using namespace std;

int main()
{
	BinaryTree<char> Tree1;
	Tree1.CreateTree();
	Tree1.PreOrder();
	cout << endl;
	Tree1.InOrder();
	cout << endl;
	Tree1.PostOrder();
	cout << endl;
	system("pause");
	return 0;
}

结果为：
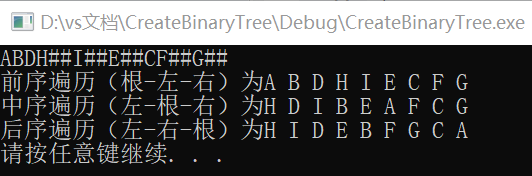
在这里插入图片描述