二叉树
和表、栈、队列等线性数据结构不同,树不是线性的。并且在处理较多的数据时,使用线性结构较慢,而使用树结构则可以提高处理速度。
三种遍历二叉树的方式:先序遍历、中序遍历、后序遍历
- 先序遍历:如果二叉树不为空,则访问根节点,然后访问左子树,最后访问右子树;否则,程序退出。
- 中序遍历:如果二叉树不为空,则先访问左子树,然后访问根节点,最后访问右子树;否则,程序退出。
- 后序遍历:如果二叉树不为空,则先访问左子树,然后访问右子树,最后访问根节点;否则,程序退出。
python程序示例
class BTree:
def __init__(self,value):
self.data = value
self.left = None
self.right = None
# 向左子树插入节点
def insertLeft(self,value):
self.left = BTree(value)
return self.left
# 向右子树插入节点
def insertRight(self,value):
self.right = BTree(value)
return self.right
# 输出节点数据
def show(self):
print(self.data)
# 先序遍历
def preOrder(node):
if node.data:
node.show()
if node.left:
preOrder(node.left)
if node.right:
preOrder(node.right)
# 中序遍历
def midOrder(node):
if node.data:
if node.left:
midOrder(node.left)
node.show()
if node.right:
midOrder(node.right)
# 后序遍历
def postOrder(node):
if node.data:
if node.left:
postOrder(node.left)
if node.right:
postOrder(node.right)
node.show()
'''
主程序
'''
if __name__=='__main__':
Root = BTree('Root') # 构建树
A = Root.insertLeft('A')
C = A.insertLeft('C')
D = A.insertRight('D')
F = D.insertLeft('F')
G = D.insertRight('G')
B = Root.insertRight('B')
E =B.insertRight('E')
print('*************************')
print('Binary Tree pre-traversal')
preOrder(Root)
print('*************************')
print('Binary Tree mid-traversal')
midOrder(Root)
print('*************************')
print('Binary Tree post-traversal')
postOrder(Root)
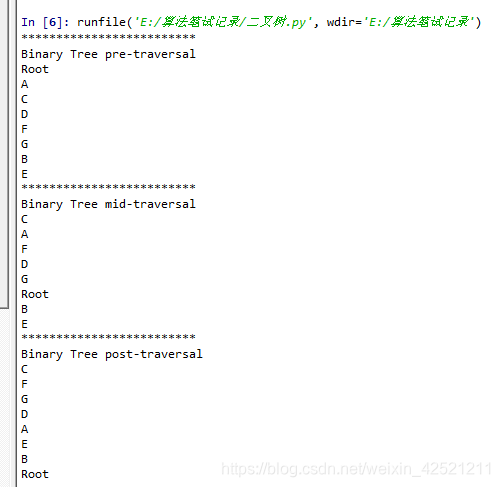
程序输出:
题外记
二叉树的遍历,是递归非常好的一个示例!

























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










