z变换判断稳定性和因果性_动态系统的稳定性分析

稳定性是指在系统受到外界扰动偏离原来的平衡状态，扰动消失后能否回到原来的平衡态的性能，是系统本身所固有的性质。关于稳定性理论，主要有以下一些概念，为了能更好的理解与区分，本文通过参考资料做了总结。

在介绍稳定性理论之前，先要了解什么是平衡态：

极点是影响系统稳定性的重要因素，我们知道极点只在左半平面才会稳定，但是为什么呢？我的理解是，根据拉氏反变换可以变换到时域下的表达式，指数项的指数小于零才能保证状态是稳定的，否则将不稳定，指数函数会随着t增大而发散。举个例子如下:

假设有如上系统，根据计算可以得出该系统极点分别为-1 -2，经过拉氏反变换计算系统的解

可以看到，如果极点满足在左半平面，那么指数项将是收敛的，系统是稳定的。

在经典控制理论当中，可根据系统极点是否在左半平面、赫尔维茨判据、劳斯判据、奈奎斯特判据等进行稳定性分析。现代控制理论当中，采用状态空间描述MIMO线性时变或非线性系统。

1 稳定性基本概念

1.1 BIBO稳定

单输入单输出的线性定常系统， 它的输入、 输出之间的关系可用传递函数表示， 也可通过脉冲响应函数表示。 故系统的输入、 输出特性也可以通过传递函数和脉冲响应函数来研究。

若所有的有界输入引起的零状态响应的输出是有界的。 则称系统为有界输入有界输出稳定，或简称BIBO稳定。其判别方法如下:

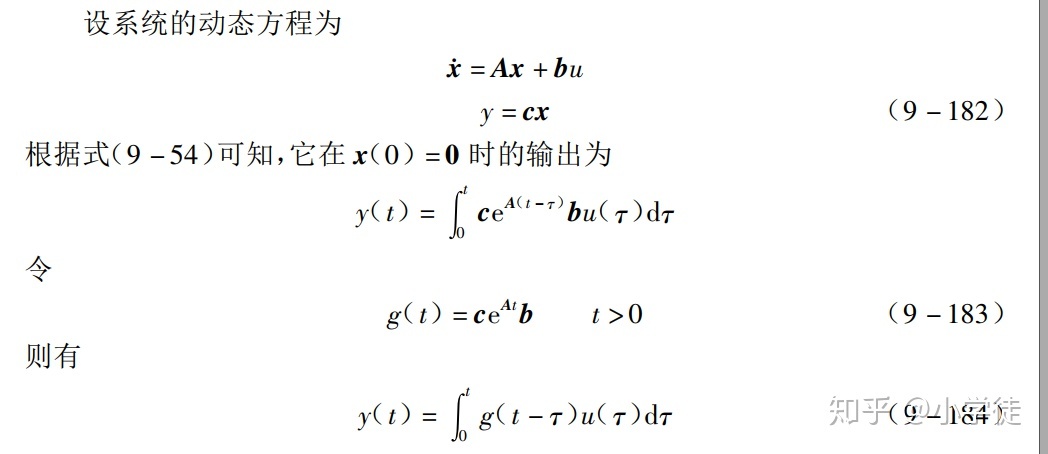
当系统用传递函数g（s）描述时， 系统BIBO 稳定的充分必要条件为：g（s） 的极点具有负实部。

而极点的判定方法，则又回到了上述所介绍的内容。

1.2 Lyapunov稳定：

李氏稳定

与渐近稳定不同的是，状态不一定趋近于平衡点，只约束在某一个范围内。

1.3 渐近稳定

如果系统状态开始在平衡点附近，则系统不会振荡，其状态轨线最终会落在平衡点。但这只是在一定范围内的稳定，也称为局部稳定。

渐近稳定

1.4 全局稳定

2 稳定性判别方法

2.1 Lyapunov第一法

又称间接法，这种方法是通过求解系数矩阵A的特征值(极点)来判断

2.2 Lyapunov第二法

李雅普诺夫第二方法是通过构造李雅普诺夫函数来直接判断运动稳定性的一种定性的方法。由于这种方法没有求出微分方程的解， 而直接研究方程解的稳定性， 因此又称为直接法， 目前它仍然是研究系统（ 包括时变、非线性） 稳定性的有力工具，核心是构造一个标量函数V (x) 作为虚构的广义能量函数（称为 Lyapunov 函数）。定理如下

需要区分的是什么时候临界稳定、什么时候渐近稳定、什么时候全局稳定。关于负定与半负定需要注意的是不包括x=0的情况，也就是说除了原点以外，V是否还有0解。